Понимание, как вычислить периметр по диагонали, может быть полезным при работе с геометрическими фигурами. Зная диагональ, можно узнать полный размер фигуры без необходимости измерять все стороны отдельно. Существует несколько эффективных методов и техник расчета периметра по диагонали, которые упрощают задачу и экономят время.
Первый способ - использование теоремы Пифагора. Если известны длины двух катетов прямоугольного треугольника, то можно вычислить гипотенузу, которая является диагональю фигуры. Затем, по формуле периметра треугольника, можно найти все стороны и их сумму.
Второй способ - расчет периметра квадрата. Если дана диагональ квадрата, то можно использовать соотношение между стороной и диагональю. Для этого нужно умножить длину диагонали на коэффициент, равный корню квадратному из двух. Полученное значение будет являться длиной стороны. После этого умножаем на 4 и получаем периметр квадрата.
Третий способ - вычисление периметра прямоугольника. Если известна диагональ прямоугольника и соотношение между сторонами (например, вид сечения), можно использовать формулу, основанную на теореме Пифагора. Необходимо выразить одну из сторон через диагональ и другую сторону. Затем, используя формулу периметра прямоугольника, можно вычислить периметр фигуры.
Четвертый способ - расчет периметра треугольника по его высоте и основанию. Если известна диагональ и высота треугольника, можно выразить основание через диагональ и высоту. Затем, используя формулу периметра треугольника, можно найти периметр по диагонали.
В завершение, знание этих четырех способов вычисления периметра по диагонали даст возможность значительно упростить работу с геометрическими фигурами и сэкономить время на измерениях, без потери точности результатов.
Вычисление периметра по диагонали с использованием теоремы Пифагора: основные практические методы
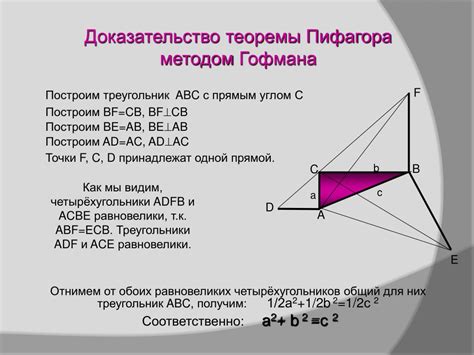
Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: a^2 + b^2 = c^2, где a и b - катеты, c - гипотенуза.
При вычислении периметра по диагонали, мы можем использовать теорему Пифагора для определения сторон треугольника, образованного диагональю и сторонами фигуры.
Основным практическим методом является следующий алгоритм:
- Определить длину диагонали (с).
- Найти длину одной из сторон треугольника (a или b).
- Вычислить длину другой стороны треугольника (a или b) по формуле a^2 + b^2 = c^2.
- Найти длину оставшейся стороны треугольника (c - диагональ).
- Вычислить периметр фигуры по формуле P = a + b + c.
Применение этого метода позволяет вычислить периметр фигуры по её диагонали без необходимости знания всех сторон. Это особенно полезно, когда в задаче известна только диагональ фигуры.
Пример использования:
Пусть у нас есть прямоугольник с известной диагональю длиной 10 единиц. Чтобы вычислить его периметр, мы можем использовать теорему Пифагора.
Используя формулу a^2 + b^2 = c^2, мы можем найти длину одной из сторон треугольника, образованного диагональю и сторонами прямоугольника.
Предположим, что одна из сторон (а) равна 6 единиц. Тогда, используя формулу, мы можем найти длину другой стороны (b): b^2 = c^2 - a^2 = 10^2 - 6^2 = 100 - 36 = 64. Таким образом, b = √64 = 8 единиц.
Длина оставшейся стороны (c) равна диагонали и составляет 10 единиц.
Теперь, используя формулу P = a + b + c, мы можем вычислить периметр прямоугольника: P = 6 + 8 + 10 = 24 единиц.
Таким образом, мы получили значение периметра прямоугольника по его диагонали.
Вычисление периметра по диагонали с использованием теоремы Пифагора является эффективным методом, позволяющим определить периметр геометрической фигуры по диагонали и одной из её сторон. Практический алгоритм на основе этой теоремы позволяет вычислить периметр без знания всех сторон фигуры. Этот метод особенно полезен, когда задача требует определения периметра по диагонали.
Использование тригонометрических соотношений для точного расчета периметра по диагонали
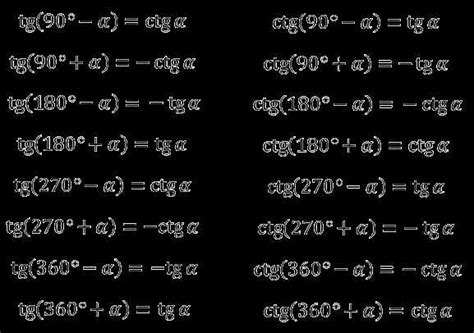
Расчет периметра по диагонали может быть сложной задачей, особенно если известны только длины сторон фигуры. Однако с использованием некоторых тригонометрических соотношений можно точно определить периметр, основываясь только на известных диагоналях.
Тригонометрические соотношения позволяют связать длины сторон и углы в фигуре. Существует несколько формул, которые помогают рассчитать периметр исходя из заданных диагоналей. Например, для прямоугольника можно использовать следующую формулу:
Периметр = 2 * (a + b),
где a и b - длины сторон прямоугольника.
Если же известны диагонали, то с помощью тригонометрических соотношений можно рассчитать длину стороны. Например, для прямоугольника с известными диагоналями d1 и d2 можно использовать следующую формулу:
Периметр = 2 * (d1 * sin(α) + d2 * cos(α)),
где α - угол между диагоналями.
Тригонометрические соотношения позволяют расчитать периметр не только для прямоугольника, но и для других геометрических фигур, таких как треугольник, ромб и трапеция. Основываясь на известных диагоналях, можно использовать соответствующие формулы, чтобы получить точные значения периметра.
Примечание: При использовании тригонометрических соотношений необходимо учитывать единицы измерения длин. Для получения правильных результатов все длины должны быть измерены в одних и тех же единицах.
Применение геометрических преобразований и формул для быстрого и эффективного определения периметра по диагонали

Определение периметра многоугольника, используя только длину его диагонали, может быть сложной задачей. Однако, с использованием геометрических преобразований и формул, можно существенно упростить этот процесс и получить точный результат.
Во-первых, для того чтобы определить периметр многоугольника по диагонали, необходимо знать количество его сторон. Для простоты рассмотрим случай правильного многоугольника, у которого все стороны равны. В этом случае количество сторон многоугольника можно определить по формуле:
- Количество сторон = Длина диагонали / Длина одной стороны.
Зная количество сторон многоугольника, можно рассчитать периметр по формуле:
- Периметр = Количество сторон * Длина одной стороны.
Когда мы знаем длину диагонали и количество сторон многоугольника, мы можем использовать геометрическое преобразование для определения длины одной стороны. Например, можно воспользоваться формулой:
- Длина одной стороны = Длина диагонали / (2 * sin(π / Количество сторон)).
Таким образом, используя геометрические преобразования и формулы, можно быстро и эффективно вычислить периметр многоугольника по диагонали. Эти методы особенно полезны, когда точные значения сторон многоугольника неизвестны, но имеется информация о длине его диагонали.