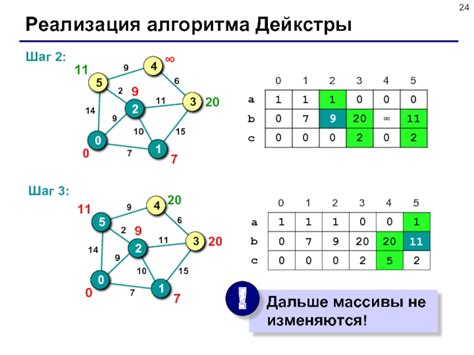
Алгоритм Дейкстры – один из основных алгоритмов в теории графов, который используется для нахождения кратчайших путей от одной вершины до всех остальных вершин во взвешенном графе. Этот алгоритм был придуман голландским ученым Эдсгером Дейкстрой в 1956 году и с тех пор активно применяется в различных областях, связанных с оптимизацией маршрутов.
Идея алгоритма Дейкстры заключается в том, чтобы постепенно находить кратчайшие пути от начальной вершины до всех остальных. Алгоритм работает следующим образом: изначально расстояние до всех вершин, кроме начальной, считается бесконечно большим. Затем, на каждом шаге, выбирается вершина с наименьшим расстоянием и обновляются расстояния до всех соседних вершин, проходящих через выбранную. Процесс продолжается до тех пор, пока все вершины не будут посещены.
Применение алгоритма Дейкстры разнообразно: от нахождения оптимального маршрута в GPS-навигаторах до планирования трафика в сетях связи. Многие алгоритмы обхода графов и оптимизации маршрутов в своей работе используют алгоритм Дейкстры или его модификации. Проанализировать его шаги и понять его логику поможет изучение примеров с подробными пошаговыми объяснениями.
Алгоритм Дейкстры: рассмотрим его шаг за шагом
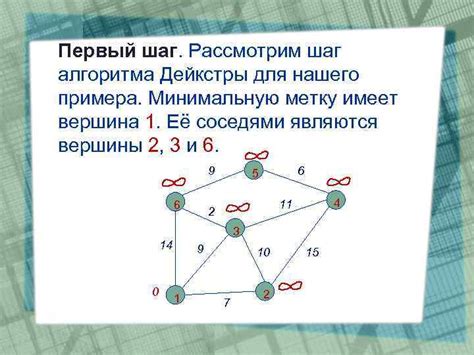
Основная идея алгоритма Дейкстры заключается в постепенном наращивании кратчайшего пути от начальной вершины к остальным. Здесь используется понятие "расстояние" от начальной вершины до всех остальных. Изначально расстояние до начальной вершины равно 0, а до всех остальных - бесконечность.
Алгоритм Дейкстры состоит из нескольких шагов. На каждом шаге выбирается вершина с минимальным расстоянием и проверяются все её соседи. Если расстояние от начальной вершины до соседа меньше, чем текущее расстояние до соседа, то оно обновляется. Процесс повторяется до тех пор, пока все вершины не будут просмотрены.
Используя алгоритм Дейкстры, можно найти кратчайший путь от одной вершины до любой другой во взвешенном графе. Это полезно в таких областях как транспортная логистика, маршрутизация сетей, оптимизация планирования и другие задачи, где необходимо найти оптимальный путь или план действий.
Алгоритм Дейкстры - мощный инструмент для работы с взвешенными графами. Понимание его работы на шагах поможет разобраться с его применением и использовать его для решения сложных задач.
Определение и основные принципы работы
Основная идея алгоритма заключается в пошаговом обновлении длин путей от начальной вершины до остальных вершин. На каждом шаге алгоритм выбирает вершину с наименьшей оценкой, называемой расстоянием, и обновляет оценки для ее соседей. После того как все вершины будут обработаны, будет найдено кратчайшее расстояние от начальной вершины до всех остальных.
Процесс работы алгоритма можно представить в следующих шагах:
- Устанавливаем начальную вершину и задаем ей начальное расстояние 0, а остальным вершинам - бесконечность.
- Помечаем текущую вершину как посещенную и обновляем расстояния до ее соседей, если новое расстояние меньше текущего.
- Выбираем следующую непосещенную вершину с наименьшим расстоянием и повторяем шаг 2.
- Повторяем шаг 3 до тех пор, пока все вершины не будут помечены как посещенные или до тех пор, пока не останется непосещенных вершин с бесконечным расстоянием.
После завершения работы алгоритма, для каждой вершины можно получить кратчайший путь из начальной вершины, пройдя по направлению обновления расстояний.
Использование алгоритма Дейкстры в практических задачах
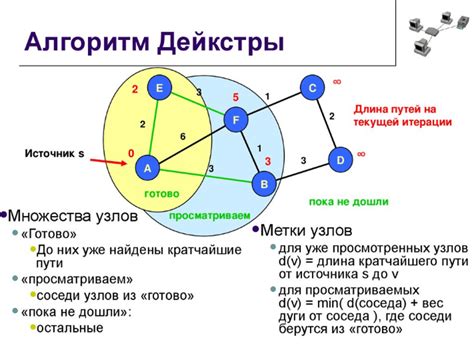
Основная идея алгоритма Дейкстры заключается в том, чтобы постепенно обрабатывать узлы графа, начиная с стартового узла, и находить кратчайшее расстояние до каждого из них. По мере продвижения алгоритма, расстояние до остальных узлов обновляется, если находится более короткий путь. В конечном итоге, алгоритм Дейкстры находит кратчайшие пути от стартового узла ко всем остальным узлам графа.
Применение алгоритма Дейкстры заслуживает внимания во многих сценариях. Например, при планировании маршрута доставки, агенту необходимо найти оптимальный путь для доставки товаров различным клиентам. Алгоритм Дейкстры может быть использован, чтобы найти самый быстрый или наименее затратный путь для доставки.
В сфере сетей связи, алгоритм Дейкстры может быть использован для оптимизации маршрутов передачи данных между коммутаторами и маршрутизаторами. Он позволяет найти наиболее эффективные пути для передачи данных и минимизировать время задержки.
Также, алгоритм Дейкстры может быть применен в планировании транспорта для определения оптимального маршрута для перевозки грузов. Это может помочь максимизировать эффективность транспортной системы и снизить затраты на доставку.
Реализация алгоритма Дейкстры на языке программирования
Для реализации алгоритма Дейкстры на языке программирования существует несколько подходов. Одним из самых простых и понятных способов является использование структуры данных "очередь с приоритетом".
Для начала, необходимо инициализировать массив расстояний до вершин, где значение для стартовой вершины будет равно 0, а для всех остальных - бесконечность. Затем, в верхнем цикле необходимо выбирать вершину с наименьшим расстоянием из очереди с приоритетом и обновлять расстояния до ее соседних вершин, если полученное расстояние меньше текущего значения.
Алгоритм заканчивает свою работу, когда все вершины будут посещены и все их расстояния будут определены. Затем можно вывести полученные кратчайшие пути на экран или использовать их для решения конкретной задачи.
Пример кода на языке программирования Python:
def dijkstra(graph, start):
distances = {v: float('inf') for v in graph} # инициализация расстояний
distances[start] = 0 # расстояние до стартовой вершины равно 0
queue = [start] # очередь с приоритетом
while queue:
current = queue.pop(0)
for neighbor in graph[current]:
distance = distances[current] + graph[current][neighbor]
if distance
В данном примере функция dijkstra() принимает на вход взвешенный ориентированный граф в виде словаря, где ключами являются вершины, а значениями - словари с соседями и соответствующими им весами ребер. Результат работы функции - словарь с кратчайшими путями от стартовой вершины до всех остальных.
Таким образом, реализация алгоритма Дейкстры на языке программирования позволяет находить кратчайшие пути в графе и использовать их для решения различных задач, связанных с поиском оптимального маршрута.
Примеры и приложения алгоритма Дейкстры

Алгоритм Дейкстры широко применяется в различных областях, где требуется нахождение кратчайшего пути в графе с взвешенными ребрами. Ниже приведены несколько примеров и приложений алгоритма Дейкстры:
1. Навигация и маршрутизация:
Алгоритм Дейкстры часто используется в навигационных системах и приложениях для поиска оптимального маршрута от одной точки до другой. Он может помочь в определении самого быстрого или самого экономически выгодного пути, учитывая различные факторы, такие как дорожные условия или стоимость проезда.
2. Телекоммуникации:
В телекоммуникационных сетях, особенно в сетях с коммутацией пакетов, алгоритм Дейкстры может быть использован для определения наименьшего числа переходов или наиболее эффективного потока пакетов между узлами сети. Он позволяет оптимизировать загрузку сети и повысить ее эффективность.
3. Планирование задач:
Алгоритм Дейкстры можно применять для планирования задач и определения наименьших затрат или шагов, необходимых для достижения цели. Например, он может быть использован для оптимизации распределения ресурсов, определения оптимального порядка выполнения задач или для планирования процессов в операционных системах.
4. Игровая теория:
В игровой теории алгоритм Дейкстры может быть применен для моделирования стратегий и определения наиболее выгодных ходов. Он может использоваться в играх с фиксированной или стохастической моделью, помогая определить оптимальные решения и победную стратегию.
Алгоритм Дейкстры является мощным инструментом в области графов и нахождения кратчайших путей. Его широкое применение в различных сферах делает его ключевым компонентом для решения разнообразных задач.