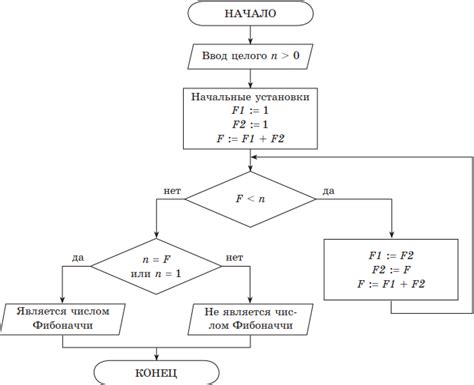
Фибоначчи – это последовательность чисел, где каждое число является суммой двух предыдущих чисел. Этот ряд чисел, известный уже более века, оказывает влияние не только на математику, но и на другие области, такие как компьютерное программирование. Калькулятор Фибоначчи – это небольшая программная функция, которая позволяет вычислить число Фибоначчи для заданного индекса или ряда индексов.
Алгоритм калькулятора Фибоначчи основан на рекурсии и итерации. Рекурсивный подход использует самосходящуюся функцию, которая вызывает себя снова и снова до тех пор, пока не будет достигнуто базовое условие. Итеративный подход, с другой стороны, использует циклы и промежуточные переменные для вычисления чисел Фибоначчи последовательно.
При использовании рекурсивного алгоритма калькулятора Фибоначчи следует быть осторожным с тем, чтобы не вызвать условие бесконечной рекурсии. Вместо этого, важно установить базовое условие, когда функция должна остановиться и вернуть результат. В случае калькулятора Фибоначчи это обычно число 0 или 1. В противном случае, рекурсивные вызовы будут продолжаться до истощения стека вызовов.
Что такое алгоритм Фибоначчи?

| Номер | Число |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 1 |
| 4 | 2 |
| 5 | 3 |
| 6 | 5 |
Алгоритм Фибоначчи может быть использован для решения различных задач. Он может быть использован для генерации чисел Фибоначчи в заданном диапазоне, для нахождения n-го числа Фибоначчи и для проверки, является ли число Фибоначчи или нет.
Реализация алгоритма Фибоначчи обычно основывается на использовании цикла или рекурсии. При использовании цикла, числа Фибоначчи вычисляются и сохраняются по очереди. При использовании рекурсии, функция вызывает саму себя до достижения базового случая.
Алгоритм Фибоначчи широко используется в программировании и вычислительной математике, так как он является простым и эффективным способом генерации чисел, а также имеет множество практических применений в различных областях.
Определение алгоритма калькулятора Фибоначчи
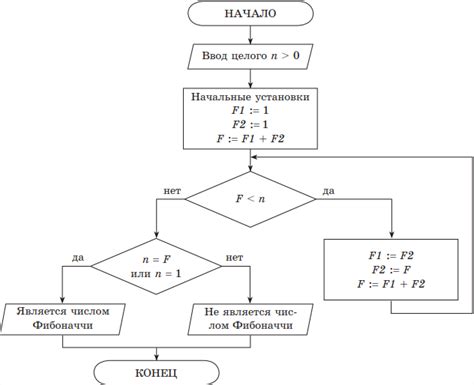
Основная идея алгоритма калькулятора Фибоначчи заключается в использовании рекурсии. Рекурсия - это процесс, в котором функция вызывает сама себя.
Алгоритм начинается с определения базовых случаев - когда порядковый номер равен 0 или 1, возвращается соответствующее значение (0 или 1). Для остальных случаев вызывается функция для вычисления двух предыдущих чисел Фибоначчи, и их сумма возвращается в качестве результата.
Этапы выполнения алгоритма:
- Проверить базовые случаи;
- Вызвать функцию для вычисления двух предыдущих чисел Фибоначчи;
- Вернуть сумму двух предыдущих чисел в качестве результата.
Пример работы алгоритма:
- Вызов функции fib(5):
- 5 не равно 0 и 1, поэтому вызываем функцию fib(4) и fib(3).
- 4 не равно 0 и 1, поэтому вызываем функцию fib(3) и fib(2).
- 3 не равно 0 и 1, поэтому вызываем функцию fib(2) и fib(1).
- 2 не равно 0 и 1, поэтому вызываем функцию fib(1) и fib(0).
- 1 равно 1, поэтому возвращаем 1.
- 0 равно 0, поэтому возвращаем 0.
Алгоритм калькулятора Фибоначчи позволяет находить числа Фибоначчи с использованием рекурсии и базовых случаев. Этот алгоритм может быть использован в различных программных задачах, где требуется вычисление чисел Фибоначчи.
Как работает алгоритм калькулятора Фибоначчи?

Алгоритм работает следующим образом:
- Устанавливается начальное значение двух предыдущих чисел
a = 0иb = 1. - Выполняется цикл, который продолжается до того момента, пока не будет достигнуто нужное количество чисел ряда Фибоначчи или требуемое число.
- В каждой итерации цикла происходит следующее:
- Вычисляется новое число ряда Фибоначчи, как сумма предыдущих двух чисел:
c = a + b. - Предыдущие числа заменяются на новые:
a = bиb = c. - Новое число ряда Фибоначчи добавляется в результат.
- Вычисляется новое число ряда Фибоначчи, как сумма предыдущих двух чисел:
Например, чтобы вычислить первые 10 чисел ряда Фибоначчи, алгоритм будет иметь следующий вид:
a = 0;
b = 1;
result = [];
for (let i = 0; iТаким образом, алгоритм калькулятора Фибоначчи позволяет генерировать числа ряда Фибоначчи, которые могут использоваться в различных задачах, например, для решения задач с оптимизацией, построения графиков, кодирования и многих других.
Примеры использования алгоритма Фибоначчи

Алгоритм Фибоначчи находит широкое применение в различных областях. Ниже приведены несколько примеров его использования:
Финансовая аналитика: Алгоритм Фибоначчи используется для прогнозирования цен на финансовых рынках. С помощью последовательности чисел Фибоначчи можно определить уровни поддержки и сопротивления на графиках цен акций и валютных пар.
Компьютерная графика: Числа Фибоначчи часто используются в компьютерной графике для создания интересных и гармоничных визуальных эффектов, таких как спирали, фракталы и оптические иллюзии.
Криптография: Алгоритм Фибоначчи можно использовать при генерации псевдослучайных чисел, которые имеют широкий спектр применений в криптографии, включая создание криптографических ключей и шифрование данных.
Биология: Числа Фибоначчи встречаются в природе, в феноменах биологии, таких как расположение лепестков на цветах, спирали на раковинах улиток и соотношение размеров ветвей деревьев.
Интернет-технологии: Веб-разработчики могут использовать алгоритм Фибоначчи для оптимизации работы сайтов, например, для определения оптимального размера кэша или установки ограничений на количество запросов к базе данных.
Математика и наука: Числа Фибоначчи имеют множество интересных математических свойств и отношений, которые активно исследуются учеными. Использование алгоритма Фибоначчи позволяет решать разнообразные математические задачи и обнаруживать паттерны и закономерности в числовых последовательностях.
Это лишь небольшой перечень областей, в которых алгоритм Фибоначчи находит применение. Возможности этого алгоритма широки, и его использование может приносить пользу в различных сферах деятельности.
Плюсы и минусы алгоритма калькулятора Фибоначчи

Плюсы:
1. Простота реализации. Алгоритм калькулятора Фибоначчи можно записать в несколько строк кода и легко понять его логику.
2. Быстрое вычисление малых чисел. При вычислении небольших чисел Фибоначчи алгоритм работает быстро и без проблем.
3. Эффективность в случае кэширования. Если предыдущие значения ряда Фибоначчи сохраняются в памяти компьютера, алгоритм может быть эффективным при вычислении больших чисел.
Минусы:
1. Высокая вычислительная сложность. Алгоритм калькулятора Фибоначчи имеет экспоненциальную сложность, что означает, что время выполнения растет быстро с увеличением входного числа.
2. Неэффективность при вычислении больших чисел. При вычислении очень больших чисел Фибоначчи алгоритм становится очень медленным и может потребовать большого количества ресурсов.
3. Потребление памяти. В случае отсутствия кэширования предыдущих значений, алгоритм может потреблять много памяти для хранения временных значений.