Алгоритм нахождения пересечения треугольников на плоскости — подробное руководство для программистов

Пересечение треугольников на плоскости – это важная задача в области компьютерной графики, геометрии и визуализации. В различных областях науки и техники требуется определить, пересекаются ли два треугольника на плоскости и какие точки пересечения образуют.

В данной статье мы представляем вам алгоритм пересечения треугольников на плоскости. Мы подробно рассмотрим все необходимые шаги, чтобы вы могли применить его на практике. Наш алгоритм основан на геометрических принципах и использует точные вычисления координат, векторов и площадей треугольников.

Вам не потребуется быть математиком или программистом, чтобы использовать этот алгоритм. Мы предоставим вам простые инструкции и пошаговое руководство, которые помогут вам в решении задачи. Необходимые формулы и примеры будут сопровождаться подробными объяснениями, чтобы вы могли легко разобраться во всех деталях.

Если вы интересуетесь компьютерной графикой, визуализацией или геометрией, то этот алгоритм станет незаменимым инструментом в вашей работе. Пересечение треугольников имеет широкий спектр применений, от построения 3D-моделей до численного анализа сложных систем. Приготовьтесь к погружению в увлекательный мир пересечения треугольников!

Определение пересечения

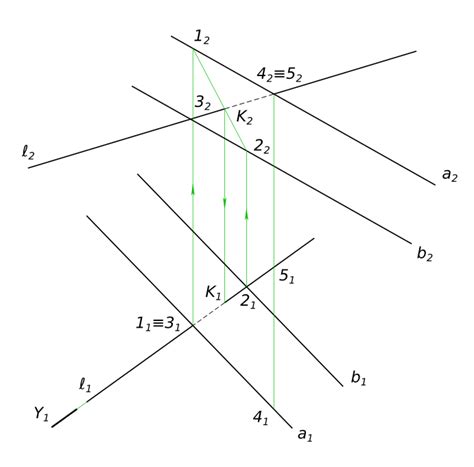
1. Найдите уравнение каждой стороны треугольника в виде прямой на плоскости.
2. Пересеките каждую сторону одного треугольника с каждой стороной другого треугольника, используя уравнения прямых, полученные на предыдущем шаге. Если пересечение происходит, то имеется общая точка.
3. Если общая точка существует хотя бы для одной стороны, то треугольники пересекаются. В противном случае, треугольники не пересекаются.

Таблица ниже показывает пример уравнений прямых для треугольника ABC и DEF:

Если не найдено общих точек при пересечении, то треугольники не пересекаются на плоскости.

Определение точки пересечения треугольников на плоскости

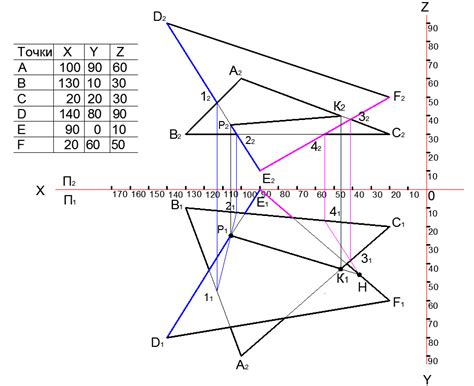
Одним из наиболее популярных алгоритмов является алгоритм Мёллера-Трумбора. Данный алгоритм основывается на вычислении прямоугольников, в которые вписаны треугольники, и нахождении точки пересечения этих прямоугольников. Затем, используя информацию о расположении точек внутри прямоугольников, можно вычислить точку пересечения треугольников.

В таблице ниже приведены шаги алгоритма Мёллера-Трумбора:

Метод нахождения пересекающихся сторон треугольников

Алгоритм пересечения треугольников на плоскости начинается с вычисления всех сторон каждого из треугольников. Далее производится проверка пересечения каждой стороны одного треугольника с каждой стороной другого треугольника.

Для каждой пары сторон треугольников вычисляются коэффициенты уравнений прямых, на которых они лежат. Затем производится проверка условий пересечения этих прямых.

Если найдена пара пересекающихся сторон, можно найти точку пересечения путем решения системы уравнений, составленной из уравнений прямых, на которых лежат пересекающиеся стороны.

Помимо нахождения пересекающихся сторон, алгоритм также учитывает случаи, когда треугольники совпадают или один треугольник содержится внутри другого. В этих случаях также можно найти пересекающиеся стороны, которые совпадают с соответствующими сторонами треугольников.

Важно отметить, что данный алгоритм работает только для треугольников на плоскости и не применим к трехмерным треугольникам или другим геометрическим фигурам.

Примечание: данный алгоритм не был предназначен для работы с вложенными или самопересекающимися треугольниками.

Построение алгоритма

Алгоритм пересечения треугольников на плоскости можно разделить на несколько шагов:

1. Определение координат и параметров треугольников.
2. Проверка на пересечение треугольников.
3. Вычисление точек пересечения, если они есть.
4. Проверка на нахождение точек пересечения внутри треугольников.

Для начала необходимо получить координаты вершин каждого из треугольников. Это может быть сделано как вручную, так и с помощью математических функций или алгоритмов. Для удобства дальнейших вычислений рекомендуется использовать структуры данных, которые позволяют хранить информацию о треугольниках.

Далее следует провести проверку на пересечение треугольников. Для этого можно воспользоваться различными методами, например, проверкой пересечения сторон треугольников или использованием алгоритмов проверки наложения фигур.

Если треугольники пересекаются, необходимо вычислить точки пересечения. Для этого можно воспользоваться геометрическими алгоритмами, такими как поиск точек пересечения прямых и отрезков.

После этого следует проверить, находятся ли точки пересечения внутри треугольников. Для этого можно использовать, например, алгоритм проверки принадлежности точки многоугольнику.

Таким образом, алгоритм пересечения треугольников на плоскости состоит из нескольких этапов, которые позволяют определить наличие пересечения треугольников и вычислить точки пересечения. Этот алгоритм может быть использован в различных сферах, таких как компьютерная графика, трехмерное моделирование и др.

Шаг 1. Определение вершин и сторон треугольников

Для определения вершин треугольника, вам понадобится знать координаты каждой точки, которые образуют его. Например, треугольник может быть определен тремя точками A, B и C, где A(x1, y1), B(x2, y2) и C(x3, y3).

Координаты вершин можно записать в виде векторов:

Вершина A: A(x1, y1) = [x1, y1]

Вершина B: B(x2, y2) = [x2, y2]

Вершина C: C(x3, y3) = [x3, y3]

После определения вершин, стороны треугольника могут быть вычислены. Стороны обычно обозначаются AB, BC и CA.

Для вычисления стороны AB, можно использовать формулу расстояния между двумя точками:

d = sqrt((x2 - x1)^2 + (y2 - y1)^2)

Таким образом, сторона AB будет равна:

AB: AB = [B - A] = [x2 - x1, y2 - y1]

Аналогично, стороны BC и CA могут быть вычислены по формулам:

BC: BC = [C - B] = [x3 - x2, y3 - y2]

CA: CA = [A - C] = [x1 - x3, y1 - y3]

Зная координаты вершин и стороны каждого треугольника, можно переходить к следующему шагу - определению пересечений.