В математике существует несколько способов нахождения вершин треугольника по координатам вектора. Это важная задача, которая может быть использована в различных отраслях, таких как компьютерная графика, геометрия, физика и другие. В этой статье мы рассмотрим один из алгоритмов, который позволяет найти вершины треугольника, зная только координаты вектора.
Прежде чем перейти к самому алгоритму, давайте кратко разберемся, что такое вектор и треугольник. Вектор - это математический объект, который характеризуется направлением и длиной. Он может быть представлен с помощью координат, которые указывают на его начальную и конечную точки. Треугольник - это геометрическая фигура, образованная тремя сторонами, которые соединяют вершины. Каждая вершина треугольника может быть задана координатами вектора.
Теперь перейдем к алгоритму. Для нахождения вершин треугольника по координатам вектора мы можем воспользоваться следующей формулой:
вершина = начальная точка + (координаты вектора * длина стороны)
где начальная точка - это координаты первой вершины треугольника, координаты вектора - это величины, указывающие направление и длину вектора, и длина стороны - это длина соответствующей стороны треугольника.
Вектор и его координаты: определение и свойства
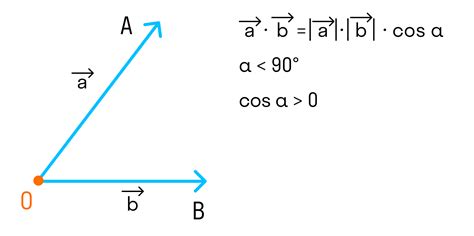
Координаты вектора – числовые значения, которые определяют положение вектора на координатной плоскости. В двумерном пространстве вектор может быть представлен двумя координатами – (x, y), где x – горизонтальная координата, а y – вертикальная координата.
Свойства вектора:
- Длина: Длиной вектора называется величина, равная расстоянию между его началом и концом. Длину можно вычислить с помощью теоремы Пифагора или с помощью формулы d = sqrt(x^2 + y^2), где d – длина вектора, x – горизонтальная координата, а y – вертикальная координата.
- Направление: Направление вектора определяется углом, под которым он отложен относительно начала координат. Угол может быть измерен в градусах или радианах.
- Сложение: Векторы могут быть сложены путем сложения их соответствующих координат. Если у нас есть два вектора (a, b) и (c, d), то их сумма будет равна вектору (a+c, b+d).
- Умножение на скаляр: Умножение вектора на скаляр приводит к изменению его длины и ориентации. Если у нас есть вектор (a, b) и скаляр k, то умножение будет равно вектору (ka, kb).
Зная координаты вектора, мы можем с легкостью вычислить его длину, определить его направление и производить арифметические операции над ним. Основные свойства вектора делают его незаменимым инструментом в математике и физике.
Треугольник: определение и характеристики

У треугольника есть несколько характеристик:
- Стороны треугольника: каждая сторона обозначается маленькой буквой и параметризуется длиной отрезка между двумя вершинами.
- Углы треугольника: каждый угол обозначается заглавной буквой и измеряется в градусах. Сумма трех углов треугольника всегда равна 180 градусам.
- Высоты треугольника: каждая высота обозначается двумя вершинами, между которыми она проведена, и измеряется в длине отрезка от одной вершины до прямоугольной проекции остальной вершины на сторону треугольника.
- Медианы треугольника: каждая медиана проходит через одну из вершин и середины противоположной стороны треугольника, разделяя ее на две равные части.
- Биссектрисы треугольника: каждая биссектриса проходит через одну из вершин и делит соответствующий угол на два равных угла.
- Окружность, вписанная в треугольник: окружность, которая касается всех трех сторон треугольника и называется вписанной окружностью.
- Окружность, описанная вокруг треугольника: окружность, проходящая через все три вершины треугольника и называется описанной окружностью.
Знание характеристик треугольника помогает в анализе и решении геометрических задач, алгоритмах и программировании.
Координаты вектора треугольника: вычисление и примеры
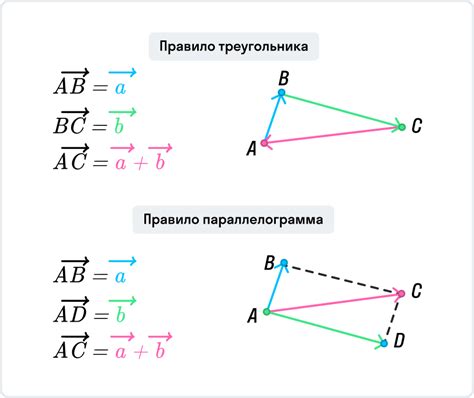
Для вычисления координат вершин треугольника по координатам вектора можно использовать такой алгоритм:
| Шаг | Действие |
|---|---|
| 1 | Задать координаты одной из вершин треугольника (например, A). |
| 2 | Рассчитать векторы AB и AC, где B и C - остальные вершины треугольника. |
| 3 | Найти координаты вершины B с помощью формулы B = A + AB. |
| 4 | Аналогично, найти координаты вершины C с помощью формулы C = A + AC. |
Возьмем пример. Имеется треугольник ABC, где A(1, 2), вектор AB(2, 3) и вектор AC(4, 1). Применяя алгоритм, можно вычислить координаты вершин треугольника:
- Задаем A(1, 2).
- Рассчитываем векторы AB(2, 3) и AC(4, 1).
- Находим B = A + AB = (1, 2) + (2, 3) = (3, 5).
- Находим C = A + AC = (1, 2) + (4, 1) = (5, 3).
Таким образом, получаем координаты вершин треугольника: A(1, 2), B(3, 5), C(5, 3).
Вычисление координат вектора треугольника с помощью описанного алгоритма позволяет удобно оперировать геометрическими объектами и использовать полученные значения при решении различных задач.
Алгоритм нахождения вершин треугольника по координатам вектора
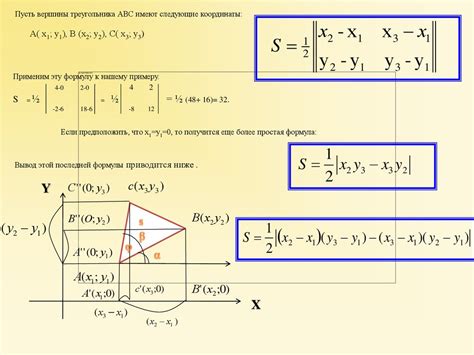
Теория
Для нахождения вершин треугольника по координатам вектора можно использовать следующий алгоритм:
- Взять вектор, для которого известны координаты вершин треугольника.
- Определить длины сторон треугольника, используя формулу расстояния между двумя точками в декартовой системе координат.
- Найти углы треугольника, используя теорему косинусов.
- Используя найденные длины и углы, вычислить координаты остальных двух вершин треугольника.
Существуют различные способы решения этой задачи, в зависимости от условий и векторов, которые уже известны.
Пример
Предположим, у нас есть известные вершины треугольника: A(2, 3), B(6, 7) и C(8, 1). Необходимо найти координаты остальных двух вершин треугольника.
Шаг 1: Взять вектор AB. Его координаты будут (6-2, 7-3) = (4, 4).
Шаг 2: Вычислить длины сторон треугольника.
- Длина стороны AB = √((4^2) + (4^2)) = √(16 + 16) = √32 ≈ 5.657
- Длина стороны AC = √((6^2) + (2^2)) = √(36 + 4) = √40 ≈ 6.325
- Длина стороны BC = √((2^2) + (6^2)) = √(4 + 36) = √40 ≈ 6.325
Шаг 3: Найти углы треугольника ABC.
- Угол A = arccos((5.657^2 + 6.325^2 - 6.325^2) / (2 * 5.657 * 6.325)) ≈ 0.918 радиан ≈ 52.62 градуса
- Угол B = arccos((5.657^2 + 6.325^2 - 5.657^2) / (2 * 5.657 * 6.325)) ≈ 1.166 радиан ≈ 66.77 градуса
- Угол C = 180 - 52.62 - 66.77 ≈ 60.61 градуса
Шаг 4: Используя найденные длины и углы, вычислить координаты остальных двух вершин треугольника.
- Координаты вершины D: x = 2 + 5.657 * cos(52.62), y = 3 + 5.657 * sin(52.62)
- Координаты вершины E: x = 2 + 6.325 * cos(180 - 66.77), y = 3 + 6.325 * sin(180 - 66.77)
Таким образом, мы можем найти координаты вершин треугольника, используя данную методику.
Шаг 1: вычисление длины сторон треугольника
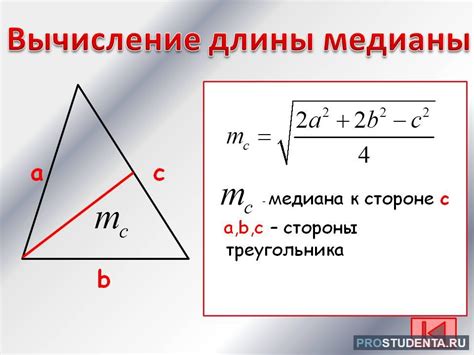
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В нашем случае, треугольник может быть произвольным, поэтому мы должны использовать общую формулу для нахождения длины сторон треугольника:
Для стороны AB с координатами (x1, y1) и (x2, y2) длина может быть вычислена следующим образом:
- Вычисляем разницу между x-координатами: dx = x2 - x1
- Вычисляем разницу между y-координатами: dy = y2 - y1
- Вычисляем квадрат разницы по x: dx_square = dx * dx
- Вычисляем квадрат разницы по y: dy_square = dy * dy
- Вычисляем сумму квадратов разниц: sum_squares = dx_square + dy_square
- Находим квадратный корень от суммы квадратов: length = sqrt(sum_squares)
Повторяем этот процесс для каждой пары вершин треугольника, чтобы найти длины всех трех сторон.
Шаг 2: вычисление углов треугольника

Углы треугольника могут быть найдены с использованием различных формул и методов, в зависимости от доступных данных. В данном случае предлагается использовать теорему косинусов.
Теорема косинусов устанавливает связь между длинами сторон треугольника и косинусами его углов. Формула теоремы косинусов имеет вид:
c^2 = a^2 + b^2 - 2ab*cos(C)
где а и b - длины сторон треугольника, а C - угол между этими сторонами.
Используя данную формулу для каждого из трех углов, можно вычислить значения этих углов. Для этого необходимо знать длины сторон треугольника, которые можно вычислить с помощью координат вершин, полученных на предыдущем шаге.
После вычисления углов треугольника, можно использовать эти значения для различных целей. Например, для определения, является ли треугольник остроугольным, тупоугольным или прямоугольным.
Таким образом, вычисление углов треугольника является важным этапом в работе с треугольниками и позволяет получить дополнительную информацию о их свойствах и форме.
Шаг 3: вычисление координат вершин треугольника
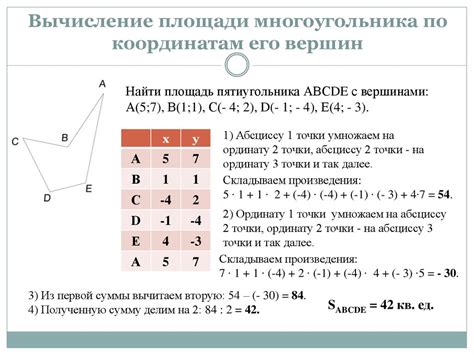
После определения длин и углов вектора, можно перейти к вычислению координат вершин треугольника.
Для этого используется преобразование координат вектора в соответствии с формулами в зависимости от позиции вектора:
1. Для первой вершины треугольника, координаты вычисляются с использованием следующих формул:
x1 = x0 + length * cos(angle1) y1 = y0 + length * sin(angle1)где x0 и y0 - начальные координаты вектора, length - длина вектора, angle1 - угол вектора.
2. Аналогичные вычисления проводятся для второй вершины треугольника:
x2 = x0 + length * cos(angle2) y2 = y0 + length * sin(angle2)3. Для третьей вершины треугольника, используется формула:
x3 = x0 + length * cos(angle3) y3 = y0 + length * sin(angle3)Таким образом, у нас есть полный алгоритм нахождения координат вершин треугольника по координатам вектора. Эти координаты могут быть использованы для дальнейших вычислений или отображения треугольника на экране.
Примеры нахождения вершин треугольника
В следующих примерах рассмотрим алгоритм нахождения вершин треугольника по координатам вектора.
Пример 1:
- Задан вектор AB с координатами A(x1, y1, z1) и B(x2, y2, z2).
- Находим длину каждой стороны треугольника AB, BC и AC с помощью формулы расстояния между двумя точками в трехмерном пространстве.
- Находим углы треугольника с помощью формулы косинуса.
- Находим координаты вершин треугольника путем решения системы уравнений, которая состоит из уравнения прямой AB и двух уравнений окружности с центром в точке A и радиусом равным длине стороны AC.
Пример 2:
- Задан вектор AD с координатами A(x1, y1, z1) и D(x3, y3, z3).
- Находим длину каждой стороны треугольника AD, BD и AB.
- Находим углы треугольника с помощью формулы косинуса.
- Находим координаты вершин треугольника путем решения системы уравнений, которая состоит из уравнения прямой AD и двух уравнений окружности с центром в точке A и радиусом, равным длине стороны AB.
Пример 3:
- Задан вектор AC с координатами A(x1, y1, z1) и C(x4, y4, z4).
- Находим длину каждой стороны треугольника AC, BC и AB.
- Находим углы треугольника с помощью формулы косинуса.
- Находим координаты вершин треугольника путем решения системы уравнений, которая состоит из уравнения прямой AC и двух уравнений окружности с центром в точке A и радиусом, равным длине стороны AB.
Таким образом, с помощью данных алгоритмов можно определить координаты вершин треугольника, используя координаты вектора.
Объяснения алгоритма нахождения вершин треугольника

Алгоритм нахождения вершин треугольника по координатам вектора основан на известных свойствах геометрии и применяется для определения положения точек треугольника в трехмерном пространстве.
Для начала, нужно знать координаты трех точек - вершин треугольника. Назовем эти точки A, B и C. Вектор AB представляется как (Bx - Ax, By - Ay, Bz - Az), где Ax, Ay, Az - координаты точки A, а Bx, By, Bz - координаты точки B. Аналогично, вектор AC представляется как (Cx - Ax, Cy - Ay, Cz - Az).
Следующий шаг - найти векторное произведение векторов AB и AC. Векторное произведение векторов AB и AC определяет нормаль к плоскости, на которой лежит треугольник. Нормализуем этот вектор, чтобы получить единичный вектор нормали плоскости.
Зная нормаль плоскости и координаты одной из вершин (например, A), можно найти уравнение плоскости, на которой лежит треугольник. Уравнение плоскости имеет вид Ax + By + Cz + D = 0, где A, B, C и D - коэффициенты, которые определяются вектором нормали и координатами точки A.
Наконец, чтобы найти координаты вершин треугольника, подставляем значения переменных x, y и z в уравнение плоскости. Координаты вершин треугольника получаются при решении системы уравнений.
Таким образом, алгоритм нахождения вершин треугольника по координатам вектора состоит из следующих шагов: нахождение вектора нормали плоскости, нахождение уравнения плоскости и подстановка значений переменных в уравнение для получения координат вершин треугольника.