В геометрии вписанная окружность – это окружность, которая касается всех сторон треугольника. Знание радиуса вписанной окружности может облегчить решение различных задач, связанных с треугольниками. В данной статье мы рассмотрим, как найти сторону треугольника по заданному радиусу вписанной окружности.
Для начала вспомним, что вписанная окружность треугольника делит каждую из сторон пополам. Также известно, что радиус вписанной окружности является высотой треугольника, опущенной из его вершины на сторону треугольника.
Обозначим стороны треугольника как a, b и c, а радиус вписанной окружности как r. По теореме Пифагора, очевидно, что (a/2)^2 + r^2 = a^2. Используя это уравнение, можно выразить сторону треугольника a через радиус вписанной окружности: a = 2r√3.
Как вычислить сторону треугольника
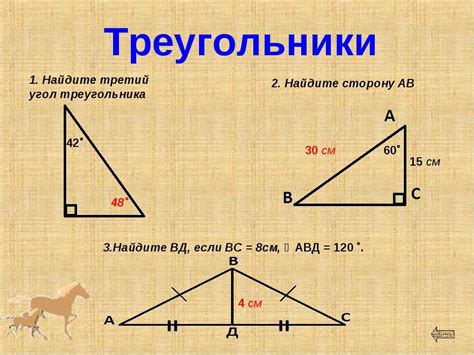
Вычисление стороны треугольника может быть полезным, когда известны другие стороны или углы, или когда треугольник представляет собой особую геометрическую фигуру, например, равносторонний треугольник.
Для вычисления стороны треугольника существует несколько методов. Один из них основан на использовании теоремы Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Если известны две стороны треугольника, можно воспользоваться теоремой косинусов. Она позволяет выразить одну сторону через две другие стороны и угол между ними.
Если известны все три стороны треугольника, можно воспользоваться формулой полупериметра, которая позволяет вычислить площадь треугольника и его стороны.
В случае равностороннего треугольника, все стороны имеют одинаковую длину. Для вычисления стороны такого треугольника достаточно знать длину одной из сторон.
Важно помнить, что для вычисления стороны треугольника необходимо иметь достаточно информации о треугольнике, такую как длины сторон или углы.
Методы вычисления стороны треугольника
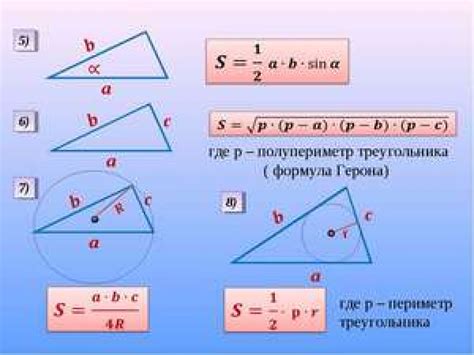
Существует несколько способов вычисления стороны треугольника, в зависимости от данных, которые известны.
Если известны длины двух сторон и угол между ними, можно воспользоваться теоремой косинусов. Эта теорема позволяет найти третью сторону треугольника по формуле:
| a^2 = b^2 + c^2 - 2bc * cos(A) |
Где a - искомая сторона, b и c - известные стороны, A - известный угол.
Если известны длины всех трех сторон треугольника, можно воспользоваться формулой площади треугольника Герона:
| S = sqrt(p * (p - a) * (p - b) * (p - c)) |
Где S - площадь треугольника, a, b и c - стороны треугольника, p - полупериметр (p = (a + b + c) / 2).
Если известны радиус вписанной окружности треугольника и длины двух сторон, можно воспользоваться формулой:
| r = sqrt(((p - a) * (p - b) * (p - c)) / p) |
Где r - радиус вписанной окружности, a, b и c - стороны треугольника, p - полупериметр (p = (a + b + c) / 2).
Это лишь некоторые методы вычисления стороны треугольника. Известно, что существуют и другие методы, решающие эту задачу для различных вариантов данных. Выбор метода зависит от известных данных и требуемой точности.
Радиус вписанной окружности и сторона треугольника
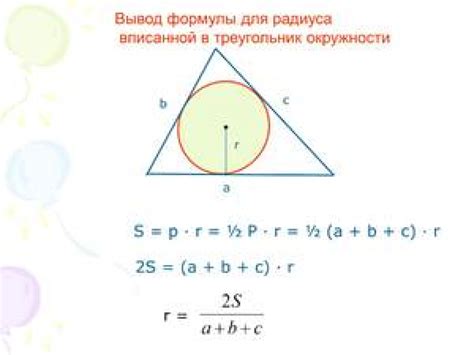
Для нахождения стороны треугольника по радиусу вписанной окружности можно воспользоваться формулой:
| Формула | Описание |
|---|---|
| a = 2r * tan(π/3) | Формула для равностороннего треугольника |
| a = 2r * sin(α) | Формула для треугольника с известным углом α |
| a = 2r * cos(β) | Формула для треугольника с известным углом β |
Где a - длина стороны треугольника, r - радиус вписанной окружности, α и β - углы треугольника.
Таким образом, зная радиус вписанной окружности и характеристики треугольника (равносторонний, с определенными углами), можно легко определить длину его стороны и использовать эту информацию в решении задач геометрии.