Алгоритм пересечения отрезков на плоскости — точный расчет пересечения двух отрезков, рассмотрение алгоритма с подробным руководством и программными примерами

Пересечение отрезков на плоскости – это важная задача в компьютерной графике, геометрии и алгоритмике. Она возникает во многих приложениях, начиная от построения трехмерных моделей и заканчивая обработкой изображений. Правильное определение пересечения отрезков позволяет эффективно решать такие задачи, как нахождение ближайших точек соприкосновения объектов, рассчет площадей пересечений, определение видимости и многое другое.

В данной статье мы рассмотрим алгоритм точного расчета пересечения между двумя отрезками на плоскости. Мы подробно разберем все необходимые шаги и условия, чтобы вы могли легко реализовать этот алгоритм в своих проектах и приложениях.

В основе алгоритма лежит использование понятия вектора и его свойств. Определяя пересечение отрезков как точку, мы проверяем условия, в которых прямые, содержащие отрезки, пересекаются. Также мы рассмотрим случаи, когда отрезки могут быть параллельны или совпадать, и предложим соответствующие методы обработки.

Точный расчет пересечения отрезков на плоскости

Алгоритм пересечения отрезков на плоскости позволяет определить точное местоположение точки пересечения двух отрезков. Этот алгоритм работает на основе геометрических принципов и не требует сложных вычислений.

Для точного расчета пересечения отрезков, необходимо выполнить следующие шаги:

1. Найти уравнения прямых, на которых лежат отрезки. Это можно сделать, зная координаты начальных и конечных точек каждого отрезка.
2. Решить систему уравнений, составленную из уравнений прямых. В результате получим координаты точки пересечения прямых.
3. Проверить, лежат ли найденные координаты точки пересечения внутри обоих отрезков. Для этого нужно убедиться, что координаты точки пересечения находятся внутри отрезков.

Если координаты точки пересечения находятся внутри обоих отрезков, то это означает, что отрезки пересекаются. Если координаты точки пересечения находятся вне одного из отрезков, то пересечение отрезков отсутствует.

Метод точного расчета пересечения отрезков является надежным и позволяет определить пересечение с высокой точностью. Однако он требует некоторой предварительной подготовки и выполнения нескольких шагов. Полученные результаты точного расчета могут быть использованы для различных целей, например, для определения пересечений линий на плоскости или для нахождения точек пересечения в графических приложениях.

Подробное руководство по алгоритму

Для выполнения этого алгоритма требуется следующая информация: координаты начала и конца каждого отрезка.

Шаги алгоритма:

1. Проверить, пересекаются ли отрезки хотя бы в одной точке. Для этого сравните координаты конца первого отрезка с координатами начала и конца второго отрезка, и наоборот.
2. Если отрезки пересекаются, то расчет точного пересечения. Для этого используйте формулы для нахождения координат точки пересечения прямых.
3. Проверьте, лежит ли найденная точка пересечения внутри обоих отрезков. Для этого проверьте, что координаты точки лежат между соответствующими координатами начала и конца отрезков.
4. Если точка пересечения лежит внутри обоих отрезков, то это точное пересечение отрезков. Если точка лежит на границе одного из отрезков, то это также считается пересечением.

Следующий пример иллюстрирует применение алгоритма пересечения отрезков на плоскости:

Point A: (1, 1)
Point B: (4, 4)
Point C: (2, 3)
Point D: (5, 2)
Step 1: Отрезки AB и CD пересекаются, так как точка C (2, 3) находится между точками A (1, 1) и B (4, 4), и точка D (5, 2) находится между точками A (1, 1) и B (4, 4).
Step 2: Вычисляем координаты точки пересечения. Используем формулы для нахождения координат точки пересечения прямых.
Step 3: Проверяем, лежит ли точка пересечения (3, 3) внутри обоих отрезков. Так как точка находится между точками A (1, 1) и B (4, 4) и точкой C (2, 3) и D (5, 2), то это точное пересечение отрезков.
Step 4: Результат - точное пересечение отрезков AB и CD в точке (3, 3).

Алгоритм пересечения отрезков на плоскости имеет широкий спектр применений, включая компьютерную графику, геометрические вычисления и специализированные алгоритмы для работы с графами. Знание и использование этого алгоритма является важной частью основ геометрии и компьютерной графики.

Примеры визуализации алгоритма пересечения отрезков

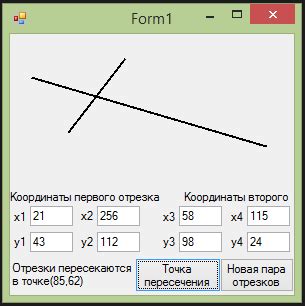
• Пример 1: На первом рисунке изображены два отрезка, AB и CD. С использованием алгоритма пересечения отрезков, видно, как точка E получается как точка пересечения отрезков AB и CD. Наглядность визуализации помогает понять, что алгоритм работает правильно и находит точное место пересечения.
• Пример 2: Во втором примере представлены пересекающиеся отрезки EF и GH. С использованием визуализации алгоритма можно увидеть, что точка I является точкой пересечения отрезков EF и GH. Визуализация помогает понять, как работает алгоритм при пересечении отрезков, скрещивающихся под углом.

Таким образом, визуализация алгоритма пересечения отрезков является полезным инструментом для понимания его работы. Визуальное представление позволяет увидеть, как точно алгоритм работает и как он находит точку пересечения отрезков на плоскости.