Поиск в ширину и поиск в глубину - два основных алгоритма, используемых в области компьютерных наук для поиска пути или решения задачи. Оба алгоритма широко применяются в различных областях, от поиска в интернете до решения логических головоломок.
Алгоритм поиска в ширину использует принцип "волновой распространения" для поиска. Он начинает с начальной точки и исследует все соседние точки на первом уровне, затем переходит ко второму уровню и так далее, пока не достигнет целевой точки или не исследует все доступные узлы. Этот алгоритм обеспечивает минимальную глубину поиска и гарантирует нахождение кратчайшего пути, если таковой существует.
Алгоритм поиска в глубину, напротив, использует принцип "проб и ошибок". Он начинает с начальной точки и двигается в глубину, посещая каждую соседнюю точку до тех пор, пока не достигнет конечной точки или не окажется в тупике. Затем алгоритм отступает на один шаг назад и продолжает поиски, выбирая следующую доступную точку. Поиск продолжается до тех пор, пока не будут исследованы все доступные варианты.
Главное отличие между поиском в ширину и поиском в глубину заключается в порядке исследования узлов. Поиск в ширину исследует сначала узлы на одном уровне, затем переходит на следующий уровень и так далее. С другой стороны, поиск в глубину исследует узлы по одному, двигаясь все глубже и глубже в структуру данных.
Оба алгоритма имеют свои преимущества и недостатки, и выбор между ними зависит от конкретной задачи или структуры данных. Поиск в ширину хорошо подходит для нахождения кратчайшего пути или графа, а поиск в глубину может быть полезен для обхода дерева или поиска всех возможных путей.
Определение алгоритмов поиска в ширину и глубину
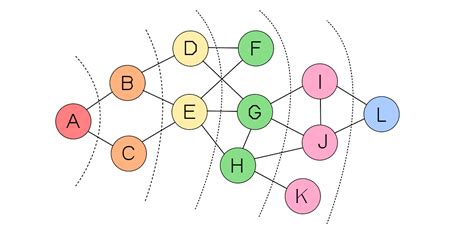
Алгоритм поиска в ширину (BFS) проходит через узлы графа или дерева по уровням, начиная с вершины или корня. На каждом уровне BFS обрабатывает все соседние вершины перед переходом к следующему уровню. Он использует структуру данных очередь для хранения вершин, которые нужно посетить.
Алгоритм поиска в глубину (DFS), напротив, проходит через граф или дерево сначала вглубь каждой ветки перед тем, как переходить к следующей. Он использует структуру данных стек для хранения узлов в порядке их обработки. DFS может быть реализован как рекурсивная функция или с помощью стека.
Основное отличие между алгоритмами BFS и DFS заключается в порядке обработки узлов. BFS гарантированно найдет кратчайший путь до целевой вершины, но потребует больше памяти для хранения информации о посещенных и ожидающих вершинах. DFS, в свою очередь, может потребовать меньше памяти, но не гарантирует нахождение кратчайшего пути, так как может зациклиться в графе с циклами.
Выбор между алгоритмами BFS и DFS зависит от конкретной задачи и требований. Оба алгоритма имеют свои преимущества и недостатки, и, в зависимости от ситуации, один из них может быть более эффективным или удобным.
Принцип работы алгоритма поиска в ширину
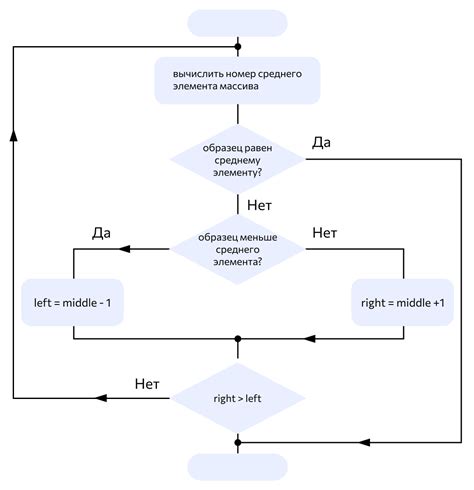
Алгоритм поиска в ширину используется для поиска кратчайшего пути от одной вершины графа до другой. Он основан на принципе обхода графа "в ширину", начиная с заданной вершины и постепенно расширяя область поиска находящимися на одном уровне вершинами.
Прежде всего, алгоритм помещает стартовую вершину в очередь. Затем он извлекает вершину из очереди и помечает ее как посещенную. Затем алгоритм проверяет все смежные вершины текущей вершины и помещает их в очередь, если они еще не были посещены. Таким образом, все вершины на одном уровне добавляются в очередь перед переходом к следующему уровню.
Алгоритм продолжает обходить граф до тех пор, пока не достигнет искомой вершины или пока очередь не опустеет. Если искомая вершина не найдена, значит, пути между заданными вершинами не существует.
В результате работы алгоритма поиска в ширину строится древовидная структура, называемая деревом поиска в ширину или графом кратчайших путей. Это дерево содержит путь с минимальным количеством шагов от начальной вершины до всех остальных вершин графа.
Принцип работы алгоритма поиска в глубину
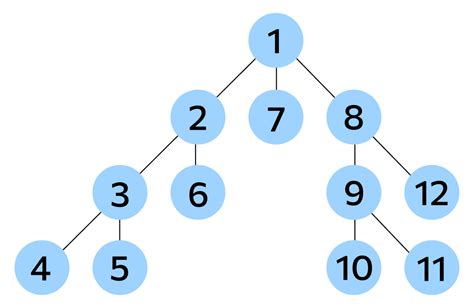
Принцип работы состоит в следующем:
- Выбирается стартовая вершина, с которой начинается обход.
- Посещение вершины - это процесс перехода из одной вершины в другую. После посещения вершины, она помечается как посещенная, чтобы избежать повторных посещений.
- Алгоритм перемещается к следующей непосещенной вершине, которая является соседом текущей вершины.
- Шаги 2 и 3 повторяются, пока не будут посещены все вершины графа или пока не будет достигнута конечная вершина.
- Если все вершины графа посещены, алгоритм завершается. В противном случае, если есть непосещенные вершины, алгоритм возвращает предыдущую вершину и продолжает поиск.
Алгоритм поиска в глубину имеет несколько преимуществ. Он прост в реализации и часто используется при работе с небольшими графами или задачами на поиск пути в лабиринте. Кроме того, он позволяет обходить все вершины графа и находить соответствующие решения.
Однако, алгоритм поиска в глубину может оказаться неэффективным при работе с большими графами или в случае, когда нужно найти оптимальное решение. В таких случаях, более эффективным может быть алгоритм поиска в ширину.
Особенности алгоритма поиска в ширину
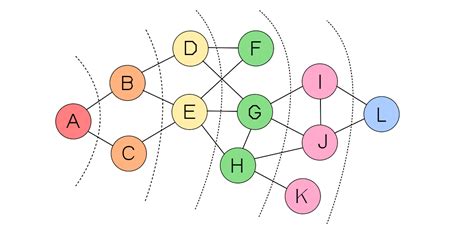
Одной из ключевых особенностей алгоритма BFS является использование очереди для хранения и обработки вершин графа. Изначально в очередь помещается стартовая вершина, а затем на каждом шаге исследования берется следующая вершина из очереди. После этого добавляются все смежные с ней вершины, которые еще не были исследованы. Таким образом, исследование происходит слоями: сначала обрабатываются все вершины первого слоя, затем второго и так далее, пока не будет достигнут конечный пункт или все вершины графа не будут исследованы.
Другой важной особенностью алгоритма BFS является его способность находить кратчайший путь от стартовой вершины до каждой другой вершины графа. Это происходит благодаря тому, что алгоритм исследует слои графа последовательно, а значит, находит ближайшие к стартовой вершине. Более того, BFS может быть использован для поиска всех путей между двумя вершинами графа, не только кратчайших.
| Преимущества алгоритма BFS | Недостатки алгоритма BFS |
|---|---|
|
|
Особенности алгоритма поиска в глубину

Определяющим фактором в алгоритме поиска в глубину является стек - структура данных, используемая для хранения вершин, которые еще не были полностью исследованы. Когда алгоритм достигает конца пути или не может больше продвигаться вперед, он возвращается в предыдущую вершину, чтобы исследовать другие возможные пути.
Преимущество алгоритма поиска в глубину заключается в том, что он позволяет нам исследовать все пути из начальной вершины, прежде чем переходить к следующей. Это особенно полезно в задачах, где мы хотим исследовать наличие или отсутствие пути между двумя вершинами, или найти все пути между ними.
Однако алгоритм поиска в глубину также имеет свои недостатки. В отличие от алгоритма поиска в ширину, он может попасть в бесконечный цикл, если граф содержит циклы. Кроме того, если граф имеет большую глубину, алгоритм может столкнуться с проблемами с памятью или занимать больше времени в сравнении с алгоритмом поиска в ширину.
Необходимо учесть, что алгоритм поиска в глубину не является универсальным решением для всех задач обхода графов. В некоторых случаях более подходящим может быть использование алгоритма поиска в ширину или другого алгоритма. Корректный выбор алгоритма обхода зависит от конкретной задачи и структуры графа, с которым мы работаем.
Примеры практического применения алгоритма поиска в ширину
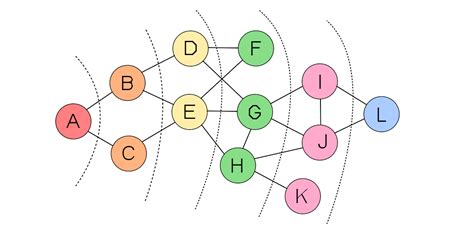
| Пример применения | Описание |
|---|---|
| Поиск пути в играх | Алгоритм поиска в ширину может быть использован для поиска оптимального пути в компьютерных играх. Например, при разработке игры с лабиринтом, алгоритм будет искать кратчайший путь от начальной точки до финиша, учитывая все преграды и возможности передвижения персонажа. Это позволяет создать более интересную и сложную игровую среду для игроков. |
| Обход дерева файловой системы | При работе с файловой системой, алгоритм поиска в ширину может быть использован для обхода дерева каталогов и файлов. Начиная с корневого каталога, он будет последовательно обходить все подкаталоги и файлы в каждом уровне иерархии. Это позволяет выполнить определенные операции для каждого элемента в файловой системе, такие как копирование, перемещение или удаление. |
| Поиск веб-страниц | Веб-краулеры, такие как поисковые системы и веб-скрейперы, могут использовать алгоритм поиска в ширину для обхода веб-страниц и сбора информации. Начиная с главной страницы, алгоритм будет последовательно переходить по всем ссылкам, найденным на каждой странице. Это позволяет собрать информацию с различных страниц и создать индексированную базу данных с обширным контентом. |
Все эти примеры демонстрируют практическое применение алгоритма поиска в ширину в различных областях. Благодаря своей эффективности и простоте, алгоритм поиска в ширину является важным инструментом для решения различных задач, связанных с обходом и поиском в графах и других структурах данных.
Примеры практического применения алгоритма поиска в глубину
Алгоритм поиска в глубину (Depth-First Search, DFS) широко используется в различных областях, включая информатику, графовые структуры и искусственный интеллект. Вот несколько примеров, где применение этого алгоритма доказало свою эффективность:
| Пример | Практическое применение |
|---|---|
| 1 | Определение связности графа |
| 2 | Поиск пути в лабиринте |
| 3 | Генерация музыкальных композиций |
| 4 | Поиск наиболее оптимального маршрута |
| 5 | Анализ и оценка возможных ходов в шахматах |
Алгоритм поиска в глубину основан на принципе постепенного исследования всех возможных путей в графе. Он позволяет находить определенные паттерны, оптимальные пути и выполнять анализ сложных структур данных. Это делает его полезным инструментом при решении широкого спектра задач.
Отличия между алгоритмами поиска в ширину и глубину
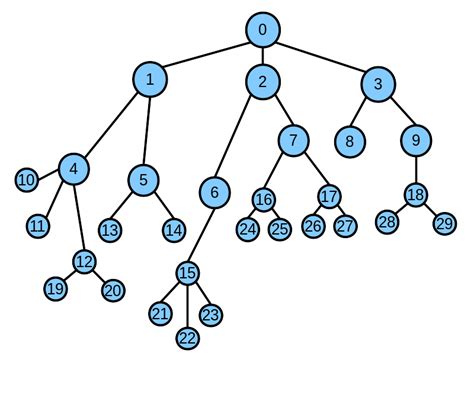
| Алгоритм поиска в ширину | Алгоритм поиска в глубину |
|---|---|
| В обходе графа поиск происходит на всех уровнях по очереди | В обходе графа поиск происходит по одному уровню до его полного исследования |
| Использует структуру данных "очередь" | Использует структуру данных "стек" |
| Для поиска кратчайшего пути между двумя вершинами | Не гарантирует поиск кратчайшего пути, но может использоваться для проверки наличия пути между вершинами |
| Обычно требует большего объема памяти | Обычно требует меньшего объема памяти |
Эти отличия между алгоритмами поиска в ширину и глубину определяют их применение и эффективность в различных задачах. Например, алгоритм поиска в ширину часто используется для нахождения кратчайшего пути в невзвешенном графе, а алгоритм поиска в глубину может быть полезен при проверке связности графа или нахождении циклов.