Бинарный поиск – это один из основных алгоритмов поиска, который позволяет находить элемент в упорядоченном списке. В отличие от простого поиска, бинарный поиск работает гораздо быстрее, особенно когда количество элементов в списке велико. Этот алгоритм находится в основе множества других алгоритмов и используется для решения различных задач.
Основная идея бинарного поиска заключается в том, что мы сокращаем рабочий диапазон поиска в два раза на каждой итерации. Для этого вычисляем средний элемент в текущем диапазоне и сравниваем его со значением, которое мы ищем. Если средний элемент равен искомому значению, поиск успешен. Если средний элемент меньше искомого, то мы можем исключить из рассмотрения все элементы, которые меньше или равны среднему. Если средний элемент больше искомого, то мы можем исключить из рассмотрения все элементы, которые больше или равны среднему.
Преимущество бинарного поиска заключается в его эффективности. При применении в упорядоченных списках с большим количеством элементов, бинарный поиск может значительно сократить время поиска. Например, при поиске элемента в списке из 100 элементов, простой поиск может потребовать в среднем 50 проверок, тогда как бинарный поиск всегда будет выполнять не более 7 проверок. Это делает бинарный поиск особенно полезным при работе с большими объемами данных.
Однако, для использования бинарного поиска необходимо, чтобы список был упорядочен. Если список неупорядочен, то перед применением бинарного поиска необходимо выполнить сортировку элементов списка. Также, алгоритм бинарного поиска не применим к динамическим или не отсортированным спискам, так как при вставке или удалении элементов необходимо перестраивать индексы элементов.
Определение и принцип работы
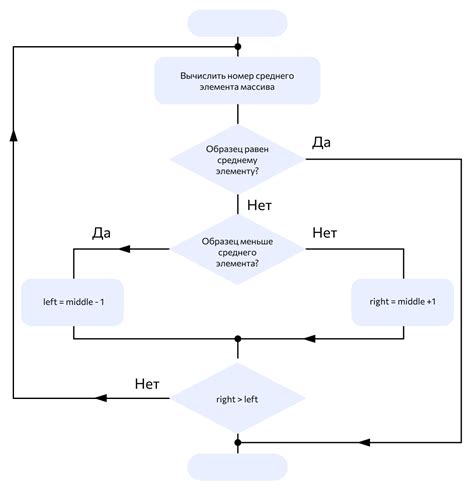
Принцип работы бинарного поиска заключается в следующих шагах:
- Устанавливается начальный и конечный индекс массива, обозначающие границы поиска.
- Находится средний индекс массива, путем вычисления суммы начального и конечного индексов, деленной на 2. Если сумма нечетная, то берется целая часть от деления.
- Значение среднего элемента сравнивается с искомым значением. Если средний элемент равен искомому значению, то поиск считается успешным и возвращается индекс этого элемента.
- Если искомое значение меньше среднего элемента, то конечный индекс сдвигается на значение среднего индекса минус 1, иначе начальный индекс сдвигается на значение среднего индекса плюс 1.
- Шаги 2-4 повторяются до тех пор, пока не будет найдено искомое значение или границы поиска сойдутся, что означает, что искомого значения в массиве нет.
Бинарный поиск является одним из самых эффективных и быстрых алгоритмов поиска, особенно при работе с большими объемами данных.
Применение бинарного поиска
Бинарный поиск наиболее эффективен в ситуациях, когда данные расположены в отсортированном порядке. Он может быть использован для поиска элементов в упорядоченных массивах, списках или базах данных. Благодаря своей эффективности, бинарный поиск является предпочтительным методом поиска в больших данных.
Одним из основных преимуществ бинарного поиска является его скорость работы. При каждой итерации поиска диапазон выборки уменьшается вдвое, что позволяет быстро находить искомый элемент в отсортированных данных. В сравнении с линейным поиском, который проверяет каждый элемент по одному, бинарный поиск может значительно уменьшить количество операций, особенно при больших объемах данных.
Бинарный поиск также применяется в алгоритмах сортировки, таких как быстрая, слиянием и пирамидальная сортировки. Он используется для разбиения данных на части и последующего сортировочного процесса. Это позволяет эффективно сортировать большие массивы или списки.
Однако следует учитывать, что бинарный поиск требует предварительной сортировки данных. Если данные не отсортированы, то необходимо вначале выполнить сортировку, что может занять дополнительное время. Кроме того, бинарный поиск может быть затруднен в случаях, когда в данных присутствуют повторяющиеся элементы или необходимо находить наименьший или наибольший элемент.
Эффективность бинарного поиска

Бинарный поиск обеспечивает временную сложность O(log n), где n - количество элементов в массиве. Это значит, что время выполнения алгоритма увеличивается логарифмически с увеличением размера массива. В сравнении с линейным поиском, который имеет временную сложность O(n), бинарный поиск значительно быстрее при работе с большими наборами данных.
Однако, бинарный поиск применим только к упорядоченным массивам. Это ограничение существенно, но при правильной организации данных оно невелико. Кроме того, бинарный поиск необходимо проводить на отсортированном массиве, что может потребовать некоторой предварительной подготовки данных.
Применение бинарного поиска может привести к значительному повышению эффективности работы программ, особенно при работе с большими объемами данных. Бинарный поиск является одним из наиболее эффективных алгоритмов поиска в отсортированных массивах и отлично справляется со своей задачей.
Особенности использования
Одной из главных особенностей использования бинарного поиска является необходимость предварительной сортировки массива. Бинарный поиск работает только с отсортированными данными, поэтому перед его применением нужно убедиться в правильной упорядоченности элементов.
Кроме того, бинарный поиск предполагает постоянный доступ к элементам массива. Так как алгоритм опирается на тот факт, что элементы массива расположены в отсортированном порядке, он должен иметь возможность быстро получать доступ к любому элементу по его индексу.
Еще одной важной особенностью использования бинарного поиска является возможность работы только с одномерными массивами. Алгоритм не может быть применен к многомерным структурам данных, так как он требует постоянного доступа к элементам массива по индексу.