Решение уравнений с двумя неизвестными является одной из ключевых задач в математике. Оно имеет широкое применение в различных сферах, начиная от физики и экономики, и заканчивая инженерией и компьютерной графикой. Но как можно эффективно решать подобные уравнения? В данной статье мы рассмотрим несколько методов и приемов, которые помогут нам справиться с этой задачей быстро и точно.
Один из самых простых и известных методов решения уравнений с двумя неизвестными - подстановка. Этот метод основан на замене неизвестных в уравнении на другие переменные и последующем нахождении их значений. Например, если у нас есть уравнение вида x + y = 10 и x - y = 2, мы можем заменить одну из переменных на другую и получить одну переменную уравнение, которое легко решить.
Еще одним эффективным методом решения уравнений с двумя неизвестными является метод определителей. Этот метод основан на определении матрицы, составленной из коэффициентов перед неизвестными в уравнении. Затем мы находим определитель этой матрицы и сравниваем его с нулем. Если определитель равен нулю, то уравнение имеет бесконечное количество решений, если нет, то уравнение имеет единственное решение.
Ключевые особенности уравнений с двумя неизвестными
Одной из ключевых особенностей уравнений с двумя неизвестными является то, что они представляют собой системы уравнений. В системе уравнений каждое уравнение содержит две неизвестные величины, и решение системы состоит в нахождении значений этих неизвестных, при которых все уравнения системы выполняются одновременно.
Второй особенностью уравнений с двумя неизвестными является то, что для их решения требуется минимум два независимых уравнения. Если имеется только одно уравнение, то оно может иметь множество решений, так как значения одной неизвестной можно свободно выбирать, и величина второй неизвестной будет определяться этим единственным уравнением.
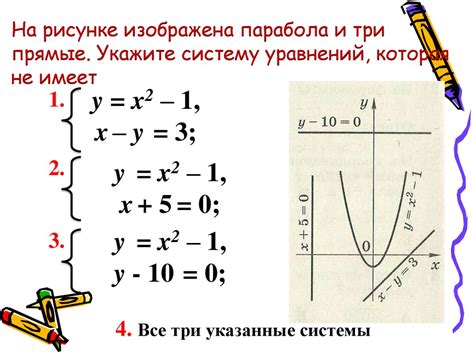
Третья особенность уравнений с двумя неизвестными связана с их геометрическим представлением. Можно представить систему уравнений в пространстве двух неизвестных координат, и решение системы будет соответствовать точке или множеству точек на плоскости. Таким образом, решение системы уравнений с двумя неизвестными может быть представлено в виде геометрической фигуры, например, прямой, окружности, параболы и т.д.
Изучение уравнений с двумя неизвестными позволяет не только развивать математическое мышление и логику, но и находить практическое применение. Такие уравнения широко используются в физике, экономике, статистике, анализе данных и других науках, где необходимо моделирование и решение задач, связанных с двумя переменными величинами.
Основные методы решения скалярных уравнений

Метод подстановки:
Данный метод заключается в подстановке значения одной из переменных в уравнение и последующем решении полученного уравнения относительно другой переменной. Затем найденное значение подставляется обратно в исходное уравнение, чтобы найти значение первой переменной.
Метод равных коэффициентов:
Этот метод применяется, когда оба уравнения имеют одинаковые коэффициенты при одной и той же переменной. В таком случае можно выразить одну переменную через другую и подставить это выражение во второе уравнение. Затем полученное уравнение решается относительно одной переменной.
Метод графического представления:
В этом методе уравнения с двумя неизвестными представляются графически на координатной плоскости. Решением системы уравнений будет точка пересечения графиков. Если графики не пересекаются, то система уравнений не имеет решений. Если графики параллельны, то система уравнений имеет бесконечное множество решений.
Метод исключения:
Этот метод основан на последовательном исключении одной переменной из системы уравнений. Для этого уравнения со сложными коэффициентами приводят к уравнениям с одинаковыми коэффициентами и затем уравнения вычитают, чтобы получить новое уравнение с одной переменной. Затем эта переменная подставляется в одно из исходных уравнений, чтобы найти значение другой переменной.
Метод подстановки:
Данный метод заключается в подстановке значения одной из переменных в уравнение и последующем решении полученного уравнения относительно другой переменной. Затем найденное значение подставляется обратно в исходное уравнение, чтобы найти значение первой переменной.
Метод равных коэффициентов:
Этот метод применяется, когда оба уравнения имеют одинаковые коэффициенты при одной и той же переменной. В таком случае можно выразить одну переменную через другую и подставить это выражение во второе уравнение. Затем полученное уравнение решается относительно одной переменной.
Метод графического представления:
В этом методе уравнения с двумя неизвестными представляются графически на координатной плоскости. Решением системы уравнений будет точка пересечения графиков. Если графики не пересекаются, то система уравнений не имеет решений. Если графики параллельны, то система уравнений имеет бесконечное множество решений.
Метод исключения:
Этот метод основан на последовательном исключении одной переменной из системы уравнений. Для этого уравнения со сложными коэффициентами приводят к уравнениям с одинаковыми коэффициентами и затем уравнения вычитают, чтобы получить новое уравнение с одной переменной. Затем эта переменная подставляется в одно из исходных уравнений, чтобы найти значение другой переменной.
Эффективные приемы решения систем уравнений

Решение систем уравнений с двумя неизвестными может быть сложной задачей, однако существуют несколько эффективных приемов, которые позволяют быстро и точно найти решение.
Первым приемом является метод подстановки. Он заключается в том, что мы выражаем одну из переменных через другую из одного уравнения, а затем подставляем это выражение во второе уравнение. После этого мы получаем уравнение с одной переменной, которое можно решить с помощью привычных способов.
Другим эффективным приемом является метод сложения или вычитания уравнений. Для этого мы складываем или вычитаем изначальные уравнения так, чтобы одна из переменных исчезла. После этого полученное уравнение решаем и находим значение одной переменной. Затем это значение подставляем в одно из исходных уравнений и находим вторую переменную.
Третьим приемом является метод определителей. Он основан на матричном представлении системы уравнений. Мы записываем коэффициенты при переменных в матрицу и находим ее определитель. Если определитель не равен нулю, то система уравнений имеет единственное решение. Затем мы используем обратные матрицы и умножение для нахождения значений переменных.
Независимо от выбранного приема, важно правильно представить систему уравнений и точно применять выбранный метод. Также необходимо проверять решение, подставляя найденные значения переменных в исходные уравнения и убеждаясь, что они удовлетворяют системе в целом. Эффективность приемов решения систем уравнений возрастает с практикой, поэтому рекомендуется регулярно тренироваться на разных примерах.
Практическое применение методов решения уравнений

Финансы: Решение уравнений с двумя неизвестными может быть полезно при расчете финансовых показателей. Например, при определении стоимости товаров или услуг, их объема или цены.
Физика: В физике могут возникать ситуации, в которых нужно решить уравнения с двумя неизвестными для определения различных параметров, таких как скорость, ускорение или сила. Это может быть полезно при решении задач на кинематику или динамику.
Инженерия: При проектировании и строительстве инженеры часто сталкиваются с необходимостью решать уравнения с двумя неизвестными для определения размеров, пропорций и других параметров объектов.
Экономика: Методы решения уравнений применяются в экономическом анализе, чтобы оценить взаимосвязь между различными переменными и прогнозировать результаты будущих событий.
Компьютерные науки: При программировании и алгоритмических задачах может возникнуть необходимость решить уравнения для определения значений переменных, контроля потока выполнения или оптимизации времени и ресурсов.
В жизни каждого человека есть множество ситуаций, где методы решения уравнений с двумя неизвестными могут быть применены для решения проблем и принятия обоснованных решений. Это может быть умение оценить финансовые показатели, прогнозировать тенденции развития, решать технические или научные задачи и т.д. Овладение этими методами поможет развить аналитическое мышление и навыки принятия решений, которые могут быть полезными в различных областях жизни и работы.