Центр круга - это геометрическая точка, которая находится на равном удалении от всех точек круга. Найти эту точку может быть очень полезно во многих сферах, в том числе в компьютерном зрении, компьютерной графике и робототехнике. Однако задача поиска центра круга не всегда тривиальна и требует применения специализированных методов и алгоритмов.
В данной статье рассмотрим несколько распространенных методов и алгоритмов, которые позволяют найти центр круга.
Первый метод основан на использовании геометрических свойств круга. Для этого необходимо иметь круг, заданный набором точек, которые лежат на его окружности. Используя геометрические формулы и свойства окружности, можно найти точку пересечения всех перпендикуляров, проведенных к сторонам круга. Эта точка будет являться центром круга.
Другой распространенный способ - метод наименьших квадратов. Он заключается в поиске такой точки, чтобы сумма квадратов расстояний от этой точки до всех заданных точек круга была наименьшей. В данном случае можно воспользоваться алгоритмом, который итеративно изменяет положение точки и вычисляет сумму квадратов расстояний, пока не будет достигнуто наименьшее значение.
Методы нахождения центра круга
Метод пересечения перпендикуляров. Данный метод основан на принципе, что перпендикуляры, проведенные к серединам отрезков с одной стороны, пересекаются в центре круга. Для определения центра круга по этому методу необходимо провести две перпендикулярные линии через четыре точки, лежащие на окружности. Их пересечение будет являться центром круга.
Метод минимизации расстояний. Этот метод основан на идее, что центр круга является точкой, минимизирующей сумму расстояний от всех точек на окружности до этой точки. Алгоритм нахождения центра по этому методу заключается в итеративном переборе различных возможных центров с последующим подсчетом суммарных расстояний до всех точек. Центр, при котором сумма расстояний минимальна, считается центром круга.
Метод наименьших квадратов. Этот метод основан на аппроксимации окружности набором точек с помощью метода наименьших квадратов. Алгоритм заключается в поиске окружности, которая наилучшим образом соответствует набору точек на плоскости. Центр такой окружности считается центром круга.
Метод анализа градиента. Данный метод основан на анализе градиента яркости изображения в окрестности окружности. Алгоритм заключается в поиске локального максимума градиента яркости, который соответствует центру круга. Для этого используются различные методы выделения границ и фильтрации изображения.
Выбор метода нахождения центра круга зависит от конкретной задачи и предпочтений разработчика. В некоторых случаях может быть эффективным комбинирование нескольких методов для достижения наилучших результатов.
Поиск центра круга по трем точкам
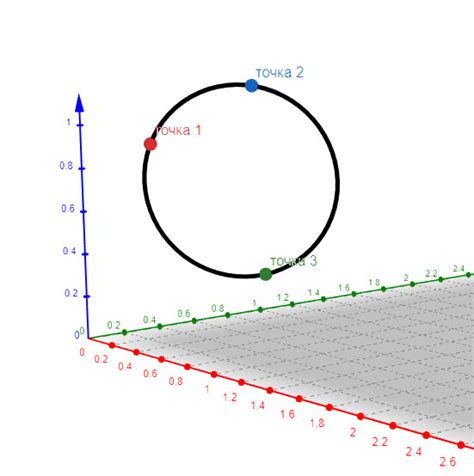
Существует несколько методов и алгоритмов для решения этой задачи, включая:
1. Метод перпендикуляров
В этом методе мы строим перпендикуляры к сторонам треугольника, проходящие через их середины. Центр круга будет пересечением этих перпендикуляров.
2. Метод окружностей
В этом методе мы строим окружности, проходящие через две из трех заданных точек. Центр круга будет пересечением этих окружностей.
3. Метод касательных
В этом методе мы строим касательные к сторонам треугольника, проходящие через третью заданную точку. Центр круга будет точкой пересечения этих касательных.
Все эти методы имеют свои преимущества и недостатки, и выбор метода зависит от конкретной ситуации. Они также могут использоваться для решения других задач, связанных с кругами, таких как поиск радиуса или проверка, принадлежит ли точка кругу.
Метод наименьших квадратов

Для применения метода наименьших квадратов необходимо иметь набор точек, для которых известны координаты. Эти точки могут быть получены из различных источников, таких как оптические системы, радары или GPS-навигация.
Алгоритм метода наименьших квадратов состоит из следующих шагов:
| Шаг | Описание |
| 1 | Задать начальное значение для координат центра круга |
| 2 | Вычислить расстояние от каждой точки до предполагаемого центра круга |
| 3 | Вычислить сумму квадратов всех расстояний |
| 4 | На основе полученной суммы определить новые координаты центра круга |
| 5 | Повторять шаги 2-4, пока сумма квадратов расстояний не станет минимальной |
После выполнения всех шагов алгоритма получаем координаты центра круга, описывающего заданный набор точек. Эти координаты можно использовать для различных целей, например, для определения положения объекта в пространстве или для корректировки пути движения.
Метод наименьших квадратов имеет свои преимущества и недостатки. Он достаточно прост в реализации и может быть применен в различных областях, связанных с анализом данных. Однако, для его работы необходимо иметь достаточное количество точек и учитывать возможные ошибки измерений.
Таким образом, метод наименьших квадратов является эффективным инструментом для поиска центра круга и может быть использован во множестве приложений.
Алгоритм нахождения центра круга по радиусам и диаметрам

- Создаем пустой массив для хранения всех возможных центров круга.
- Для каждого известного радиуса и диаметра:
- Вычисляем координаты возможного центра круга с помощью известного диаметра.
- Добавляем найденный центр круга в массив.
Данный алгоритм позволяет найти центр круга на плоскости, основываясь на известных радиусах и диаметрах. Он может быть полезен в различных областях, таких как компьютерное зрение, геометрическое моделирование и компьютерная графика. Для реализации алгоритма возможно использование любого языка программирования, подходящего для работы с числами и массивами.
Метод Екатерини

Для применения метода Екатерини необходимо провести две хорды, пересекающиеся под прямым углом на окружности. Затем определяется точка пересечения хорд, которая является центром круга.
Преимуществом этого метода является его простота и надежность. Он позволяет определить центр круга с высокой точностью, при условии правильного проведения хорд.
| Преимущества | Недостатки |
|---|---|
| Простота применения | Требуется проводить хорды под прямым углом |
| Высокая точность | Необходимость наличия окружности |
| Надежность | Не применим к неполным или овальным окружностям |
Таким образом, метод Екатерини является одним из важных инструментов при поиске центра круга. Он применим во многих областях, включая геометрию, физику, а также в компьютерном зрении и обработке изображений.
Алгоритм нахождения центра круга по пересечению окружностей
Для нахождения центра круга по пересечению окружностей существует специальный алгоритм, который позволяет определить координаты центра круга точно и эффективно. Этот алгоритм широко применяется в различных областях, связанных с геометрией и компьютерной графикой.
Первым шагом алгоритма является определение координат центров двух окружностей, пересекающихся. Для этого необходимо знать координаты центров и радиусы этих окружностей. После нахождения координат центров, происходит определение их расстояния. Это осуществляется с использованием формулы для вычисления расстояния между двумя точками в декартовой системе координат.
Затем следует уточнение координат центра круга методом интерполяции. Это позволяет определить точное положение центра круга на плоскости. Для этого используется формула интерполяции, которая учитывает отношение радиусов и расстояние между центрами окружностей. Интерполяция позволяет получить точные координаты центра круга в результате их вычисления.
В завершение алгоритма осуществляется проверка правильности найденного центра круга. Это делается путем вычисления расстояния от центра круга до пересечения окружностей. Если это расстояние равно радиусу окружности, то считаем алгоритм выполненным успешно и центр круга найден правильно.
Алгоритм нахождения центра круга по пересечению окружностей является эффективным и точным способом определения координат центра круга. Он находит широкое применение в различных областях, таких как геометрия, компьютерная графика, а также в задачах, связанных с определением положения объектов на плоскости.
Метод Маркельченко
Алгоритм работы метода Маркельченко заключается в следующих шагах:
- Выбор произвольной точки на окружности и обозначение ее как центр.
- Измерение расстояния от центра до каждой из остальных точек на окружности.
- Нахождение точки, расстояние от которой до центра наибольшее.
- Проведение прямой, проходящей через выбранную точку и центр.
- Нахождение середины отрезка, образованного пересечением прямой с окружностью.
- Продолжение процесса с найденной серединой в качестве нового центра и остальными точками на окружности.
Таким образом, метод Маркельченко позволяет последовательно находить центры окружностей с наибольшим радиусом, основываясь на измеренном расстоянии между точками. Этот метод широко применяется в геометрии и компьютерном зрении для решения задач, связанных с поиском и анализом форм и объектов.
| Точка | x | y |
|---|---|---|
| 1 | 3 | 6 |
| 2 | 7 | 2 |
| 3 | 1 | 9 |
| 4 | 4 | 4 |
Алгоритм поиска центра круга по ломаному контуру
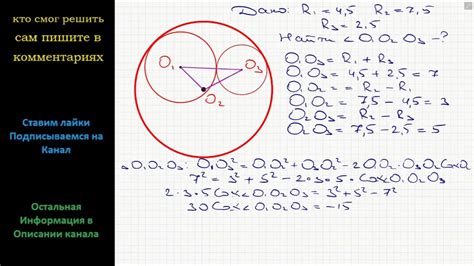
Алгоритм поиска центра круга по ломаному контуру основывается на анализе расстояний между точками контура и предположении, что центр круга будет лежать на линии, проходящей через среднюю точку самого удаленного сегмента контура.
Шаги алгоритма:
- Находим самый дальний сегмент контура. Вычисляем сумму длин всех сегментов ломаной.
- Для каждого сегмента находим его середину.
- Для каждой середины сегмента вычисляем расстояние до самой удаленной точки контура.
- Выбираем середину сегмента, у которой расстояние до самой удаленной точки минимально.
- Полученная середина является приближенным центром круга.
Алгоритм основывается на простой идее, что центр круга будет находиться рядом с серединой самого удаленного сегмента контура. Путем вычисления расстояний между точками контура и их серединой, мы можем определить, какая из середин находится ближе к самой удаленной точке. Это дает нам приблизительный центр круга, который может быть дальше точного центра, но все же близко к нему.