Параллелограмм – это особый вид четырехугольника, у которого противоположные стороны параллельны и равны между собой. Такая геометрическая фигура обладает несколькими уникальными свойствами, которые делают его интересным объектом изучения в математике.
Первое свойство параллелограмма – равенство противоположных сторон. Это означает, что любые две противоположные стороны параллелограмма имеют одинаковую длину. Однако, длины противоположных сторон могут быть различными, что делает параллелограмм максимально гибким в плане формы.
Второе свойство параллелограмма – параллельность противоположных сторон. Это означает, что любые две противоположные стороны параллелограмма всегда расположены параллельно друг другу. Это важное свойство позволяет использовать параллелограммы в различных областях, например, в архитектуре и инженерии.
Третье свойство параллелограмма – равенство противоположных углов. Это означает, что углы, образованные противоположными сторонами параллелограмма, имеют одинаковую величину. Это свойство обеспечивает симметрию и гармоничность параллелограмма, делая его эстетически привлекательным.
В целом, параллелограмм представляет собой геометрическую фигуру с уникальными свойствами, которые делают его полезным и интересным для изучения в математике и других науках. Этот четырехугольник имеет не только геометрическую важность, но также может встречаться в различных естественных и искусственных объектах, делая его актуальным и в повседневной жизни.
Что такое параллелограмм и его основные свойства
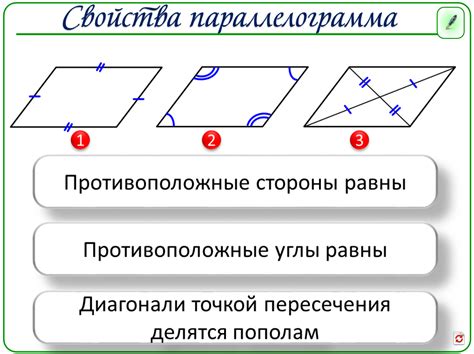
Основные свойства параллелограмма:
1. Противоположные стороны параллельны. Это означает, что если две стороны параллельны, то остальные две стороны также будут параллельны.
2. Противоположные стороны равны по длине. Это означает, что если две стороны параллельны и равны, то остальные две стороны также будут равны.
3. Углы при основании параллелограмма равны между собой. Это означает, что противоположные углы при основании параллелограмма равны.
4. Сумма углов параллелограмма равна 360 градусов. Это означает, что если сложить все углы параллелограмма, получится 360 градусов.
5. Диагонали параллелограмма делятся пополам. Это означает, что диагонали параллелограмма делят его на два равных треугольника.
6. Площадь параллелограмма равна произведению длины его основания на высоту, опущенную на это основание. Это означает, что для вычисления площади параллелограмма нужно умножить длину одной из его сторон на высоту, которая проведена из противоположного угла к этой стороне.
Определение параллелограмма и его геометрическая форма
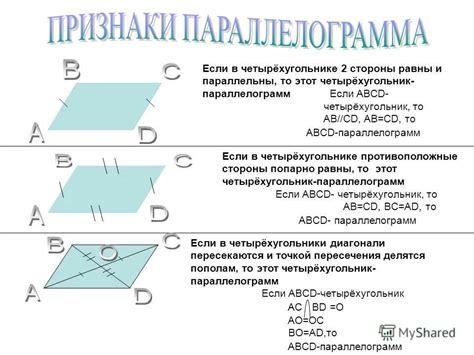
Геометрическая форма параллелограмма напоминает прямоугольник или ромб, но отличается от них тем, что его противоположные стороны не обязательно перпендикулярны. Все четыре стороны параллелограмма равны по длине и параллельны попарно. Это означает, что если взять две стороны параллелограмма и провести их в параллельных направлениях, они не пересекутся.
Форма параллелограмма может меняться, но его основные свойства остаются неизменными. Например, если одна сторона параллелограмма увеличивается или уменьшается, остальные три стороны соответственно изменяются, чтобы сохранить равенство. Это свойство называется параллельной трансляцией.
Также параллелограмм имеет свойство диагоналей: они делят его на две равные части, их точки пересечения (точка пересечения диагоналей) делят каждую диагональ пополам.
Различные формы параллелограмма могут иметь такие свойства, как симметрия и перпендикулярность диагоналей, но общие характеристики параллелограмма являются основой для определения и его геометрической формы и свойств.
Свойства параллелограмма и его основные характеристики
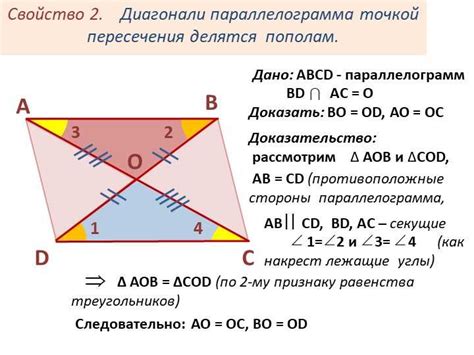
1. Углы: в параллелограмме противоположные углы равны между собой. То есть, если один угол параллелограмма равен α, то противоположный угол также равен α. Все углы внутри параллелограмма в сумме равны 360 градусов.
2. Стороны: противоположные стороны параллелограмма равны и параллельны. Обозначим их как AB и CD, BC и AD. Тогда AB = CD и BC = AD.
3. Диагонали: в параллелограмме диагонали делятся пополам. Если обозначить их как AC и BD, то точка пересечения диагоналей будет находиться в середине каждой из них, и AC = BD.
4. Площадь: площадь параллелограмма можно найти, умножив длину одной из сторон на высоту, опущенную на эту сторону. Формула для вычисления площади S: S = a * h, где a - длина основания, а h - высота.
5. Высота: в параллелограмме высота равна расстоянию между параллельными сторонами. Высота обозначается как h.
6. Периметр: периметр параллелограмма вычисляется по формуле: P = 2a + 2b, где a и b - длины сторон параллелограмма.
7. Площадь через диагонали: также площадь параллелограмма можно найти, зная длины его диагоналей. Формула для вычисления площади S: S = (AC * BD * sinα)/2, где sinα - синус угла между диагоналями.
Таким образом, зная любую из указанных характеристик, можно вычислить остальные свойства и параметры параллелограмма. Уникальные свойства параллелограмма делают его полезным в различных математических и геометрических задачах.
Примеры и применение параллелограмма в реальной жизни
Одним из наиболее очевидных примеров применения параллелограмма является строительство. В строительстве параллелограммы используются для создания прямоугольных структур, таких как стены и полы. Они помогают обеспечить прочность и стабильность конструкции, а также упрощают процесс измерения и выравнивания.
Параллелограммы также широко используются в графическом дизайне и искусстве. Они могут быть использованы для создания углов и перспективных отображений, а также для создания гармоничных композиций. Благодаря своим прямым углам и параллельным сторонам, параллелограммы могут помочь в создании симметрии и баланса в дизайне.
Параллелограммы также играют важную роль в механике и физике. Они могут быть использованы для моделирования движения твердых тел, включая вращение и трансляцию. Параллелограммы также могут быть использованы для расчета сил и моментов, обеспечивая понимание и предсказуемость физических процессов.
Кроме того, параллелограммы находят применение в повседневной жизни. Например, несколько параллелограммов могут быть использованы для создания сложной системы путей и дорожек в парках или на стадионах. Такая система может обеспечить безопасное движение людей и транспортных средств.
В целом, параллелограммы имеют широкий спектр применений в различных областях человеческой деятельности. Их форма и свойства делают их полезными инструментами для создания прочных и эстетически приятных структур, а также для моделирования и понимания физических процессов.