Синусоида - одна из самых известных и широко используемых функций в математике. Она представляет собой периодическую кривую, подобную волне, которая повторяется бесконечное количество раз. Мы можем наблюдать синусоиду во многих физических явлениях, например, в колебаниях звука, света или электричества.
Если дан график синусоиды, иногда необходимо восстановить функцию, которая его создала. Это может быть полезно во многих областях, включая физику, инженерию, статистику и музыку. В этом подробном руководстве мы рассмотрим, как построить функцию синусоиды по заданному графику.
Первым шагом является определение амплитуды и периода синусоиды. Амплитуда представляет собой максимальное значение функции, а период - расстояние между двумя последовательными повторениями синусоиды. Затем мы должны определить, где на графике начинается цикл повторений и в каком направлении идет синусоида: вверх или вниз.
Наше руководство поможет вам разобраться с построением функции синусоиды по графику и открыть для себя новые методы анализа и понимания этой важной математической функции.
Построение функции синусоиды
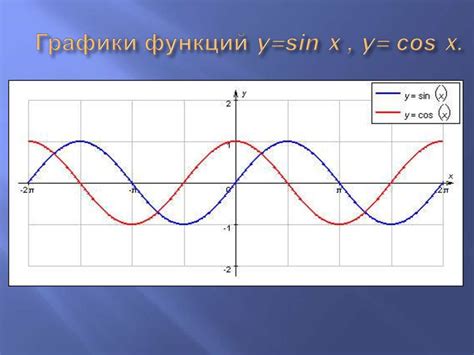
y = A * sin(B * x + C) + D
где:
- A – амплитуда (высота от пика до оси абсцисс);
- B – период (расстояние между двумя пиками);
- C – смещение по горизонтали (сдвиг влево или вправо);
- D – смещение по вертикали (сдвиг вверх или вниз).
Для построения графика функции синусоиды необходимо:
- Задать значения амплитуды, периода, смещения по горизонтали и по вертикали.
- Построить оси координат.
- Расчитать значение функции для заданных значений х.
- Отметить полученные точки на графике.
- Соединить полученные точки гладкой линией.
Важно помнить, что значение переменной x может быть представлено в радианах или градусах, в зависимости от выбранной системы измерения для углов. Также необходимо учитывать периодичность функции – после достижения пика, график повторяется.
Шаг 1: Определение амплитуды и периода

Амплитуда синусоиды представляет собой наибольшее значение функции на графике. Она равна половине разности максимального и минимального значений функции. Например, если максимальное значение функции равно 10, а минимальное значение равно -2, то амплитуда будет равна (10 - (-2))/2 = 6.
Период синусоиды является расстоянием между последовательными пиками или ямами на графике. Величина периода обозначается символом T и определяется по формуле T = 2π/|b|, где b - коэффициент перед переменной x в уравнении синусоиды. Например, если уравнение синусоиды имеет вид y = 5sin(2x), то период будет равен T = 2π/|2| = π.
С помощью найденной амплитуды и периода, можно построить график функции синусоиды с высотой пиков и ям, соответствующей амплитуде, и расстоянием между пиками и ямами, соответствующему периоду.
| Амплитуда | Период |
|---|---|
| 6 | π |
Шаг 2: Расчет значения функции для разных углов

Теперь, когда у нас есть основные представления о графике синусоиды, перейдем к расчету значения функции для разных углов.
Функция синуса (sin) определяется для всех реальных чисел. Однако, чтобы упростить задачу и сосредоточиться на наиболее распространенном случае, мы будем рассматривать расчет значения функции для углов, выраженных в радианах.
Для расчета значения функции синуса по графику нам потребуется знать значения функции для нескольких углов. Возьмем в качестве примера следующие углы: 0, π/6, π/4, π/3, и π/2.
0 радиан соответствует начальной точке графика, где функция синуса равна 0. По мере увеличения угла до π/2 радиан, значение функции синуса возрастает до максимального значения, равного 1. В промежутке между 0 и π/2 радиан значения функции синуса постепенно увеличиваются.
Чтобы рассчитать значения функции синуса для данных углов, мы можем использовать таблицу значений или специальные программы и калькуляторы. Например, для угла 0 радиан значение функции синуса будет равно 0, для угла π/6 радиан значение будет приближенно равно 0.5, для угла π/4 радиан значение будет приближенно равно 0.7071, для угла π/3 радиан значение будет приближенно равно 0.866 и для угла π/2 радиан значение будет равно 1.
Зная значения функции для этих углов, мы можем построить график синусоиды, соединяя соответствующие точки на графике синусоиды.
Шаг 3: Построение графика функции

После того как мы определили основные параметры функции синусоиды, мы можем перейти к построению её графика.
- На оси абсцисс (горизонтальной оси) откладываем значения аргумента функции. В данном случае это будет угол, который изменяется от 0 до 2π радиан.
- На оси ординат (вертикальной оси) откладываем значения функции синусоиды, которые получаются при подстановке соответствующих значений аргумента в функцию.
- Соединяем получившиеся точки графиком. Обратите внимание, что график будет иметь вид волнообразной кривой.
Для удобства можно использовать графические инструменты, такие как графические калькуляторы или программы для построения графиков функций. Они позволяют точно построить график и производить необходимые измерения и вычисления.
Также, помимо основного графика, можно добавить дополнительные элементы, такие как оси координат, деления и подписи для удобства интерпретации графика.
График функции синусоиды позволяет наглядно представить её поведение в зависимости от значения аргумента. Такой график позволяет проанализировать периодичность колебаний, амплитуду и фазовый сдвиг функции.
Построение графика функции синусоиды позволяет наглядно увидеть основные характеристики функции и использовать их в дальнейшем анализе и рассмотрении синусоидальных функций.
Шаг 4: Интерпретация графика и проверка
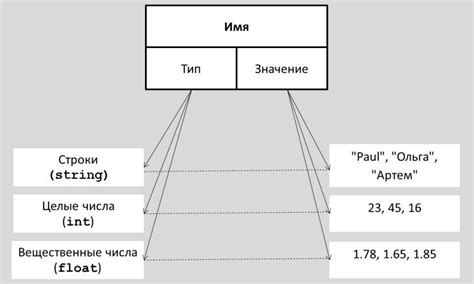
После того, как мы построили график синусоиды, следует правильно его интерпретировать и проверить полученные результаты.
Взглянув на график, мы видим, что функция имеет периодичность. Это означает, что она повторяется через определенные интервалы. На графике видно, что периодичность функции составляет 360 градусов или 2π радиан. Это объясняется тем, что синусоида является периодической функцией с периодом 2π.
Кроме того, мы также замечаем, что график симметричен относительно оси OY (ось ординат). Это свойство синусоиды известно как четность функции. Оно означает, что значения функции симметричны относительно оси OY. Например, синус(-x) = -синус(x).
Для большей проверки графика, мы можем выбрать некоторые точки и вычислить соответствующие значения функции синус. Например, при x = 0 радиан, значение синус равно 0. Это соответствует точке пересечения графика с осью Ox. При x = π/2 радиан, значение синус равно 1, что соответствует максимальному значению функции на графике.
Шаг 5: Добавление дополнительных параметров
При построении функции синусоиды можно использовать различные дополнительные параметры, чтобы настроить график под конкретные нужды.
Один из таких параметров - амплитуда (A). Амплитуда описывает насколько далеко график будет выходить из основной линии. Например, если задать амплитуду равную 1, график будет колебаться между значением -1 и 1. Если же амплитуда равна 2, график будет колебаться между -2 и 2.
Еще одним параметром является период (T) синусоиды. Период определяет, сколько времени требуется синусоиде, чтобы выполнить одну полную осцилляцию. Период обратно пропорционален частоте (f) синусоиды. Частота синусоиды обратно пропорциональна периоду.
- Установка большой амплитуды сделает график более высоким и ниже;
- Если изменить период, то график будет "растянут" или "сжат";
- Если изменить фазу, то вершина графика будет сдвинута влево или вправо;
- Для изменения высоты графика относительно начальной точки служит параметр сдвига (C) в уравнении синусоиды (y = A * sin(B * (x - C)) + D).
Используя эти дополнительные параметры, вы можете создавать синусоиды на основе различных моделей и настроек, чтобы визуализировать данные и создавать интересные графические эффекты.
Настройка этих параметров поможет вам создавать более сложные и интересные графики синусоиды, а также позволит адаптировать график под требуемые условия или потребности.