Диагонали квадрата – это линии, соединяющие противоположные вершины этой геометрической фигуры. Кажется, что они просто являются внутренними мерами, однако они несут в себе множество интересных свойств и характеристик, которые можно изучить, чтобы лучше понять и описать квадрат.
Одно из основных свойств диагоналей квадрата – равенство. Другими словами, диагонали квадрата имеют одинаковую длину и, соответственно, равняются между собой. Это свойство можно доказать с помощью геометрических построений или математическим путем, используя формулы и теоремы. Разберемся, как это работает.
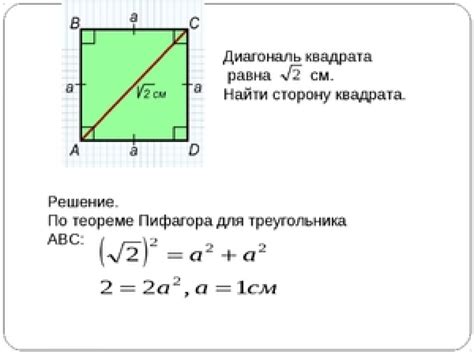
Возьмем квадрат со стороной "а". Пусть диагональ квадрата равна "d". Мы можем разложить стороны квадрата на составляющие и применить теорему Пифагора. Так как все стороны квадрата равны, мы получаем выражение: а² + а² = д². После простых алгебраических преобразований получаем: 2а² = д². Теперь найдем корень из обеих частей уравнения и получим следующее: √(2а²) = √(д²). Произведя несложные вычисления, получим окончательное равенство: √2 * а = д.
Что такое диагонали квадрата?

Каждая диагональ квадрата имеет свои характеристики и свойства:
1. Равенство диагоналей: Обе диагонали квадрата равны по длине. Это свойство является важным и отличает квадрат от других прямоугольников, у которых диагонали не равны.
2. Характеристики диагоналей: Каждая диагональ квадрата является диаметром вписанной окружности и разделяет квадрат на два равных прямоугольных треугольника. То есть, если знать длину диагонали, то можно вычислить радиус окружности, вписанной в квадрат, или наоборот - зная радиус окружности, можно вычислить длину диагонали.
3. Перпендикулярность: Диагонали квадрата пересекаются в его центре и образуют прямой угол, то есть они перпендикулярны друг другу.
4. Четверть окружности: Диагонали квадрата создают четверть окружности вокруг его центра. Если продолжить диагонали за пределы квадрата, то они будут пересекать границы окружности, получив четвертую часть окружности.
Диагонали квадрата играют важную роль при решении геометрических задач и вычислениях. Изучение и понимание свойств диагоналей помогает глубже познать особенности и характеристики квадрата.
Определение и понятие диагоналей
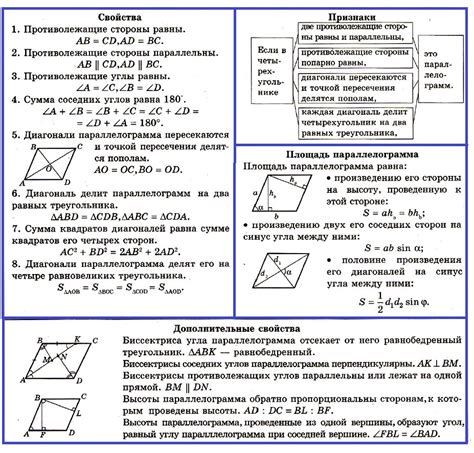
Диагонали квадрата обладают рядом особенных свойств. Одно из них - диагонали равны между собой. То есть, длина вертикальной диагонали равна длине горизонтальной диагонали. Это следует из симметрии квадрата относительно его диагоналей.
Другое важное свойство диагоналей квадрата заключается в их взаимном перпендикуляре. Вертикальная и горизонтальная диагонали квадрата являются перпендикулярными линиями, то есть, они пересекаются под прямым углом. Это свойство является следствием особой симметрии квадрата и его прямоугольной формы.
Диагонали квадрата также играют важную роль в вычислении его площади. Зная длину диагоналей, можно найти площадь квадрата по формуле: площадь = половина произведения длины вертикальной и горизонтальной диагоналей.
Изучение диагоналей квадрата помогает лучше понять эту фигуру и ее особенности. Значительная часть геометрических задач требует знания свойств и характеристик диагоналей квадратов, поэтому их изучение является важной частью образовательного процесса.
Как вычислить длину диагоналей?

Если известна длина стороны квадрата (a), длину диагоналей можно вычислить с помощью теоремы Пифагора.
Для вычисления длины диагоналей можно использовать следующие формулы:
| Формула | Длина диагонали |
|---|---|
| Диагональ AB | √2a |
| Диагональ AC | a√2 |
Где a – длина стороны квадрата.
Например, если сторона квадрата равна 4 см, то длина диагоналей будет:
Диагональ AB: √2 * 4 ≈ 5,65 см
Диагональ AC: 4 * √2 ≈ 5,65 см
Таким образом, для вычисления длины диагоналей квадрата необходимо знать длину его стороны и использовать соответствующие формулы.
Расчет длины диагоналей квадрата

Длина диагоналей квадрата может быть рассчитана с использованием его стороны. Для этого можно воспользоваться теоремой Пифагора, которая гласит: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов.
В случае квадрата, оба катета равны длине его стороны, а гипотенуза - длине диагонали. Таким образом, формула для расчета длины диагонали квадрата будет выглядеть следующим образом:
- Длина диагонали = √(сторона² + сторона²)
В простейшем случае, если известна длина стороны квадрата, можно просто подставить ее значение в формулу, чтобы рассчитать длину диагонали. Например, если сторона квадрата равна 5 см, то длина диагонали будет:
- Длина диагонали = √(5² + 5²) = √(25 + 25) = √50 ≈ 7.07 см
Таким образом, длина диагонали квадрата со стороной 5 см составляет около 7.07 см.
Зная формулу для расчета длины диагонали квадрата, можно также использовать ее для нахождения стороны квадрата, если известна длина диагонали. Для этого нужно просто переставить уравнение и решить его относительно стороны квадрата.
Таким образом, длина диагоналей квадрата можно рассчитать и использовать для нахождения других характеристик и свойств квадрата.
Свойства диагоналей квадрата
Диагонали квадрата – это отрезки, соединяющие противоположные вершины фигуры. Хотя диагонали не являются сторонами квадрата, они обладают рядом интересных и важных характеристик:
| Свойство диагоналей | Описание |
|---|---|
| Равенство диагоналей | В квадрате диагонали равны друг другу. |
| Симметричность диагоналей | Диагонали квадрата делят его на две равные части и являются осями симметрии. |
| Диагонали являются биссектрисами углов | Диагонали делят каждый угол квадрата пополам. |
| Диагонали перпендикулярны | Диагонали квадрата образуют прямой угол, то есть они перпендикулярны друг другу. |
Свойства диагоналей квадрата являются важными особенностями этой геометрической фигуры и используются во многих математических рассуждениях и доказательствах.
Взаимное расположение диагоналей
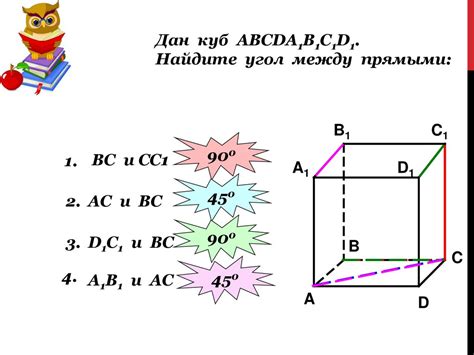
Диагонали квадрата имеют ряд особенностей и различные характеристики, в том числе и взаимное расположение. Давайте разберемся, как они расположены относительно друг друга.
Пересечение диагоналей – это точка, в которой они пересекаются. Эта точка делит каждую из диагоналей пополам и является центром вписанной окружности квадрата. Все четыре угла квадрата равны и составляют 90 градусов.
Каждая из диагоналей делит квадрат на два прямоугольных треугольника. В этих треугольниках одинаковыми являются углы, образованные диагональю и сторонами квадрата. Таким образом, «угол внизу» обоих треугольников – это прямой угол, равный 90 градусам.
В квадрате диагональ является главной диагональю, а другая диагональ называется побочной. Главная диагональ является биссектрисой угла между сторонами квадрата, то есть делит его на два равных треугольника.
Диагонали квадрата перпендикулярны друг другу, что означает, что они образуют прямой угол в точке их пересечения. Также они равны по длине – это следует из свойств главной и побочной диагоналей квадрата.
Таким образом, взаимное расположение диагоналей квадрата обладает рядом интересных свойств. Они пересекаются в точке, делят квадрат на четыре равных треугольника и образуют прямой угол. Знание этих особенностей поможет лучше понять геометрические свойства и характеристики квадрата.
Характеристики диагоналей квадрата
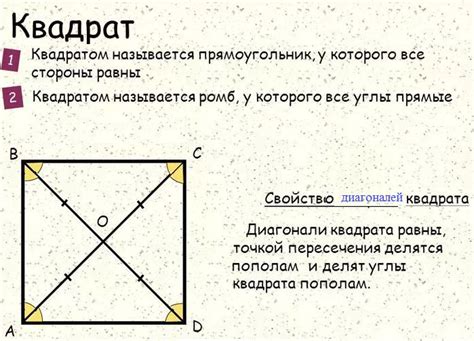
- Длина диагоналей: Длина каждой диагонали равна стороне квадрата, умноженной на корень из двух. Таким образом, если сторона квадрата равна a, то длина диагонали будет равна a * √2.
- Взаимное положение диагоналей: Диагонали квадрата являются взаимно перпендикулярными. Это означает, что они пересекаются под прямым углом.
- Симметричность: Диагонали квадрата симметричны относительно его центра. Это означает, что каждая диагональ делит весь квадрат на две равные части.
Знание характеристик диагоналей квадрата позволяет решать различные задачи в геометрии, такие как нахождение площади квадрата или определение его ориентации в пространстве.