Геометрия, многими считаемая скучной наукой, на самом деле полна неожиданностей и загадок. Одной из таких загадок является параллелограмм с биссектрисами углов. Эта форма, состоящая из двух параллельных сторон и двух параллельных диагоналей, обладает удивительными свойствами, особенно касаемо своих диагоналей.
Одно из самых интересных свойств такого параллелограмма связано с его диагоналями. Оказывается, что диагонали параллелограмма делятся друг другом в одном и том же отношении. Если обозначить точки пересечения диагоналей как A и B, то можно утверждать, что отношение длины отрезка AD к длине отрезка DB будет равно отношению длины отрезка AB к диагонали параллелограмма, состоящей из этих двух отрезков.
Необычность этой геометрической тайны заключается в том, что она применима к любому параллелограмму с биссектрисами углов, безотносительно его размеров и формы. Она открывает перед нами новые возможности для решения задач с использованием подобных фигур и является прекрасным примером того, как математика может быть красивой и удивительной.
Диагонали параллелограмма: формулы и свойства
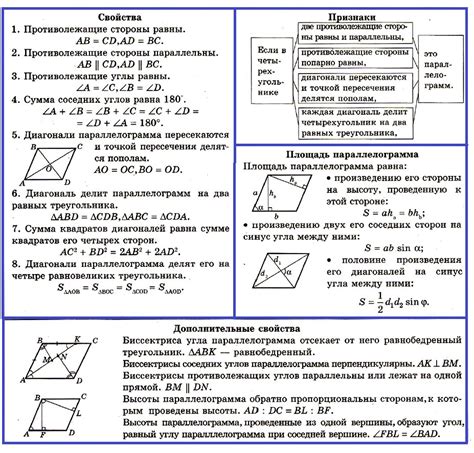
Одно из свойств диагоналей параллелограмма заключается в том, что они делят его на две равные части. То есть диагонали равны между собой по длине. Это свойство можно использовать для нахождения длин диагоналей параллелограмма, если известна длина одной из них.
Кроме того, можно выразить длину одной диагонали параллелограмма через его стороны и угол между ними. Для этого существует формула:
- Длина диагонали AB равна: d = √(a² + b² - 2abcos(α))
где a и b - стороны параллелограмма, α - угол между ними.
Диагонали параллелограмма также обладают следующими свойствами:
- Диагонали параллелограмма делят его на четыре треугольника, причем площадь каждого из этих треугольников равна половине площади параллелограмма.
- Если диагонали параллелограмма пересекаются в точке О, то точка О делит каждую диагональ на две равные части. То есть, отрезки AO=BO=CO=DO.
Биссектрисы углов и их роль

Для параллелограмма с биссектрисами углов характерны следующие свойства:
- Биссектрисы углов параллелограмма делят его на четыре треугольника, каждый из которых содержит одну из сторон параллелограмма и половину диагонали. Благодаря этому, свойства и отношения сторон и углов в этих треугольниках позволяют вывести множество равенств и соотношений для параллелограмма в целом.
- Биссектрисы представляют собой линии симметрии параллелограмма. Они делят его на две равные части, каждая из которых является зеркальным отражением другой.
- Пересечение биссектрис образует точку, которую в геометрии называют центром биссектрис. Она является точкой пересечения диагоналей параллелограмма и делит каждую из диагоналей на отрезки, длины которых могут быть выражены через стороны параллелограмма и углы.
Биссектрисы углов играют важную роль в геометрии параллелограмма, позволяя определить центры и соотношения между различными элементами этой фигуры. Изучение их свойств позволяет решать задачи, связанные с построением и вычислением параметров параллелограмма.