Гистограмма - это графическое представление распределения данных, которое широко используется в анализе и визуализации информации. Она позволяет наглядно представить, как часто встречаются различные значения переменной и показать их относительную частоту.
Однако, при работе с гистограммами иногда возникает необходимость повышения точности анализа. Для этого можно добавить на гистограмму график функции Гаусса, также известной как нормальное распределение или колоколообразное распределение.
Функция Гаусса описывает процесс, в котором большинство значений сконцентрировано вокруг среднего значения, а значения близкие к среднему имеют наибольшую вероятность. Такая функция имеет форму колокола и характеризуется двумя параметрами: средним значением и стандартным отклонением.
Раздел 1: Анализ гистограммы данных
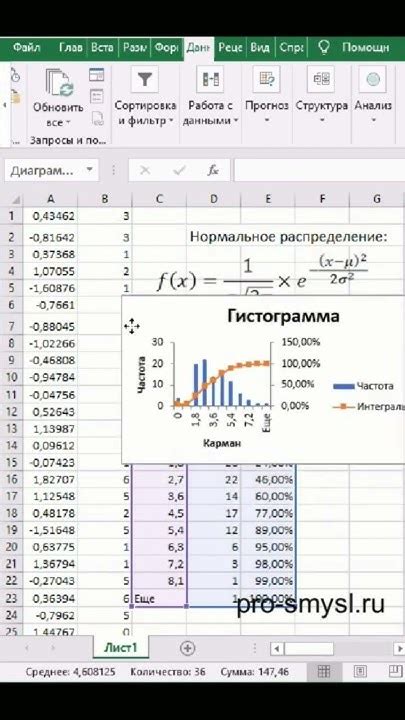
Анализ гистограммы данных является важным шагом при проведении статистического исследования или анализа данных. Позволяя определить основные характеристики выборки, гистограмма позволяет исследователю быстро и точно оценить какие-либо закономерности или аномалии в наборе данных.
Анализ гистограммы включает определение основных характеристик распределения данных: среднего значения, медианы, моды, дисперсии и стандартного отклонения. Кроме того, гистограмма позволяет увидеть насколько данные отклоняются от нормального распределения и выявить наличие выбросов.
| Характеристика | Описание |
|---|---|
| Среднее значение | Среднее арифметическое всех значений в наборе данных |
| Медиана | Центральное значение, которое делит выборку пополам |
| Мода | Самое часто встречающееся значение в наборе данных |
| Дисперсия | Степень разброса значений в наборе данных относительно среднего значения |
| Стандартное отклонение | Показатель разброса значений в наборе данных относительно среднего значения |
Используя гистограмму, аналитик может выявить закономерности в данных, такие как скошенность (асимметрия) распределения влево или вправо, а также выявить форму распределения - нормальное, экспоненциальное, равномерное и т. д.
Анализ гистограммы данных является важным этапом в процессе исследования и анализа данных, позволяющим получить максимально точное представление о закономерностях и характеристиках выборки.
Раздел 1.1: Определение гистограммы и ее важность

Гистограммы имеют широкое применение в статистике и анализе данных. Они позволяют визуализировать распределение значений и обнаружить особенности данных, такие как моды, выбросы или скосы. Поэтому гистограммы являются незаменимым инструментом в исследовании данных, построении прогнозов и принятии решений на основе данных.
Раздел 1.2: Проблемы точности в анализе гистограммы
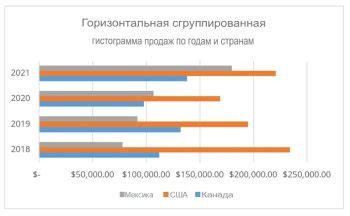
При построении гистограммы выделяется фиксированное количество интервалов, которые разделяют диапазон значений данных. Каждый интервал представляет собой отдельный столбец на гистограмме, и его высота соответствует количеству значений, попадающих в этот интервал.
Однако, если данные имеют достаточно большой разброс или неоднородность распределения, фиксированное количество столбцов может привести к потере значимой информации. Фактически, если данные слишком малочисленны, интервалы на гистограмме могут быть пустыми или содержать очень мало значений, что может исказить представление о распределении данных.
Для повышения точности анализа гистограммы можно использовать функцию Гаусса. Функция Гаусса, также известная как нормальное распределение или колоколообразное распределение, позволяет сгладить гистограмму и приблизить ее к истинному распределению данных.
Применение функции Гаусса к гистограмме позволяет увидеть более плавное и непрерывное распределение данных, даже если в исходных данных есть выбросы или неоднородности. Это особенно полезно при анализе больших объемов данных или в случаях, когда точность анализа играет важную роль.
Раздел 2: Функция Гаусса для повышения точности анализа
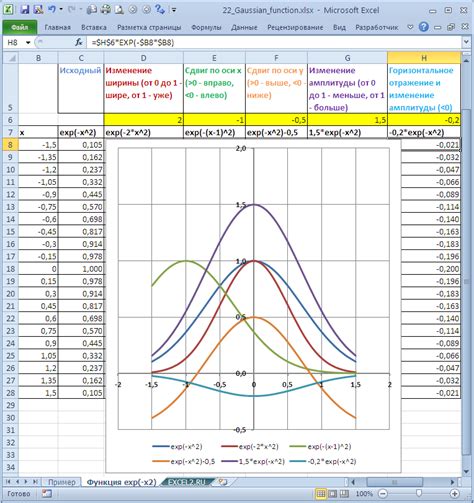
Добавление функции Гаусса на гистограмму позволяет учесть закономерности в распределении данных. Функция Гаусса имеет колоколообразную форму и определяется двумя параметрами - средним значением и стандартным отклонением. С помощью этих параметров можно изменять форму функции Гаусса и достигать лучшей соответствия данных.
При добавлении функции Гаусса на гистограмму происходит сглаживание данных, что позволяет выявить более тонкие закономерности и различия между значениями. Это особенно полезно, если распределение данных имеет выраженные пики или хвосты.
Раздел 2.1: Описание функции Гаусса
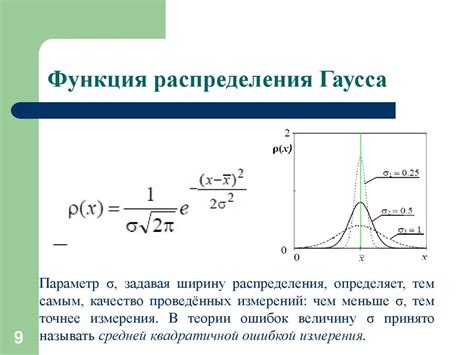
Функция Гаусса определяется следующим образом:
$$
f(x) = \frac{1}{{\sqrt{2\pi}\sigma}}e^{-\frac{(x - \mu)^2}{2\sigma^2}}
$$
где:
- - \(x\) - значение переменной,
- - \(\mu\) - математическое ожидание (среднее значение),
- - \(\sigma\) - стандартное отклонение.
Основная черта функции Гаусса - её симметричность относительно пика в точке \(\mu\). Отклонение от этой точки определяется стандартным отклонением \(\sigma\). Чем меньше значение \(\sigma\), тем более "острый" и высокий становится пик функции, и наоборот.
Для добавления функции Гаусса на гистограмму необходимо найти оптимальные значения \(\mu\) и \(\sigma\), которые наилучшим образом соответствуют данным. Это может быть сделано с использованием метода максимального правдоподобия или других статистических методов.
Раздел 2.2: Применение функции Гаусса на гистограмму
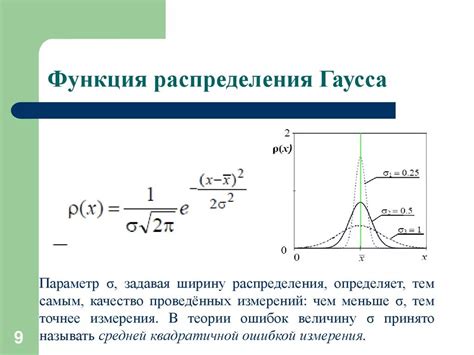
Применение функции Гаусса на гистограмму позволяет сгладить ее форму и уменьшить воздействие выбросов или случайных шумов на результаты анализа данных. Это особенно полезно в случаях, когда гистограмма имеет резкие пики или явные длинные хвосты, которые мешают получить более точные результаты.
Для применения функции Гаусса на гистограмму необходимо произвести следующие шаги:
| Шаг | Описание |
|---|---|
| 1 | Рассчитать среднее значение и стандартное отклонение данных, представленных на гистограмме. |
| 2 | Используя среднее значение и стандартное отклонение, построить функцию Гаусса, которая будет аппроксимировать данные на гистограмме. |
| 3 | Нанести функцию Гаусса на гистограмму для визуального сравнения и оценки различий между аппроксимированными данными и реальной гистограммой. |
| 4 |
Такой подход позволяет уменьшить случайные искажения и сделать анализ данных более точным и репрезентативным. Однако следует помнить, что применение функции Гаусса на гистограмму также может иметь свои ограничения и пределы применимости, особенно в случаях, когда данные имеют скрытые ограничения или несимметричное распределение.
Раздел 3: Повышение точности без лишней сложности

При добавлении функции Гаусса на гистограмму происходит сглаживание данных и устранение выбросов, что позволяет более точно определить характеристики распределения. Это особенно важно в случаях, когда данные имеют явно выраженный пик или длинный хвост, что может исказить результаты анализа.
Основная идея добавления функции Гаусса на гистограмму заключается в том, что каждый столбец гистограммы заменяется функцией Гаусса с центром, соответствующим значению столбца. Таким образом, данные сглаживаются и получается более плавный график, более точно отражающий характеристики распределения.
Для добавления функции Гаусса на гистограмму можно использовать специальные программные инструменты, такие как Python с библиотекой matplotlib или R с пакетом ggplot2. Эти инструменты предоставляют широкие возможности для настройки параметров функции Гаусса и создания точных и выразительных графиков.
Раздел 3.1: Преимущества использования функции Гаусса
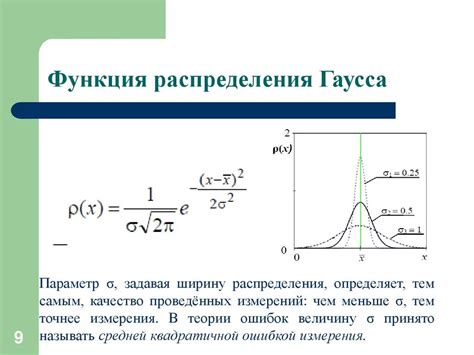
Во-первых, функция Гаусса позволяет более точно аппроксимировать распределение данных, особенно в случаях, когда оно имеет "колоколообразную" форму. Гауссова функция обладает плавными и симметричными краями, что позволяет лучше представить данные и определить точные значения пиков и хвостов распределения.
Во-вторых, функция Гаусса позволяет учесть шум и случайность данных, позволяя снизить вероятность ложных срабатываний. Благодаря своей гладкой форме, Гауссова функция усредняет значения данных вокруг пика, что позволяет уменьшить влияние случайных выбросов и повысить точность анализа.
Кроме того, преимуществом использования функции Гаусса является возможность более точно настроить параметры аппроксимации. Можно изменять ширину и положение пика функции, варьируя значениями среднего и стандартного отклонения, что позволяет лучше подстроить ее под конкретные данные и повысить точность анализа гистограммы.
Таким образом, использование функции Гаусса на гистограмме предоставляет ряд преимуществ, включая более точную аппроксимацию распределения данных, учет шума и повышение точности анализа. Это позволяет получить более надежные результаты и улучшить качество анализа без добавления лишней сложности.