Фибоначчи - одна из самых известных последовательностей чисел, которая является основой для множества математических и прикладных задач. Популярность этой последовательности обусловлена её математическими свойствами, а также её применимостью во многих областях жизни. Однако, помимо Фибоначчи, существуют и другие последовательности чисел, которые строятся на подобных принципах. В данной статье речь пойдет о двух таких последовательностях, Трибоначчи и Тетраначчи, и их особенностях и применении.
Последовательности Фибоначчи, Трибоначчи и Тетраначчи все основываются на одной и той же идее - последующее число в последовательности получается как сумма нескольких предыдущих чисел этой же последовательности. В случае Фибоначчи, каждое число является суммой двух предыдущих чисел, в то время как Трибоначчи - суммой трех, и Тетраначчи - суммой четырех. Таким образом, данные последовательности можно определить следующим образом:
Фибоначчи: F(n) = F(n-1) + F(n-2)
Трибоначчи: T(n) = T(n-1) + T(n-2) + T(n-3)
Тетраначчи: Te(n) = Te(n-1) + Te(n-2) + Te(n-3) + Te(n-4)
Интересно отметить, что Фибоначчи последовательность возникла еще в древности и была открыта итальянским математиком Леонардо Пизанским, известным также как Фибоначчи. Однако, последующие имена, такие как Трибоначчи и Тетраначчи, появились уже в более поздние времена, в рамках развития исследований в области комбинаторики и математического программирования.
Также стоит отметить, что данные последовательности имеют широкий спектр применимости в различных областях науки и техники, включая финансовый анализ, анализ временных рядов, кодирование, генетику и даже музыку. Изучение особенностей и применения таких последовательностей чисел позволяет получить глубокое понимание их математической сути и использовать их в решении сложных задач в разных областях науки и техники.
Фибоначчи - основа числовой последовательности

Формула для вычисления числа Фибоначчи может быть записана следующим образом:
Fn = Fn-1 + Fn-2
где Fn - n-ое число Фибоначчи, Fn-1 - (n-1)-ое число Фибоначчи, Fn-2 - (n-2)-ое число Фибоначчи.
Некоторые начальные значения последовательности:
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Последовательность Фибоначчи имеет множество интересных и свойственных ей характеристик, которые нашли свое применение в различных науках и областях. Эта последовательность является фундаментальной для различных алгоритмов, информационной теории, физики и даже искусства.
Различные подходы к построению
При построении дополнительных имен Фибоначчи существуют разные подходы, которые можно использовать в зависимости от конкретных задач.
Один из подходов - это построение Трибоначчи. В этом случае последовательность начинается с трех чисел, а каждое следующее число является суммой трех предыдущих. То есть: T(n) = T(n-1) + T(n-2) + T(n-3). Такой подход может быть полезен, когда необходимо учитывать более широкий контекст данных и предсказывать тренды в долгосрочной перспективе.
Еще один подход - это построение Тетраначчи. В этом случае последовательность начинается с четырех чисел, а каждое следующее число является суммой четырех предыдущих: Te(n) = Te(n-1) + Te(n-2) + Te(n-3) + Te(n-4). Этот подход может быть полезен, когда необходимо учитывать еще больший контекст данных и предсказывать более сложные или долгосрочные тренды.
Однако следует отметить, что использование дополнительных имен Фибоначчи может быть ограничено, и не всегда эти подходы окажутся эффективными или применимыми в конкретных ситуациях. Для каждой задачи необходимо тщательно анализировать данные и выбирать соответствующий подход.
Особенности Фибоначчи
Особенности Фибоначчи:
1. Золотое сечение. В ряде Фибоначчи отношение каждого числа к предыдущему стремится к постоянному числу, которое называется "золотым сечением" (приближенное значение равно 1,6180339887...). Золотое сечение является математическим понятием, которое встречается в искусстве, архитектуре и природе. Оно считается пропорцией, придающей объектам гармоничный и привлекательный вид.
2. Фракталы. Ряд Фибоначчи обладает фрактальными свойствами, что означает, что его можно повторять в бесконечность и все равно получать схожую себе картину. Фракталы Фибоначчи находят применение в компьютерной графике, дизайне, создании графических паттернов и текстур.
3. Волновой анализ. Фибоначчиевы числа широко применяются в анализе графиков и трендов. Волновой анализ, основанный на Фибоначчиевом ряде, помогает определить возможное развитие ценовых движений на финансовых рынках. Это важный инструмент для трейдеров и инвесторов.
Таким образом, ряд Фибоначчи обладает рядом особенностей, которые делают его уникальным и широко применимым в различных сферах человеческой деятельности.
Трибоначчи - расширение Фибоначчи

То есть, начиная с первых трех чисел: 0, 0, 1, каждое последующее число в Трибоначчи будет равно сумме трех предыдущих чисел.
- Первые 10 чисел последовательности Трибоначчи: 0, 0, 1, 1, 2, 4, 7, 13, 24, 44.
- Следующие числа последовательности Трибоначчи: 81, 149, 274, 504, 927, и так далее.
Трибоначчи также имеет свои специальные свойства и приложения в различных областях. Например, она может быть использована для решения задач, связанных с моделированием популяции организмов или математическим анализом алгоритмов.
Последовательность Трибоначчи также может быть использована для генерации уникальных ключей или идентификаторов, поскольку она обладает высокой степенью псевдослучайности и непредсказуемости.
Как получить Трибоначчи
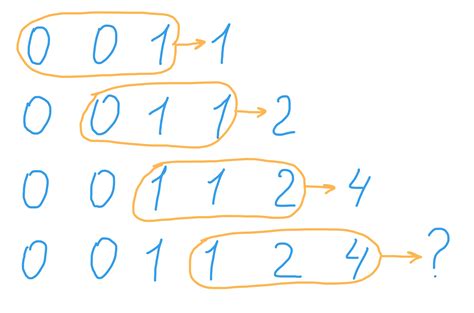
Для получения Трибоначчи можно использовать рекурсивный или итеративный алгоритм. В рекурсивном алгоритме функция вызывает саму себя, чтобы найти следующий элемент Трибоначчи. В итеративном алгоритме используется цикл, чтобы находить элементы последовательности до требуемого индекса.
Вот пример кода на языке Python, который позволяет получить Трибоначчи:
def tribonacci(n):
if n == 0:
return 0
elif n == 1 or n == 2:
return 1
else:
a, b, c = 0, 1, 2
for _ in range(n - 2):
a, b, c = b, c, a + b + c
return c
n = 10
result = tribonacci(n)
В этом примере функция tribonacci(n) принимает целое число n в качестве аргумента и возвращает соответствующий элемент Трибоначчи. Результат работы функции для n = 10 равен 149.
Трибоначчи имеет ряд интересных свойств и может быть использовано, например, для решения задач на программирование или в алгоритмах оптимизации.
Применение Трибоначчи
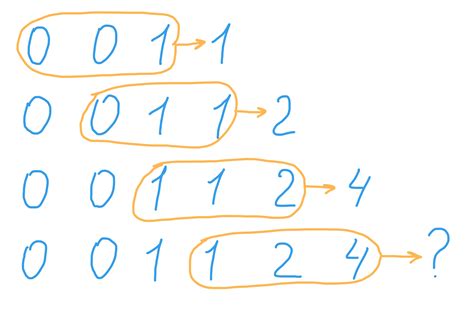
Дополнительная последовательность чисел Фибоначчи, известная как Трибоначчи, находит применение в различных областях. Вот некоторые из них:
1. Алгоритмы и программирование:
Последовательность Трибоначчи может быть использована для создания эффективных алгоритмов, основанных на рекурсии или динамическом программировании. Эта последовательность может быть использована для решения задач, связанных с оптимизацией и поиском оптимальных решений.
2. Криптография:
Трибоначчи может быть использована в криптографии, где она может служить базой для создания криптографических алгоритмов и техник шифрования. Это связано с ее уникальными свойствами в генерации случайных чисел и сложности обратного отслеживания.
3. Финансовая математика:
Последовательность Трибоначчи может быть использована для моделирования и прогнозирования финансовых рынков, а также для анализа временных рядов и ценовой динамики. Ее уникальная структура и свойства могут помочь в определении трендов, циклов и аномалий на рынке.
4. Биология и генетика:
Последовательность Трибоначчи может быть использована для анализа генетической информации и оценке вероятности возникновения определенных генетических последовательностей. Она может быть применена как инструмент для исследования геномов и передачи наследственности.
Таким образом, последовательность Трибоначчи имеет широкий спектр применений и играет важную роль в различных областях. Ее уникальные свойства и рекурсивная структура делают ее полезной и мощной математической конструкцией.