Эффективные методы нахождения корня числа без калькулятора

Вычисление корня числа является одной из фундаментальных операций в математике. Она используется во многих областях, включая физику, инженерию, экономику и другие. Часто возникает необходимость найти корень числа без использования калькулятора. В таких случаях необходимы эффективные методы расчета, которые позволяют получить приближенное значение корня с высокой точностью.

Один из наиболее популярных методов нахождения корня числа – метод Ньютона. Он основан на итерационном процессе, в ходе которого последовательно уточняется значение корня. Суть метода заключается в поиске точки пересечения касательной к графику функции с осью абсцисс. По мере приближения к истинному значению корня, разница между полученным и ожидаемым значением уменьшается.

Другим распространенным методом нахождения корня числа является метод деления отрезка пополам. Он основан на принципе половинного деления и позволяет быстро находить приближенное значение корня. Суть метода заключается в установлении границы интервала, в котором находится корень, и последующем его последовательном уточнении путем деления интервала пополам.

Независимо от выбранного метода, нахождение корня числа без калькулятора требует тщательного анализа и вычислительной работы. Эффективные методы позволяют получить точное или приближенное значение корня с минимальной погрешностью. Они являются неотъемлемой частью математических и инженерных вычислений, а также находят применение в различных областях науки и техники.

Методы нахождения корня числа без калькулятора

Нахождение корня числа без калькулятора может быть полезным навыком, особенно при выполнении математических расчетов вручную или при отсутствии доступа к калькулятору. В этом разделе мы рассмотрим несколько эффективных методов нахождения корня числа без использования калькулятора.

1. Метод приближения.

Выберите начальное приближение числа, которое близко к искомому корню.
Повторяйте следующий шаг до тех пор, пока полученное приближение не будет достаточно близко к искомому корню:

Рассчитайте новое приближение, используя следующую формулу: новое приближение = (предыдущее приближение + (число / предыдущее приближение)) / 2.

2. Метод деления и умножения.

Выберите начальное приближение числа, которое близко к искомому корню.
Повторяйте следующий шаг до тех пор, пока полученное приближение не будет достаточно близко к искомому корню:

Рассчитайте новое приближение, используя следующую формулу: новое приближение = (предыдущее приближение + (число / предыдущее приближение)) / 2.
Проверьте, близко ли полученное приближение к искомому корню, и скорректируйте его, если необходимо.
Повторяйте шаги 2 и 3 до тех пор, пока полученное приближение не будет достаточно близко к искомому корню.

3. Метод итераций.

Выберите начальное приближение числа, которое близко к искомому корню.
Рассчитайте новое приближение, используя следующую формулу: новое приближение = предыдущее приближение - (предыдущее приближение^2 - число) / (2 * предыдущее приближение).
Повторяйте шаг 2 до тех пор, пока полученное приближение не будет достаточно близко к искомому корню.

Ниже приведен пример использования этих методов:


function findSquareRoot(number) {
// Методы нахождения корня числа без калькулятора
// ...
}
const number = 16;
const squareRoot = findSquareRoot(number);
console.log("Корень числа " + number + " равен " + squareRoot);

Используя эти методы, вы сможете находить корень числа без калькулятора с высокой точностью. Помните только, что для получения точного значения корня может потребоваться больше итераций и более тщательный подбор начального приближения.

Метод окружения корня

Для начала выбирается диапазон, в котором предполагается находится искомый корень. Затем производится последовательное окружение числа, изменяя его значение в указанном диапазоне. При каждой итерации происходит проверка, находится ли искомый корень в окружении числа.

Процесс окружения корня может быть осуществлен различными способами, в зависимости от вида числа и требуемой точности. Возможно использование метода деления пополам, метода простой итерации или других подходов.

Окончание процесса нахождения корня обычно происходит при достижении заданной точности или при выполнении определенного критерия остановки. Это позволяет найти приближенное значение корня числа, которое может быть использовано в дальнейших вычислениях или анализе данных.

Метод окружения корня является эффективным инструментом для нахождения корня числа без использования калькулятора. Он позволяет получить достаточно точное значение корня и может быть использован в различных областях науки и техники.

Метод деления отрезка пополам

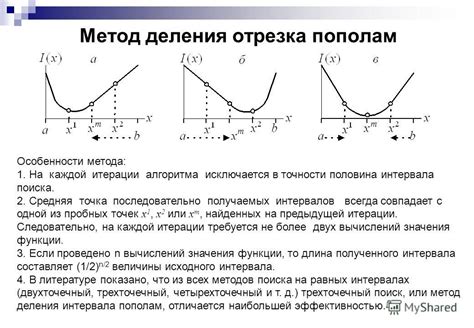
Алгоритм метода заключается в следующем:

Выбирается начальный отрезок, внутри которого находится корень уравнения.
Отрезок делится пополам и определяется его середина.
Значение функции в середине отрезка сравнивается с нулем.
В зависимости от полученного результата выбирается новый отрезок, внутри которого находится корень уравнения.
Повторяются шаги 2-4 до тех пор, пока не будет достигнута необходимая точность.

Метод деления отрезка пополам позволяет эффективно находить корни уравнений разных типов, включая квадратные и трансцендентные уравнения. Он прост в реализации и не требует большого объема вычислений.

Однако следует учитывать, что метод деления отрезка пополам не гарантирует точное нахождение корня уравнения, а лишь приблизительное значение. Для достижения большей точности может потребоваться увеличение числа итераций и уменьшение размера отрезка.