Диагональ круга – это одна из важнейших характеристик, определяющих геометрические параметры данной фигуры. Узнать ее значение можно с помощью простой формулы, основанной на диаметре круга. Знание диагонали круга может быть полезно во многих сферах практической деятельности, включая архитектуру, строительство или просто изучение геометрии. В данной статье мы подробно рассмотрим, как быстро и легко найти диагональ круга по его диаметру.
Диагональ круга – это отрезок, соединяющий две точки на периметре фигуры, не связанные смежной линией или радиусом. Обычно, для обозначения диагонали используется символ "d". По определению, диагональ проходит через центр круга и является максимальным отрезком, который можно провести внутри данной фигуры.
Найти диагональ круга по диаметру можно с помощью простой и удобной формулы. Диаметр круга – это отрезок, соединяющий две его точки на противоположных сторонах. Обозначается он символом "D". Диаметр равен удвоенному радиусу фигуры ("R"). Таким образом, формула для вычисления диагонали круга выглядит следующим образом: d = D * √2 / 2. Давайте разберемся, как эта формула работает на практике.
Как найти диагональ круга по диаметру
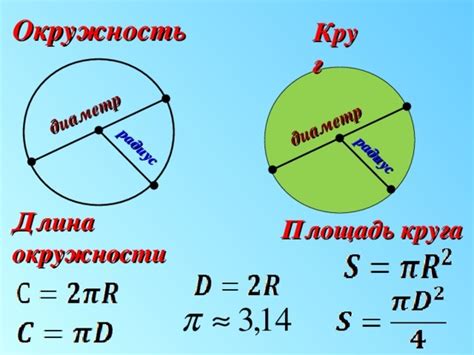
Диаметр круга - это отрезок, проходящий через центр круга и соединяющей его две противоположные точки на окружности.
Зная диаметр круга, можно легко найти его диагональ.
Для этого нам понадобится знание основного свойства круга, связанного с диаметром.
Известно, что диаметр круга является максимальным отрезком на окружности.
Полуразмер диагонали равен полуразмеру диаметра, так как они соединяют одни и те же точки на окружности.
Таким образом, диагональ круга равна двум радиусам или равна диаметру, то есть двукратное значение радиуса.
Формула для нахождения диагонали круга по диаметру будет следующей:
- Найдите диаметр круга;
- Умножьте диаметр на 2;
- Получите значение диагонали круга.
Примером будет ситуация, где диаметр равен 8 см. Умножив его на 2, получим диагональ круга, равную 16 см.
Или же можно использовать формулу в обратном направлении, если известна диагональ, то для нахождения диаметра нужно поделить значение диагонали на два.
Таким образом, если диагональ равна 16 см, то диаметр будет равен 8 см.
Теперь уже можно с легкостью найти диагональ круга, зная его диаметр.
Это очень полезное знание при работе с геометрией или при решении задач построения и измерения окружностей.
Не забудьте учесть указанные формулы, чтобы быстро и точно определить диагональ круга по его диаметру.
Методы расчета диагонали круга

- Используя радиус и угол
- Используя диаметр
- Используя площадь
- Используя длину окружности
- Используя площадь сектора
В этом методе для расчета диагонали круга необходимо знать его радиус и угол, на который эта диагональ отклоняется от горизонтали. Для нахождения диагонали можно воспользоваться формулой:
диагональ = 2 * радиус * sin(угол/2)
Простейшим способом найти диагональ круга является использование его диаметра. Диаметр - это отрезок, соединяющий две точки на периметре круга, проходящий через его центр. Для нахождения диагонали круга по диаметру можно воспользоваться формулой:
диагональ = диаметр
Еще одним методом расчета диагонали круга является использование его площади. Для нахождения диагонали круга по площади можно воспользоваться формулой:
диагональ = √(4 * площадь / π)
Длина окружности - это периметр круга. Для расчета диагонали круга по длине окружности можно воспользоваться формулой:
диагональ = длина окружности / π
Если известна площадь сектора круга и угол, на который этот сектор отклоняется от горизонтали, то можно найти диагональ круга по формуле:
диагональ = 2 * √(площадь сектора * sin(угол/2) / π)
Выше представлены основные методы для расчета диагонали круга. Независимо от выбранного метода, важно учесть единицы измерения, заданные для входных данных и полученного результата.
Практическое применение формулы

Формула для нахождения диагонали круга по диаметру имеет широкое практическое применение в различных областях. Некоторые из них:
- Строительство: при проектировании зданий и сооружений часто требуется учитывать диагональ круга, например, при расчётах необходимого пространства для размещения оборудования или при определении геометрических параметров архитектурных элементов.
- Машиностроение: при разработке и конструировании различных механизмов и устройств часто возникает необходимость знать диагональ круга, например, при расчёте габаритов механизмов или при определении геометрических параметров деталей.
- Визуальные искусства: при создании иллюстраций, графики, дизайна и других произведений искусства диагональ круга может использоваться для создания гармоничных композиций и пропорций.
- Образование и наука: формула для нахождения диагонали круга по диаметру является одним из базовых математических знаний и широко используется при изучении геометрии и алгебры.
В целом, знание формулы для нахождения диагонали круга по диаметру позволяет решать разнообразные практические задачи, связанные с геометрией и техническими расчётами, и может быть полезным в различных профессиональных областях.