Эйлео — внимание всего мира привлекает алгоритм глубокого обучения

Эйлер - это удивительный алгоритмический принцип, который широко применяется в различных областях науки и техники. Разработанный великим математиком Леонардом Эйлером, этот принцип позволяет решать сложные задачи с помощью простых алгоритмов.

Суть принципа работы эйлера заключается в разбиении сложной задачи на более простые подзадачи. Затем решение этих подзадач комбинируется, чтобы получить полное решение исходной задачи. Такой подход позволяет существенно упростить решение сложных проблем.

Преимущества принципа работы эйлера весьма значительны. Во-первых, он позволяет решать сложные задачи с использованием простых и понятных алгоритмов. Это делает его доступным для широкой аудитории и позволяет применять его в различных областях.

Во-вторых, принцип работы эйлера является эффективным способом решения проблем. Благодаря разбиению задачи на подзадачи и последующему комбинированию их решений, принцип позволяет получить оптимальное решение исходной задачи. Это особенно важно в задачах, где время и эффективность играют решающую роль.

Принцип работы алгоритма Эйлера:

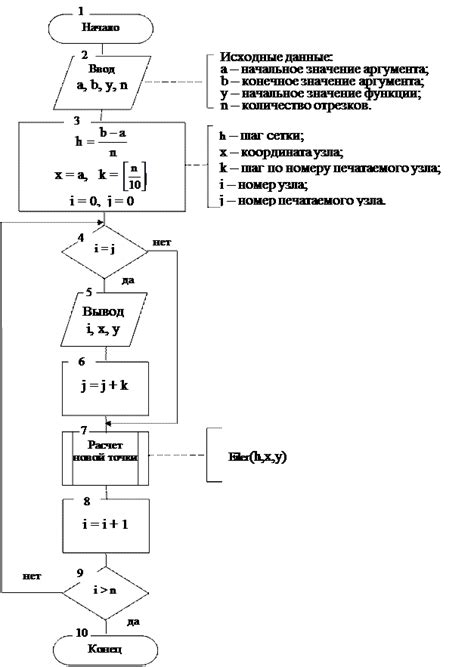
Алгоритм Эйлера, также известный как алгоритм обхода Эйлера или алгоритм обхода графа, представляет собой метод нахождения эйлерова цикла в заданном графе. Эйлеровым циклом называется замкнутый путь, проходящий по всем ребрам графа и возвращающийся в исходную точку, при этом каждое ребро используется только один раз.

В основе алгоритма Эйлера лежит следующая идея: если в графе существует эйлеров цикл, то каждая вершина графа имеет четную степень. Это означает, что из каждой вершины можно выйти и в неё можно прийти по ребрам графа. При этом, алгоритм Эйлера позволяет найти не только эйлеров цикл, но и эйлеров путь, который является аналогом цикла, но может иметь начальную и конечную вершины, которые не совпадают.

Принцип работы алгоритма Эйлера заключается в следующих шагах:

1. Выбрать произвольную вершину графа в качестве текущей вершины.
2. Пока текущая вершина имеет исходящие ребра:

• Выбрать произвольное исходящее ребро из текущей вершины.
• Перейти в другую вершину, соединенную с текущей выбранным ребром.
• Удалить выбранное ребро из графа.
• Установить новую текущую вершину.

Таким образом, алгоритм Эйлера позволяет найти эйлеров цикл или путь в графе, если он существует. Если граф не содержит вершин нечетной степени и является связным, то он обязательно содержит эйлеров цикл. Если граф содержит две вершины нечетной степени, то он содержит эйлеров путь. Если в графе есть вершина с нечетной степенью, а остальные вершины имеют четные степени, то эйлеровых циклов и путей не существует.

Изначальная задача и описание алгоритма

Принцип работы эйлерова алгоритма основан на решении специального класса математических задач, связанных с графами. Изначально рассматриваемая задача заключается в нахождении эйлерова цикла или пути в графе.

Эйлеров цикл представляет собой замкнутый путь, проходящий по каждому ребру графа ровно один раз. Эйлеров путь, в свою очередь, проходит по каждому ребру графа ровно один раз, но может быть не замкнутым.

Алгоритм Эйлера предназначен для решения этой задачи и состоит из следующих шагов:

1. Выбрать произвольную вершину графа.
2. Пройти по ребру из выбранной вершины в соседнюю вершину, удалить данное ребро из графа.
3. Повторить предыдущий шаг для новой вершины, пока они не закончатся.
4. Если все ребра графа были удалены, полученный путь будет эйлеровым путем или циклом.

Эйлеров алгоритм обладает рядом преимуществ, таких как:

• Простота реализации и понимания алгоритма.
• Гарантированная корректность решения, если граф является связным.
• Эффективность работы, время работы алгоритма пропорционально числу ребер и вершин графа.

Анализ комплексности и оптимизации алгоритма

При использовании алгоритма Эйлера необходимо провести анализ его комплексности и определить возможности оптимизации.

Комплексность алгоритма Эйлера определяется количеством ребер и вершин в графе. В общем случае, сложность алгоритма Эйлера составляет O(V+E), где V - количество вершин, а E - количество ребер.

Оптимизировать алгоритм Эйлера можно различными способами. Во-первых, можно использовать более эффективные структуры данных для хранения графа, такие как список смежности или матрица смежности. Это позволит уменьшить время работы алгоритма и использовать меньше памяти.

Во-вторых, можно применить различные эвристики и оптимизации для поиска эйлеровых путей. Например, можно использовать жадные алгоритмы, которые выбирают наиболее перспективные ребра или вершины на каждом шаге построения пути.

Также стоит учитывать особенности конкретной задачи и графа. Например, если граф сильно связный, то можно использовать алгоритмы обхода в глубину или обхода в ширину для построения эйлерового пути.

Важно отметить, что оптимизация алгоритма Эйлера может привести к уменьшению временной сложности, но при этом может увеличить сложность реализации и поддержки алгоритма.

В целом, применение алгоритма Эйлера требует внимательного анализа комплексности и возможной оптимизации, чтобы найти баланс между производительностью и сложностью алгоритма.

Универсальность и гибкость алгоритма

Одно из преимуществ эйлерова метода заключается в его способности обрабатывать сложные системы с нелинейными уравнениями. Этот алгоритм позволяет аппроксимировать решение системы дифференциальных уравнений с высокой точностью, даже если аналитическое решение неизвестно или сложно получить. Эйлеров метод легко адаптируется для работы с любыми типами дифференциальных уравнений, что делает его универсальным инструментом в научной и инженерной работе.

Гибкость алгоритма Эйлера заключается в его возможности изменять шаг интегрирования и точность вычислений. Это позволяет исследователям более точно настраивать алгоритм под конкретную задачу и получать нужные результаты. Также, изменение шага интегрирования позволяет контролировать время вычислений и оптимизировать процесс моделирования. Он также может быть легко модифицирован для решения разных типов задач, добавления новых параметров или условий.

В целом, универсальность и гибкость алгоритма Эйлера делают его незаменимым инструментом для работы с дифференциальными уравнениями и моделирования сложных систем. С его помощью исследователи и инженеры могут проводить широкий спектр исследований и получать точные результаты в краткие сроки.

Преимущества применения алгоритма Эйлера

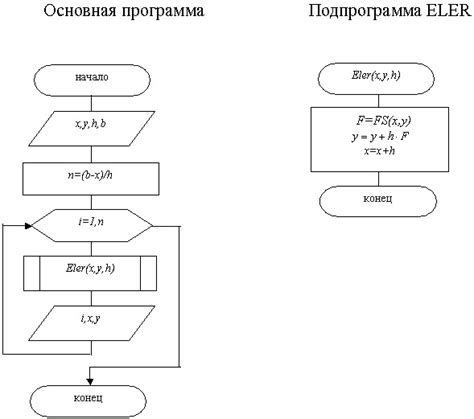
1. Простота реализации и понимания. Алгоритм Эйлера основан на простых правилах и не требует особых навыков программирования для его применения.

2. Эффективность. Алгоритм Эйлера позволяет находить эйлеровы циклы и пути в графах с линейной сложностью, что позволяет решать задачи большого масштаба за разумное время.

3. Универсальность. Алгоритм Эйлера может быть использован в различных областях, где необходимо находить гамильтоновы циклы или пути, таких как транспортная логистика, сетевые анализы и т.д.

4. Решение множества задач. Алгоритм Эйлера не только находит эйлеровы циклы и пути, но и может быть адаптирован для решения других задач, связанных с графами, таких как поиск кратчайших путей или схемы.

Применение алгоритма Эйлера в практических задачах помогает достичь эффективного и точного результата, а также существенно сокращает время обработки данных.

Возможное применение алгоритма в различных областях

Алгоритм Эйлера может быть применен во многих областях, благодаря своей простоте и эффективности. Рассмотрим некоторые из них:

1. Транспортная сеть: алгоритм Эйлера может быть использован для определения оптимального маршрута при доставке грузов или пассажиров. Он позволяет найти замкнутый путь, который проходит через каждую дорогу или трассу только один раз.
2. Биоинформатика: Эйлеровы пути часто используются для сборки и анализа геномов. Алгоритм помогает определить последовательность областей ДНК или РНК, а также установить связи между ними.
3. Социальные сети: алгоритм Эйлера может использоваться для анализа взаимосвязей между людьми в социальных сетях. Он позволяет определить, есть ли у пользователя возможность посетить каждого из его друзей только один раз.
4. Испытания электронных схем: алгоритм может использоваться для тестирования работоспособности электронных схем. Он помогает определить, можно ли пройти через каждое соединение схемы только один раз.

Возможности применения алгоритма Эйлера широки и разнообразны. Он может быть полезен во множестве задач, где требуется определить оптимальный путь или связь между элементами. Благодаря своей универсальности, алгоритм Эйлера является важным инструментом в различных областях науки и техники.

Алгоритм Эйлера и другие графовые алгоритмы

Один из наиболее известных графовых алгоритмов - это алгоритм Эйлера. Этот алгоритм используется для нахождения эйлерова цикла в графе. Эйлеров цикл - это цикл, который проходит через каждое ребро графа ровно один раз.

Алгоритм Эйлера основан на идее обхода графа, при котором происходит переход от одной вершины к соседней, пока есть непосещенные ребра. Этот обход совершается таким образом, чтобы обойти все ребра графа. Если в результате обхода все ребра графа были посещены и вернулись в исходную вершину, то такой обход является эйлеровым циклом.

Алгоритм Эйлера можно применять для решения различных практических задач, например, для построения оптимальных путей в сетях связи, для решения задачи коммивояжера, для построения планов раскроя материалов и других задач.

Однако алгоритм Эйлера не единственный графовый алгоритм. Существуют и другие алгоритмы, такие как алгоритмы поиска в ширину и поиска в глубину, алгоритмы для нахождения минимального остовного дерева, алгоритмы для поиска кратчайших путей и многое другое. Каждый из этих алгоритмов имеет свои особенности и применяется в своих конкретных случаях.

Рекомендации по реализации алгоритма

При реализации алгоритма Эйлера для поиска эйлерова цикла в графе, следует учесть несколько рекомендаций:

1. Необходимо представить граф в виде списка смежности или матрицы смежности. Это позволит эффективно хранить и оперировать с информацией о ребрах графа.

2. Перед тем как запустить алгоритм Эйлера, необходимо проверить, что граф является связным и все вершины имеют четную степень. Если граф не удовлетворяет этим условиям, то эйлеров цикл в нём не будет существовать.

3. Правильная реализация алгоритма Эйлера предполагает использование обхода в глубину (DFS) с рекурсией или стеком. Это позволяет обойти все ребра графа и сформировать эйлеров цикл.

4. Во время обхода графа, необходимо выполнять проверку наличия непосещенных ребер у текущей вершины. Если у текущей вершины остались непосещенные ребра, то следует продолжить обход от этой вершины.

5. При обходе графа методом DFS, необходимо использовать отметку для ребер. Это позволит избежать повторного посещения ребер и вершин.

6. В процессе обхода графа необходимо сохранять пройденные ребра в стек или другую подходящую структуру данных. Это позволит в конечном итоге сформировать эйлеров цикл.

7. После завершения обхода графа и формирования эйлерова цикла, следует проверить, что все ребра графа были посещены. Если в графе остались непосещенные ребра, то алгоритм был реализован неверно.

Соблюдение этих рекомендаций поможет реализовать алгоритм Эйлера эффективно и корректно, позволив найти эйлеров цикл в графе.