Геометрия – одна из самых увлекательных и интересных областей математики. Она изучает фигуры и их свойства, а также взаимное расположение точек, прямых и плоскостей. Один из ключевых аспектов геометрии – поиск сечения фигур. Сечение является местом пересечения двух или более фигур и может принимать различные формы, такие как отрезок, луч, окружность, эллипс и даже пустое множество.
Поиск сечения представляет собой важный этап решения задач геометрии. Чтобы успешно находить сечения, необходимо следовать определенным этапам и придерживаться некоторых полезных советов. Первым этапом является анализ задачи и определение исходных данных. Далее необходимо определить, какие фигуры сечут друг друга, и установить их связь. Важно учитывать, что фигура может иметь несколько сечений.
Вторым этапом является нахождение точек пересечения фигур. Для этого нужно решить систему уравнений или найти совместное решение уравнений, задающих фигуры. Следует помнить о том, что может быть несколько точек пересечения или сечение может быть пустым множеством. Важно уметь работать с различными видами геометрических фигур и знать их уравнения и особенности.
Определение сечения

Существуют различные типы сечений, в зависимости от объекта и задачи исследования. Некоторые из самых распространенных типов сечений включают:
| Тип сечения | Описание |
|---|---|
| Плоскостное сечение | Сечение, полученное путем пересечения плоскостью с объектом. Используется для изучения внутренней структуры и формы объекта. |
| Продольное сечение | Сечение, проведенное вдоль оси объекта. Используется для анализа изменения формы и структуры объекта вдоль его длины. |
| Перпендикулярное сечение | Сечение, проведенное перпендикулярно объекту. Используется для изучения перекрестных связей и отношений. |
Определение сечения является важным этапом в геометрии, поскольку позволяет получить информацию о структуре и характеристиках объекта. Правильный выбор типа сечения и его анализ могут привести к новым открытиям и помочь в решении различных задач и проблем.
Выбор метода поиска сечения
Поиск сечения в геометрии может быть выполнен различными методами, в зависимости от конкретной задачи. Выбор метода зависит от вида фигуры, которая требует поиска сечения, а также от доступной информации о данной фигуре.
Один из основных методов поиска сечения - метод рассечения. Этот метод заключается в том, чтобы рассечь фигуру по определенному плоскостному разрезу и исследовать геометрические свойства полученных сечений. Такой подход позволяет получить более простые и понятные фигуры, на основе которых можно провести дальнейшие исследования.
Еще одним методом поиска сечения является метод проекций. Данный метод заключается в том, чтобы проецировать фигуру на плоскость, перпендикулярную выбранному направлению сечения. Далее проводится анализ проекций и определение сечений на основе полученных данных. Этот метод часто используется при поиске сечения сложных трехмерных фигур.
В некоторых случаях возможно использование метода ассоциации. Этот метод заключается в ассоциировании фигуры с более простым объектом, знакомым геометрическим свойствам которого известны. Далее применяются известные методы поиска сечения для более простой ассоциированной фигуры, что позволяет решить исходную задачу.
При выборе метода поиска сечения необходимо учитывать конкретные условия задачи, доступные данные и требуемую точность результата. Иногда один метод может давать более точные результаты, в то время как другой метод может быть более подходящим в данной ситуации.
Важно помнить, что поиск сечения - это сложный процесс, требующий глубоких знаний геометрии и тщательного анализа. Правильный выбор метода и аккуратное выполнение всех вычислений позволят успешно решить задачу по поиску сечения, получив точные и надежные результаты.
Подготовка к поиску сечения
1. Внимательно изучите условия задачи и определите, что именно требуется найти. Это позволит вам сосредоточиться на ключевых элементах и информации, не тратя время на ненужные детали.
2. Проведите несколько эскизов или чертежей, чтобы визуализировать геометрическую ситуацию. Это поможет вам лучше понять задачу и избежать возможных ошибок при поиске сечения.
3. Используйте специальные геометрические инструменты, такие как линейка, циркуль и угольник. Они помогут вам провести необходимые линии и углы, что может значительно упростить поиск сечения.
4. Обратите внимание на особенности фигур, с которыми вы работаете. Изучите различные типы сечений и их свойства. Это поможет вам выбрать правильный подход к поиску и решению задачи.
5. Проработайте несколько примеров сечений, чтобы наработать навык и уверенность в своих знаниях. Попробуйте решить задачи разной сложности и постепенно усложняйте свои упражнения.
Следуя этим советам, вы сможете грамотно подготовиться к поиску сечения в геометрии и успешно решить задачу. Помните, что практика и терпение играют важную роль в достижении успеха в этой области.
Процесс поиска сечения
1. Определите фигуры, с которыми вы работаете. Изучите их характеристики и свойства. Определите, какие фигуры рассматриваются в задаче.
2. Определите, какие данные даны и какие данные необходимо найти для решения задачи. Это может быть длина, площадь, периметр и так далее.
3. Изучите способы нахождения сечения заданных фигур. Некоторые общие методы включают использование геометрических теорем, формул и свойств фигур.
4. Примените соответствующий метод для решения задачи. Если вы затрудняетесь, найдите примеры решения подобных задач, чтобы лучше понять процесс.
5. Проверьте свое решение. Убедитесь, что результаты соответствуют данным и правилам геометрии.
Важно: Для более сложных задач может потребоваться комбинирование разных методов и использование дополнительных свойств фигур.
Проявите терпение и упорство. Поиск сечения может быть сложным процессом, но с практикой вы станете лучше в решении геометрических задач.
Примеры сечений в геометрии
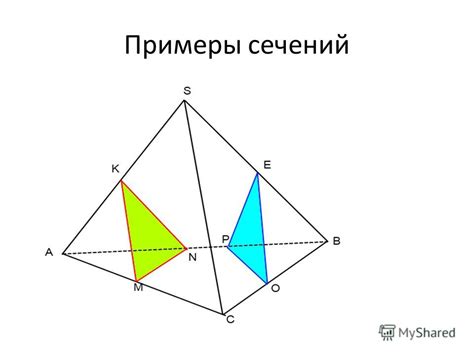
- Параллельные сечения: две параллельные плоскости, которые пересекают фигуру, делят ее на параллельные секции, такие как параллелограммы или прямоугольники.
- Перпендикулярные сечения: две перпендикулярные плоскости, которые пересекают фигуру под прямым углом, создают перпендикулярные секции, например, куб или прямоугольный параллелепипед.
- Диагональные сечения: линия или плоскость, которая проходит сквозь фигуру и не параллельна ее сторонам. Например, диагональное сечение через прямоугольник или треугольник.
- Случайные сечения: это любые другие сечения, которые могут быть проведены через фигуру без определенной геометрической связи. Например, ломаная линия, которая пересекает окружность в разных точках.
Знание различных примеров сечений в геометрии помогает в понимании свойств и особенностей фигур, а также в решении задач, связанных с их пространственным разделением или пересечением.