Котангенс угла α – одна из основных тригонометрических функций, которая широко используется при решении задач в математике и ее приложениях. Котангенс обратно пропорционален тангенсу угла α и является важным инструментом для анализа и вычислений в треугольниках.

Формула котангенса угла α определяется как отношение прилежащего катета к противолежащему катету для прямоугольного треугольника, где угол α примыкает к прилежащему катету. Формула записывается следующим образом:

cot(α) = cos(α) / sin(α)

где cos(α) – косинус угла α, sin(α) – синус угла α.

Котангенс угла α может также быть вычислен через тангенс угла α по формуле:

cot(α) = 1 / tan(α)

В математике формула котангенса угла α применяется для нахождения неизвестных сторон и углов треугольника, а также для решения задач по геометрии и тригонометрии. Для использования формулы необходимо знать значения косинуса и синуса угла α или значение тангенса угла α.

Формула котангенса угла α в математике

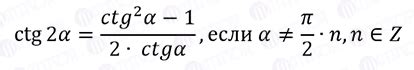
Формула котангенса угла α выглядит следующим образом:

cot(α) = 1 / tan(α) = cos(α) / sin(α)

где:

• cot(α) - котангенс угла α;
• tan(α) - тангенс угла α;
• cos(α) - косинус угла α;
• sin(α) - синус угла α.

Пример использования формулы котангенса:

Дан прямоугольный треугольник ABC, угол ACB составляет 30°. Найти котангенс угла ACB:

cot(30°) = 1 / tan(30°) = 1 / (sqrt(3) / 3) ≈ 1.732

Таким образом, котангенс угла ACB равен примерно 1.732.

Правила

Котангенс угла a определяется как обратная величина тангенса данного угла. Его можно выразить через отношение сторон прямоугольного треугольника.

Для нахождения котангенса угла a нужно использовать следующую формулу: cot(a) = b/a, где b - длина катета, противолежащего углу a, а a - длина катета, прилегающего к углу a.

Стоит отметить, что котангенс угла a подразумевает, что сравнивается отношение сторон прямоугольного треугольника, и поэтому значение котангенса всегда положительно.

Например, находим котангенс угла a, если катет b = 3 и катет a = 4:

cot(a) = 3/4 = 0.75

Таким образом, котангенс угла a, при заданных значениях катетов, равен 0.75.

Примеры

Давайте рассмотрим несколько примеров использования формулы котангенса.

• Пример 1: Рассчитаем котангенс угла α, если известно, что синус угла α равен 0.5.
  Решение: Известно, что котангенс угла α равен обратному значению тангенса угла α. Так как тангенс угла α можно найти, используя формулу тангенса теоремы синусов, получаем: тангенс α = синус α / корень(1 - синус^2(α)). Подставляем известные значения и получаем: тангенс α = 0.5 / корень(1 - 0.5^2) = 0.5 / корень(1 - 0.25) = 0.5 / корень(0.75) = 0.5 / 0.866 ≈ 0.577. Таким образом, котангенс угла α ≈ 1 / 0.577 ≈ 1.732.
• Пример 2: Вычислим значение котангенса угла β, если тангенс угла β равен -2.
  Решение: Так как котангенс угла β равен обратному значению тангенса угла β, найдем тангенс α по известному значению: котангенс β = 1 / тангенс β = 1 / (-2) = -0.5. Таким образом, котангенс угла β равен -0.5.
• Пример 3: Пусть у нас есть треугольник ABC, где угол A равен 30 градусов, а угол B равен 60 градусов. Найдем котангенс угла C.
  Решение: Известно, что сумма углов треугольника равна 180 градусов, поэтому угол C равен 180 - (30 + 60) = 90 градусов. Так как котангенс угла C равен обратному значению тангенса угла C, можно воспользоваться формулой тангенса теоремы синусов: тангенс C = синус C / корень(1 - синус^2(C)). Подставив известные значения, получим: тангенс C = синус 90 градусов / корень(1 - синус^2(90 градусов)) = 1 / корень(1 - 1^2) = 1 / корень(0) = 1 / 0, что не имеет смысла. Поэтому котангенс угла C не существует в данном случае.

Это лишь некоторые примеры использования формулы котангенса. Надеюсь, они помогут вам лучше понять и применять данную математическую концепцию.