Синус - один из основных тригонометрических показателей, который используется в геометрии, физике, астрономии и других науках. Он определяет отношение длины противоположной стороны прямоугольного треугольника к гипотенузе. Нахождение синуса требует знания формулы, которая позволяет его вычислить по известным сторонам треугольника. В данном подробном руководстве мы рассмотрим эту формулу.
Для вычисления синуса прямоугольного треугольника необходимо знать длины двух его сторон: противоположной и гипотенузы. Формула для нахождения синуса такого треугольника выглядит следующим образом:
sin A = противоположная сторона / гипотенуза
Здесь A - угол, противоположный стороне, длина которой известна. Например, если известны длины сторон A и C, а угол B противоположен стороне C, то синус этого угла можно вычислить, подставив известные значения в формулу. В результате получим значение синуса, которое поможет нам решать задачи, связанные с треугольниками.
Зная формулу нахождения синуса в прямоугольном треугольнике, вы можете решать разнообразные задачи, которые представляются вам в геометрии или других научных областях. Уверенное владение этой формулой позволит вам решать сложные задачи и получать точные результаты.
Формула нахождения синуса

| sin(A) = | a |
| c |
где A - это угол между противолежащим катетом и гипотенузой.
Также, синус можно представить как отношение ординаты (y) к радиусу (r) точки на единичной окружности с углом α:
| sin(α) = | y |
| r |
Где α - это угол между радиусом точки на окружности и положительным направлением оси x.
Формула нахождения синуса позволяет легко определить значение синуса угла, используя известные длины сторон прямоугольного треугольника или координаты точек на единичной окружности. Это важный инструмент в математике и естественных науках.
Определение синуса
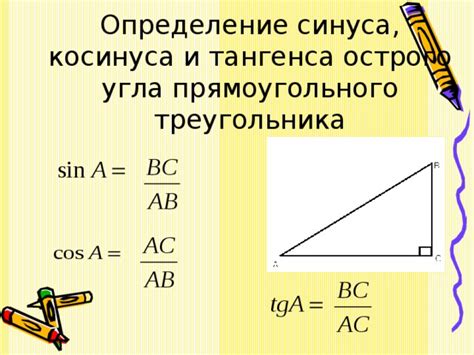
Таким образом, синус угла А в прямоугольном треугольнике вычисляется по формуле:
sin(A) = a / c, где a – длина противоположного катета, c – длина гипотенузы.
Синус угла может принимать значения от -1 до 1 включительно. Отрицательные значения соответствуют углам, для которых противоположный катет а лежит в отрицательной полуплоскости координат.
Вычисление синуса угла является одной из основных операций в тригонометрии и находит широкое применение в различных областях науки и техники.
Основные свойства синуса
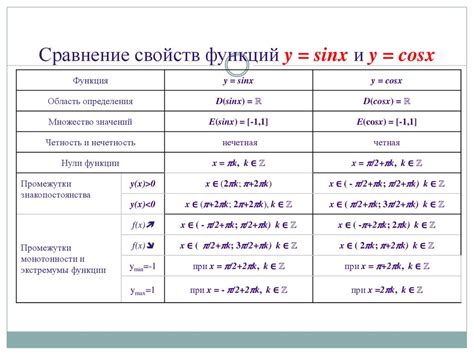
Главные свойства синуса:
- Значение синуса находится в пределах от -1 до 1: |sin α| ≤ 1.
- Синус острого угла α равен синусу его дополнения: sin α = sin (π/2 - α).
- Обратные версии синуса: для данного значения sin α можно найти угол α, обозначаемый как α = arcsin x или α = sin-1 x. Здесь x – значение синуса.
- Синусная функция периодична: sin (α + 2πk) = sin α, где k – целое число.
- Синус – нечётная функция: sin (-α) = -sin α.
- Синус является гладкой и непрерывной функцией на всей числовой оси.
Эти свойства синуса играют важную роль при решении задач и применении тригонометрии в различных областях науки и техники.
Прямоугольный треугольник

Основная формула, используемая для расчета сторон прямоугольного треугольника, называется теоремой Пифагора. Согласно этой теореме, квадрат длины гипотенузы (самой длинной стороны, противоположной прямому углу) равен сумме квадратов длин катетов (других двух сторон) треугольника. Формула записывается следующим образом:
c^2 = a^2 + b^2
где c - длина гипотенузы, a и b - длины катетов.
Также, для нахождения значений углов прямоугольного треугольника, используется тригонометрический круг. В частности, для нахождения синуса угла используется отношение противолежащего катета к гипотенузе. Формула выглядит следующим образом:
sin(A) = a / c
где A - угол, а - противолежащий катет, c - гипотенуза.
Эти формулы могут быть использованы для решения различных задач, связанных с прямоугольными треугольниками, таких как нахождение длин сторон, углов или высоты треугольника.
Катеты и гипотенуза
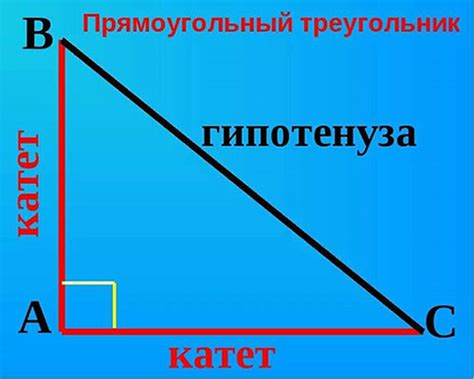
Катеты и гипотенуза связаны друг с другом формулой Пифагора:
a2 + b2 = c2
где a и b - длины катетов, а c - длина гипотенузы.
Формула Пифагора позволяет находить длину одной из сторон прямоугольного треугольника, если известны длины остальных двух сторон. Также она используется для нахождения углов треугольника, если известны длины его сторон.
Таким образом, знание длин катетов и гипотенузы, а также умение применять формулу Пифагора, являются важными навыками при работе с прямоугольными треугольниками и вычислении их свойств.
Пример:
Пусть катеты прямоугольного треугольника равны 3 см и 4 см. Чтобы найти длину гипотенузы, мы можем воспользоваться формулой Пифагора:
32 + 42 = c2
9 + 16 = c2
25 = c2
c = 5 см.
Таким образом, длина гипотенузы этого треугольника равна 5 см.
Формула нахождения синуса в прямоугольном треугольнике

Синус угла в прямоугольном треугольнике можно найти, используя отношение длины противоположенного катета к гипотенузе:
sin(α) = a / c
Где:
- sin(α) - синус угла α;
- a - длина противоположенного катета;
- c - длина гипотенузы.
Для примера, рассмотрим прямоугольный треугольник со сторонами a = 3 и c = 5. Чтобы найти синус угла α, мы используем формулу:
sin(α) = 3 / 5
Таким образом, синус угла α равен 0.6.
Формула нахождения синуса в прямоугольном треугольнике позволяет нам определить отношение длин сторон и углов, что является важным для решения геометрических задач и применения их в реальной жизни.
Подробное руководство

Нахождение синуса в прямоугольном треугольнике может быть проще, чем кажется. Для этого нужно знать длины двух сторон треугольника: гипотенузы и прилежащего к углу, для которого мы хотим найти синус.
Сначала нужно определить, какая сторона является гипотенузой. Гипотенуза – это самая длинная сторона треугольника, напротив прямого угла. Обозначим ее как c.
Затем нужно найти длину стороны, прилежащей к углу, для которого мы хотим найти синус. Обозначим ее как a. При этом необходимо обратить внимание на то, что сторона, примыкающая к углу и являющаяся гипотенузой, не может быть стороной, прилежащей к углу, для которого мы ищем синус.
Теперь мы готовы вычислить синус угла. Формула для вычисления синуса прямоугольного треугольника выглядит следующим образом:
sin(A) = a / c
Где A - значение угла, для которого мы вычисляем синус, a - длина стороны прилежащей к этому углу и c - длина гипотенузы.
Теперь остается только подставить значения сторон в формулу и выполнить вычисление. Полученное значение будет являться синусом заданного угла в прямоугольном треугольнике.