Формула полной вероятности - это один из фундаментальных инструментов теории вероятностей, который позволяет нам находить вероятности событий, основываясь на информации о других связанных событиях. Эта формула является основой для многих статистических методов и анализа данных.
Основная идея формулы полной вероятности заключается в разбиении пространства элементарных исходов на непересекающиеся события и вычислении вероятности каждого из них. Затем эти вероятности событий умножаются на вероятность каждого независимого события, произошедшего внутри этих групп.
Применение формулы полной вероятности возможно в различных задачах, включая статистику, экономику, биологию и другие области науки. Она помогает нам оценивать вероятности различных событий на основе имеющихся данных и предположений.
Формула Байеса - это еще один инструмент теории вероятностей, который позволяет нам обновлять вероятности событий на основе новой информации. Эта формула получила свое название по имени английского математика и статистика Томаса Байеса, который разработал ее в XVIII веке.
Основной принцип работы формулы Байеса заключается в использовании априорных вероятностей - вероятностей, которые у нас уже есть перед получением новой информации, и формировании апостериорных вероятностей - вероятностей, которые мы получаем после учета новой информации.
Формула Байеса является основой для байесовских методов статистического анализа, машинного обучения и искусственного интеллекта. Она широко применяется в различных областях, включая медицину, финансы, технологии и многие другие.
Формула полной вероятности и формула Байеса

Формула полной вероятности позволяет вычислить вероятность наступления события A, основываясь на наборе условий (или событий), известных как вариации события A. Эта формула используется в ситуациях, когда событие A может происходить на основе различных условий или исходов.
Формула полной вероятности выглядит следующим образом:
P(A) = P(A|B1) * P(B1) + P(A|B2) * P(B2) + ... + P(A|Bn) * P(Bn)
где P(A) - вероятность наступления события A, P(A|Bi) - условная вероятность наступления события A при условии Bi, P(Bi) - вероятность наступления условия Bi.
Формула Байеса позволяет обратиться к условным вероятностям в противоположную сторону, вычисляя вероятности наступления условий при наступлении события A.
Формула Байеса имеет следующий вид:
P(B|A) = (P(A|B) * P(B)) / P(A)
где P(B|A) - условная вероятность наступления условия B при наступлении события A, P(A|B) - условная вероятность наступления события A при условии B, P(B) - вероятность наступления условия B, P(A) - вероятность наступления события A.
Использование формул полной вероятности и Байеса позволяет решать широкий спектр задач, связанных с оценкой вероятностей, на основе доступных данных и условий.
Принципы работы формулы полной вероятности

1. Разделение событий
Формула полной вероятности предполагает, что исследуемое событие может произойти только при наступлении одного из нескольких взаимоисключающих событий. Отдельные события разделяются на отдельные части и анализируются независимо друг от друга.
2. Определение вероятностей условных событий
Формула полной вероятности основана на вычислении вероятностей условных событий. Условная вероятность определяется как вероятность наступления события B при условии, что произошло событие A. Эти вероятности представляют собой статистические данные, полученные из исходного набора данных.
3. Умножение вероятностей условных событий
Для каждого условного события вычисляется вероятность исследуемого события, учитывая вероятности всех возможных условий происхождения события. Для этого используется принцип умножения вероятностей. Этот шаг позволяет учесть все возможные комбинации условий и вычислить вероятность наступления исследуемого события.
4. Суммирование вероятностей всех событий
В заключительном шаге все вычисленные вероятности условных событий суммируются, чтобы получить полную вероятность наступления исследуемого события. Значение полной вероятности представляет собой сумму всех частных вероятностей, полученных на предыдущих шагах анализа.
Таким образом, формула полной вероятности является мощным инструментом для анализа вероятностей и позволяет учесть все возможные сценарии наступления событий. Ее применение основано на вычислении условных вероятностей и суммировании результатов, что позволяет получить точные и надежные результаты анализа вероятностей событий.
Принципы работы формулы Байеса

- Априорные вероятности: формула Байеса использует априорные (начальные) вероятности событий, которые могут быть известны заранее или определены на основе предыдущих данных. Эти вероятности представляют собой начальные предположения о вероятностях событий до получения новой информации.
- Вероятность данных: формула Байеса учитывает вероятность получения конкретных данных при наступлении определенного события. Эта вероятность может быть измерена или определена на основе статистических данных и экспертных оценок.
- Обновление вероятности: основной принцип формулы Байеса заключается в обновлении априорных вероятностей событий на основе новой информации. Формула позволяет учесть, какая информация была получена, и пересчитать вероятности событий с учетом этой информации.
- Использование постериорных вероятностей: результатом применения формулы Байеса являются постериорные (последующие) вероятности событий. Они представляют собой обновленные вероятности, которые учитывают новую информацию и позволяют принимать во внимание эти обновленные данные при принятии решений.
Принципы работы формулы Байеса позволяют эффективно использовать вероятностный анализ и статистику для принятия решений на основе доступной информации. Формула Байеса находит широкое применение в различных областях, таких как медицина, финансы, машинное обучение и другие, где важно учитывать новую информацию и обновлять предварительные предположения о вероятностях событий.
Применение формулы полной вероятности

Одним из простых примеров применения формулы полной вероятности является случай подбрасывания игральной кости. Пусть у нас есть шесть возможных исходов, каждый из которых равновероятен. Мы хотим вычислить вероятность выпадения определенного числа очков, например, четного числа. Для этого мы можем разделить событие выпадения четного числа на несколько исходов: выпадение двух, четырех или шести очков. Затем, используя вероятности каждого из этих исходов, мы можем вычислить общую вероятность выпадения четного числа, применяя формулу полной вероятности.
Применение формулы полной вероятности также может быть полезно при анализе случайных событий в реальной жизни. Например, если мы хотим вычислить вероятность того, что мы опоздаем на работу, мы можем разделить это событие на несколько исходов: пробка на дороге, задержка общественного транспорта и т.д. Затем, используя вероятности каждого из этих исходов, мы можем вычислить общую вероятность опоздания, применяя формулу полной вероятности.
Таким образом, формула полной вероятности является мощным инструментом для анализа случайных событий. Она позволяет вычислить вероятности в различных ситуациях, учитывая вероятности различных исходов. Применение этой формулы может помочь в принятии решений и понимании вероятностных свойств случайных событий.
Применение формулы Байеса
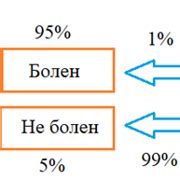
Основная идея формулы Байеса заключается в том, что мы можем обновить наши представления о вероятности события, учитывая новую информацию. Он предоставляет нам инструмент для пересмотра наших суждений и уточнения наших прогнозов.
Применение формулы Байеса может быть полезно в различных ситуациях. Допустим, у нас есть медицинский тест на определенное заболевание. Формула Байеса позволяет нам рассчитать вероятность наличия заболевания у пациента, исходя из результатов теста и информации о предыдущей вероятности заболевания в общей популяции.
Еще одним примером применения формулы Байеса является распознавание спам-сообщений. Зная вероятности встречи отдельных слов или фраз в спам-сообщениях и в "чистых" сообщениях, мы можем использовать формулу Байеса для расчета вероятности того, что конкретное сообщение является спамом или нет.
Кроме того, формула Байеса применяется в байесовской статистике, где она позволяет учитывать априорные вероятности при проведении статистических анализов и оценке параметров.
Важно отметить, что формула Байеса имеет свои предположения, которые могут быть нарушены в реальных ситуациях. Однако, с правильным использованием и оценкой параметров, она может быть мощным инструментом для принятия решений и выяснения зависимостей между событиями.