Квадратное уравнение - это уравнение вида ax2 + bx + c = 0, где a, b и c - это коэффициенты, причем a не равно нулю. Одно из наиболее важных понятий в решении квадратных уравнений - это дискриминант.
Дискриминант (обозначается как D) - это выражение под знаком корня в формуле для нахождения корней квадратного уравнения. Если дискриминант больше нуля, то уравнение имеет два различных корня. Если дискриминант равен нулю, то уравнение имеет один корень. И, наконец, если дискриминант меньше нуля, то уравнение не имеет корней в области вещественных чисел.
Когда дискриминант равен нулю, существует специальная формула, которая позволяет найти этот корень. Формула выглядит следующим образом:
x = -b / (2a)
Здесь x - это корень квадратного уравнения, а a и b - коэффициенты из исходного уравнения. Она основывается на том факте, что при D = 0, выражение под знаком корня равно нулю, а значит, корень будет простым числом.
Используя данную формулу, можно легко и быстро найти корень квадратного уравнения, если известно, что дискриминант равен нулю. Это может быть полезно при решении математических задач, а также в различных областях науки и инженерии.
Расчет дискриминанта и его значение
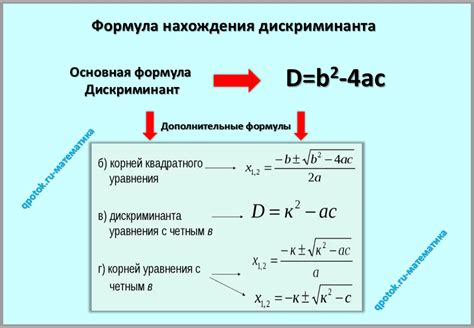
D = b2 - 4ac
где a, b и c - коэффициенты квадратного уравнения ax2 + bx + c = 0.
Значение дискриминанта может принимать три различных варианта:
- Если дискриминант больше нуля, то у квадратного уравнения есть два различных действительных корня.
- Если дискриминант равен нулю, то у квадратного уравнения есть один действительный корень, который называется кратным.
- Если дискриминант меньше нуля, то у квадратного уравнения нет действительных корней, а имеются только комплексные.
Таким образом, расчет и значение дискриминанта позволяют определить характер решений квадратного уравнения и понять, сколько действительных корней оно имеет.
Формула для расчета корня дискриминанта при D = 0

Формула для расчета корня дискриминанта при D = 0 выглядит следующим образом:
x = -b / (2a)
В этой формуле переменные a, b и c соответствуют коэффициентам квадратного уравнения ax^2 + bx + c = 0.
Когда дискриминант равен нулю, это означает, что подкоренное выражение D = b^2 - 4ac равно нулю. Таким образом, корень дискриминанта равен нулю и квадратное уравнение имеет один действительный корень, который находится по формуле выше.
Уравнение с одним корнем может иметь разные геометрические интерпретации. Например, при графическом представлении квадратного уравнения, оно будет представлять собой параболу, касающуюся оси x в одной точке. Также можно интерпретировать такое уравнение как ситуацию, когда прямая, заданная этим уравнением, пересекает ось x только в одной точке.
Использование формулы для расчета корня дискриминанта при D = 0 позволяет легко и быстро определить, сколько корней имеет квадратное уравнение и вычислить значение корня в случае, когда дискриминант равен нулю.