Тригонометрия – одна из основных разделов математики, и формула тангенса является одной из важнейших формул этой науки. Тангенс – это отношение длины противолежащего катета к длине прилежащего катета в прямоугольном треугольнике. Формула тангенса позволяет вычислить значение угла по отношению к двум сторонам треугольника. Она является одной из базовых математических формул и находит широкое применение в различных областях науки и техники.
Формула тангенса представляет собой простое соотношение между противолежащим катетом (a) и прилежащим катетом (b). Иначе говоря, тангенс угла можно найти, разделив длину противолежащего катета на длину прилежащего катета:
tg(α) = a / b
Формула тангенса позволяет находить значения углов при известных длинах катетов. Пользуясь этой формулой, можно решать задачи на нахождение неизвестных углов в прямоугольном треугольнике. Также тангенс широко используется в тригонометрических функциях и формулах, например, при вычислении значения синуса и косинуса.
Формула тангенса имеет множество приложений в различных областях. Она применяется в геодезии и навигации для определения высот точек, углов наклона и азимута направлений. Также формула тангенса играет важную роль в физике и инженерных расчетах. Например, при проектировании строительных конструкций и прочности материалов. Знание формулы тангенса и ее применение существенно расширяет возможности в решении различных задач и позволяет успешно применять математические модели в практической деятельности.
Что такое тангенс в тригонометрии?
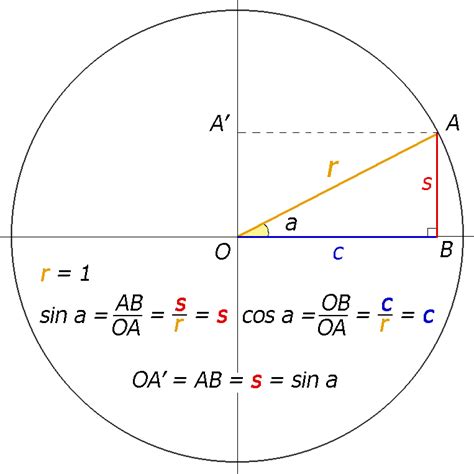
Математически тангенс выражается следующей формулой:
- Тангенс угла α = противоположная сторона / прилежащая сторона
- Тангенс α = a / b
Здесь α - угол, а a и b - стороны прямоугольного треугольника, смежные с углом α.
Тангенс может принимать любое числовое значение, и его график является периодической функцией. Значение тангенса может быть отрицательным, положительным или нулевым в зависимости от угла, на который мы смотрим.
Тангенс широко используется в различных областях науки и инженерии. Его часто применяют в геодезии, физике, радиотехнике, компьютерной графике и других дисциплинах. Тангенс позволяет решать задачи, связанные с геометрией, тригонометрией, а также моделирование и анализ различных явлений.
Понятие и особенности

Формула тангенса может быть использована для нахождения как неизвестных сторон треугольника, так и неизвестных углов. Для нахождения значения угла по известным сторонам можно использовать обратную формулу тангенса.
Применение формулы тангенса широко распространено в различных областях, включая физику, инженерию, геодезию и компьютерную графику. Например, она может использоваться для расчета углов наклона при строительстве или для моделирования трехмерных объектов.
Важно помнить, что формула тангенса применима только к прямоугольным треугольникам и может быть использована только для вычисления отношений между сторонами и углами в таких треугольниках.
Как найти значение тангенса в тригонометрии?
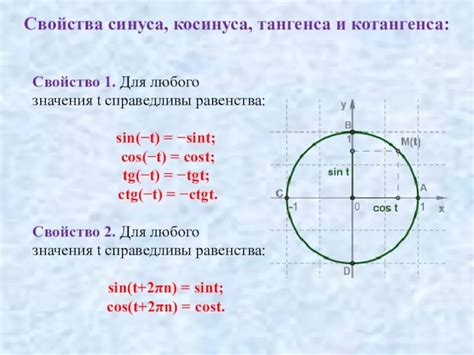
Для нахождения значения тангенса используется формула:
tan α = противолежащий катет / прилежащий катет
Здесь α – это угол между горизонтальной осью и линией, соединяющей начало координат и точку на круге единичного радиуса.
Пример:
Пусть угол α = 45°. Для нахождения значения тангенса пригодится знание, что в прямоугольном треугольнике со сторонами, равными 1, гипотенуза равна √2. Тогда:
tan α = 1 / 1 = 1.
Полученное значение тангенса будет 1.
Таким образом, для нахождения значения тангенса необходимо знание значений противолежащего и прилежащего катетов прямоугольного треугольника, а также применение соответствующей формулы.
Формула нахождения

Формула тангенса определяется как отношение противоположного катета к прилежащему катету прямоугольного треугольника.
Формула тангенса выглядит следующим образом:
- для прямоугольного треугольника: tg(α) = a/b, где α - угол, a - противоположный катет, b - прилежащий катет;
- для остроугольного и тупоугольного треугольника: tg(α) = a/b, где α - угол, a - противоположная сторона, b - прилежащая сторона.
Формула тангенса широко применяется в геометрии, физике и других науках для решения задач, связанных с треугольниками и углами. Она позволяет вычислить значение тангенса угла по известным сторонам или катетам треугольника и вычислить угол по известному значению тангенса.
Практическое применение тангенса в математике и физике

1. Геометрия:
Тангенс можно использовать для нахождения углов в треугольниках. Например, если известны две стороны треугольника и угол между ними, то тангенс этого угла можно вычислить с помощью формулы тангенса. Это позволяет нам определить все остальные углы треугольника.
2. Физика:
В физике тангенс применяется для решения задач, связанных с движением и силами. Например, если нам известен угол наклона плоскости и сила, действующая на тело, можно вычислить проекцию этой силы по оси плоскости с помощью тангенса. Это помогает нам анализировать движение объектов на наклонной плоскости.
3. Инженерия:
Тангенс также применяется в различных инженерных расчетах, связанных с определением углов. Например, в строительстве можно использовать тангенс для нахождения высоты строения, зная угол наклона некоторого измерительного прибора и расстояние до строения.
Примеры применения

Формула тангенса в тригонометрии широко применяется в различных областях, включая геометрию, физику, инженерию и компьютерную графику.
- Геометрия: Формула тангенса позволяет находить значения тангенса угла в прямоугольном треугольнике, что позволяет определить соотношение сторон и углов треугольника.
- Физика: Тангенс угла часто используется для анализа движения, векторов сил и моментов, а также для описания характеристик колебаний и звука.
- Инженерия: В области инженерии формула тангенса широко используется для расчетов и проектирования механизмов, а также для моделирования и анализа электрических и электронных цепей.
- Компьютерная графика: Формула тангенса часто применяется для создания реалистичных трехмерных моделей, текстурирования объектов и создания эффектов освещения.
Это лишь некоторые примеры применения формулы тангенса в различных областях. Высокая точность и широкое использование этой формулы делают ее важным инструментом в научных и технических исследованиях.