Считается, что синус - это одна из основных тригонометрических функций, которая широко используется в математике, физике, инженерии и других науках. Она помогает решать различные задачи, связанные с колебаниями, волнами, периодическими процессами и много другим. Зная значение угла, мы можем вычислить его синус и использовать полученный результат в дальнейших расчетах.
Формула для вычисления синуса числа основывается на соотношении между сторонами прямоугольного треугольника. Синус угла равен отношению противолежащего катета к гипотенузе треугольника. Основываясь на этом, можно вывести универсальную формулу, которая применима для всех значений угла. Важно отметить, что угол измеряется в радианах, а формула актуальна только для прямоугольного треугольника.
Для вычисления синуса числа можно воспользоваться различными методами и алгоритмами. Один из самых распространенных способов - использование разложения в ряд Тейлора, которое позволяет приближенно вычислить синус для небольших значений угла. Еще одним методом является использование таблицы значений синуса. Этот метод достаточно прост для использования, но требует большого объема данных и не является точным для всех значений угла.
Зачем нужна формула вычисления синуса?

Синус является основной тригонометрической функцией и используется для описания различных физических явлений, например, колебаний, волн и периодических процессов. Применение формулы вычисления синуса позволяет упростить и ускорить решение задач, связанных с этими явлениями.
Формула вычисления синуса может быть использована для нахождения неизвестных углов в треугольниках или решения задач геометрии, связанных с тригонометрическими функциями.
Кроме того, синус является основой для других тригонометрических функций, таких как косинус и тангенс. Формула вычисления синуса позволяет находить значения этих функций и использовать их для решения более сложных задач, например, вычисления длины сторон треугольника или нахождения противоположного угла.
Таким образом, формула вычисления синуса является важным инструментом для решения различных математических и инженерных задач, а также широко применяется в научных исследованиях и практической деятельности.
Переведем задачу в математическую формулировку
Чтобы вычислить синус числа, нужно использовать математическую формулу, которая основывается на тригонометрии. Для этого необходимо знать значения угла и его измерение.
Формула вычисления синуса числа выглядит следующим образом:
sin(x) = opposite / hypotenuse
Где:
- sin(x) - синус угла x;
- opposite - длина противоположной стороны;
- hypotenuse - длина гипотенузы.
Данная формула позволяет вычислить синус угла по длинам сторон прямоугольного треугольника, в котором данный угол является одним из острых углов.
Примечание: Значения синуса могут находиться в пределах от -1 до 1, в зависимости от угла и его измерения (радианы или градусы).
Принцип работы формулы вычисления синуса

Принцип работы формулы вычисления синуса основывается на том, что синус угла можно выразить через отношение сторон прямоугольного треугольника или через бесконечный ряд тригонометрических функций.
Наиболее распространенная формула вычисления синуса основана на бесконечном ряде тригонометрических функций, называемом рядом Тейлора или рядом Маклорена. Этот ряд представляет собой сумму бесконечного числа слагаемых, каждое из которых зависит от степени угла и коэффициентов ряда.
Для вычисления синуса числа вам потребуется знать значения угла в радианах и использовать формулу, которая выражена через бесконечный ряд тригонометрических функций.
Преимуществом формулы вычисления синуса по ряду Тейлора является ее точность, поскольку ряд учитывает все слагаемые и аппроксимирует значение синуса с большой точностью. Однако, для больших значений угла сходимость ряда может быть недостаточной, и в этом случае необходимо использовать другие методы вычисления синуса.
Использование формулы вычисления синуса в программировании

В программировании существует несколько способов вычисления синуса числа. Один из наиболее распространенных методов - использование ряда Тейлора. Ряд Тейлора представляет собой разложение функции в бесконечную сумму. Для вычисления синуса числа используется следующая формула:
sin(x) = x - (x^3/3!) + (x^5/5!) - (x^7/7!) + ...
Где x - исходное число, а ! обозначает факториал.
Для программной реализации формулы вычисления синуса важно учесть несколько вещей:
- За точность вычислений отвечает количество итераций ряда Тейлора. Чем больше итераций, тем выше точность, но и больше требуется вычислительных ресурсов.
- Использование библиотеки математических функций может быть более эффективным способом для вычисления синуса числа.
- Углы могут быть представлены в различных форматах: радианы, градусы или в обратных функциях (арксинус).
Некоторые языки программирования уже имеют встроенные функции для вычисления синуса чисала, такие как Math.sin() в JavaScript, Math.sin() в Python или sin() в C++. Однако, понимание и использование формулы вычисления синуса может быть полезным при разработке собственных алгоритмов или при работе с языками программирования, которые не имеют встроенных функций для синуса.
Важно помнить, что любые вычисления, связанные с тригонометрией, могут иметь неточности из-за ограничений представления чисел в компьютерах. Поэтому при разработке программ, где точность вычислений имеет значение, рекомендуется обратиться к специализированным библиотекам или методам, которые обеспечивают более точные результаты.
Результаты точного и приближенного вычисления синуса
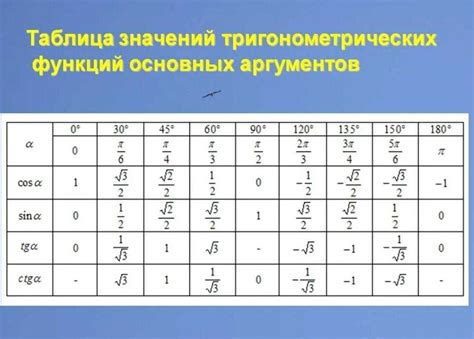
Точное вычисление синуса основывается на математической формуле, известной как ряд Тейлора. Этот ряд позволяет представить синус как бесконечную сумму степеней числа. Точное вычисление синуса позволяет получить результат с высокой степенью точности, однако может быть сложным и затратным с вычислительной точки зрения.
Приближенное вычисление синуса, в свою очередь, основывается на различных аппроксимационных методах, таких как ряды Маклорена или методы интерполяции. Эти методы позволяют получить приближенное значение синуса с некоторой погрешностью, однако они обычно более быстры и проще в вычислительном отношении.
При сравнении результатов точного и приближенного вычисления синуса, важно учитывать степень точности, которая требуется в конкретной ситуации. Для большинства задач, требующих вычисления синуса, приближенное значение с погрешностью в несколько процентов может быть достаточным, в то время как для более точных расчетов может потребоваться использование точного вычисления.
Основные принципы формулы вычисления синуса

Формула вычисления синуса числа основана на геометрических свойствах треугольника. Синус угла представляет отношение противоположного катета к гипотенузе в прямоугольном треугольнике.
Существует несколько способов вычисления синуса числа, включая ряд Тейлора, ряд Фурье и другие математические формулы. Однако наиболее распространенным и практичным методом является использование разложения синуса в ряд Маклорена.
Ряд Маклорена – это представление функции в виде бесконечной суммы ее производных в точке, называемой центральной точкой разложения. В случае с синусом, разложение основывается на том, что функция и ее производные имеют определенные значения в точке 0. Таким образом, синус может быть представлен в виде суммы бесконечно убывающих слагаемых.
Формула вычисления синуса числа по ряду Маклорена выглядит следующим образом:
sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...
Где x – значение угла в радианах, и знаки перед степенями x чередуются. Факториалы в знаменателях гарантируют убывание слагаемых с каждым новым членом ряда.
Формула вычисления синуса позволяет точно и быстро определить значение синуса для любого угла, используя лишь арифметические операции: сложение, вычитание, умножение и деление.
Ограничения при использовании формулы вычисления синуса

При использовании формулы вычисления синуса числа необходимо учитывать некоторые ограничения, которые могут повлиять на точность и результат вычислений. Вот основные ограничения, которые нужно учитывать:
| Ограничение | Описание |
|---|---|
| Угловая мера | Формула вычисления синуса предназначена для использования с углами, измеряемыми в радианах. При использовании углов в других мерах (например, градусах) результат может быть неточным. |
| Периодичность | Синус функции имеет периодическую природу. Это значит, что при использовании формулы вычисления синуса для больших значений углов (например, значений, близких к числу pi), результат может отклоняться от ожидаемого. |
| Округление и погрешность | При округлении чисел при вычислении синуса может возникнуть погрешность, особенно при большом количестве операций. Это может привести к накоплению ошибок и искажению результатов. |
| Диапазон значений | Формула вычисления синуса может быть ограничена диапазоном значений, для которых она является точной. При выходе за этот диапазон результаты могут быть неточными или непредсказуемыми. |
| Аппроксимация | Большинство формул вычисления синуса основаны на аппроксимации функции с использованием ряда или других методов. Это значит, что результаты могут быть приближенными и иметь погрешность. |
Учитывая эти ограничения, важно быть внимательным и аккуратным при использовании формулы вычисления синуса числа. Необходимо учитывать контекст и требования задачи, а также использовать более точные методы вычисления, если точность является критическим фактором.
Примеры применения формулы вычисления синуса
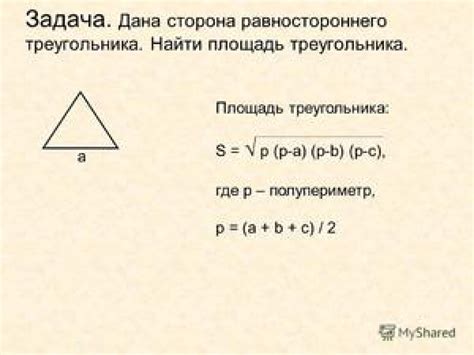
Например, формула синуса может быть использована в физике при расчете колебаний и волновых процессов. С ее помощью можно определить амплитуду, частоту и фазу колебаний, а также предсказать будущие значения величин.
В геометрии формула вычисления синуса используется для нахождения отношения длин сторон и углов треугольника. Это позволяет решать разнообразные задачи, связанные с определением размеров и форм объектов.
Еще одним примером применения формулы синуса является тригонометрическая интерполяция. С ее помощью можно приближенно вычислить значения функции синуса для промежуточных значений аргумента.
И, конечно, формула вычисления синуса числа находит применение в программировании. Она используется для создания алгоритмов, требующих работы с тригонометрическими функциями, например, при разработке компьютерных игр или программ для трехмерной графики.
Важно отметить, что для вычисления синуса числа необходимо знать его значение в радианах или градусах и использовать соответствующую формулу.
Все эти примеры демонстрируют важность формулы вычисления синуса числа и ее роли в решении различных математических и прикладных задач.