Вычисление синуса внешнего угла формулы является важным навыком в математике и физике. Он пригодится при решении различных задач, связанных с геометрией и тригонометрией. Но как это сделать правильно? В этой статье мы рассмотрим несколько полезных советов и техник, которые помогут вам вычислить синус внешнего угла формулы без проблем.
Прежде всего, необходимо знать, что внешний угол формулы - это угол, расположенный снаружи фигуры и образованный продолжением одной из ее сторон и продолжением другой стороны внутрь фигуры. Чтобы вычислить синус такого угла, можно воспользоваться связью между внешним и внутренним углами формулы, которая гласит: синус внешнего угла равен синусу внутреннего угла, дополнительному к внешнему углу.
Например, пусть у нас есть треугольник со сторонами a, b и c, где c - гипотенуза. Его внутренний угол A равен 45 градусов. Чтобы вычислить синус внешнего угла B, нам нужно найти дополнительный угол к нему. В данном случае это угол 180 - 45 = 135 градусов. Воспользовавшись связью, мы получим: синус внешнего угла B равен синусу угла 135 градусов.
Основы вычисления внешнего угла
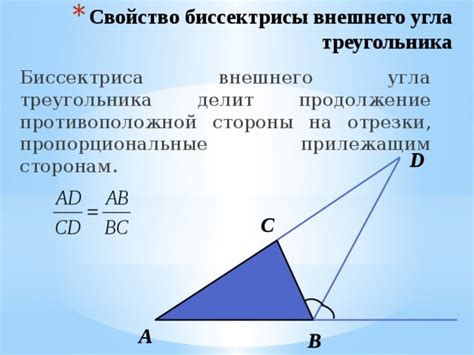
Для вычисления синуса внешнего угла можно использовать различные методы, в зависимости от задачи и известных данных. Одним из наиболее распространенных методов является использование тригонометрических функций.
Сначала необходимо определить угол, для которого нужно вычислить синус. Если угол измеряется в градусах, то его значение следует перевести в радианы, так как тригонометрические функции принимают аргументы в радианах.
Затем используя формулу синуса, можно вычислить синус внешнего угла. Формула синуса имеет вид: sin(внешний угол) = sin(180 - угол).
Полученное значение синуса можно использовать для решения задач, требующих вычисления синуса внешнего угла. Например, с помощью синуса можно определить длину стороны фигуры или вычислить площадь треугольника.
Вычисление внешнего угла является важным инструментом в математике и имеет множество применений в различных областях. Понимание основных принципов и техник вычисления внешнего угла поможет решать задачи более эффективно и достигать точности в результатах.
Понимание синуса
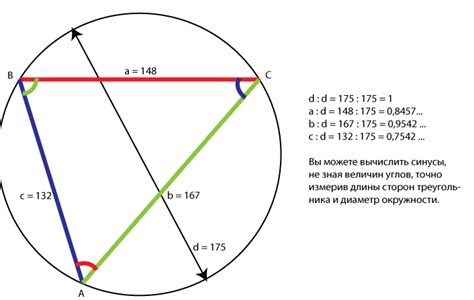
Синус внешнего угла формулы может быть вычислен с помощью специальных техник и методов. Одним из способов является использование тригонометрических соотношений и формул.
Для вычисления синуса внешнего угла формулы, необходимо знать значения синусов и косинусов внутренних углов треугольника, а также значения сторон треугольника. Эти значения могут быть получены с помощью формулы синусов или косинусов.
Понимание синуса и его связи с углами и сторонами треугольника может помочь в расчетах и решении различных задач, связанных с геометрией и тригонометрией. Глубокое понимание синуса позволяет использовать его не только для вычисления внешних углов треугольника, но и для решения других математических задач.
Использование синуса внешнего угла формулы может быть полезным инструментом для студентов и профессионалов в различных областях, таких как физика, инженерия и геометрия.
Важно помнить:
- Синус внешнего угла формулы может быть вычислен с использованием тригонометрических соотношений.
- Знание значений сторон и углов треугольника позволяет применять формулу синусов или косинусов для вычисления синуса внешнего угла.
- Понимание синуса и его связи с геометрическими фигурами может быть полезным для решения различных математических задач.
Использование техник и методов для вычисления синуса внешнего угла формулы позволяет решать задачи с высокой точностью и эффективностью.
Формула для вычисления внешнего угла
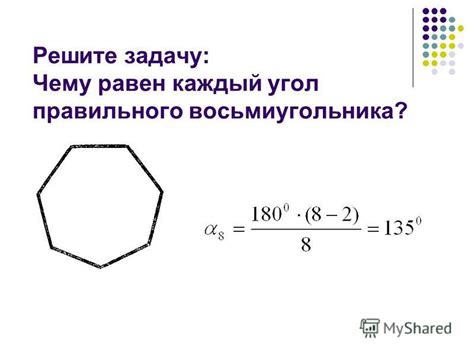
- Найдите значение внутреннего угла формулы с помощью известных данных.
- Положите значение внутреннего угла равным θ.
- Используйте формулу: внешний угол = 180° - θ, чтобы найти величину внешнего угла формулы.
Например, если внутренний угол формулы равен 40°, то внешний угол будет равен 180° - 40° = 140°.
Эта формула применима к различным видам фигур, таким как треугольники, прямоугольники, квадраты и многоугольники. Она позволяет точно вычислить величину внешнего угла формулы на основе известных данных о внутренних углах.
Вычисление внешнего угла формулы является важной задачей в геометрии и может быть использовано для решения различных задач и нахождения неизвестных значений углов.
Практические примеры

Ниже приведены несколько практических примеров, которые помогут вам вычислить синус внешнего угла формулы:
Пример 1: Вычислите синус внешнего угла формулы \(\sin(\theta + 2\pi)\).
Для решения этой задачи нужно знать, что синус периодична с периодом \(2\pi\). Таким образом, синус любого угла, увеличенного на \(\theta\), будет равен синусу исходного угла.
Поэтому \(\sin(\theta + 2\pi) = \sin(\theta)\).
Пример 2: Вычислите синус внешнего угла формулы \(\sin(2\pi - \theta)\).
Синус является четной функцией, поэтому \(\sin(2\pi - \theta) = -\sin(\theta)\).
Это означает, что синус внешнего угла формулы равен отрицательному значению синуса исходного угла.
Пример 3: Вычислите синус внешнего угла формулы \(\sin\left(\frac{\pi}{2} - \theta
ight)\).
Для решения этой задачи можно воспользоваться тригонометрической формулой синуса разности: \(\sin(A - B) = \sin(A)\cos(B) - \cos(A)\sin(B)\).
Применяя эту формулу, получим:
\(\sin\left(\frac{\pi}{2} - \theta
ight) = \sin\left(\frac{\pi}{2}
ight)\cos(\theta) - \cos\left(\frac{\pi}{2}
ight)\sin(\theta) = 1\cdot\cos(\theta) - 0\cdot\sin(\theta) = \cos(\theta)\).
Надеемся, что эти примеры помогут вам лучше разобраться в вычислении синуса внешнего угла формулы и применении соответствующих тригонометрических формул.
Техники вычисления

Вычисление синуса внешнего угла формулы может быть достаточно сложной задачей. Однако существуют различные техники, которые могут помочь вам в этом процессе:
- Используйте геометрическое представление: представьте себе треугольник с внешним углом формулы. Определите длины сторон треугольника и используйте соответствующие геометрические соотношения для определения синуса этого угла.
- Используйте тригонометрическую формулу: синус внешнего угла формулы можно выразить через синусы и косинусы внутренних углов. Используйте соответствующие тригонометрические тождества для вычисления синуса.
- Используйте таблицы или калькуляторы: существуют таблицы и калькуляторы, которые могут вычислить синус для вас. Воспользуйтесь ими для получения точного значения синуса внешнего угла формулы.
- Используйте программные инструменты: существуют программные инструменты, которые могут вычислить синус внешнего угла формулы за вас. Используйте эти инструменты для получения точного значения синуса.
Выберите технику, которая наиболее подходит вам и вашим потребностям, и используйте ее для вычисления синуса внешнего угла формулы.
Советы по использованию формулы

При использовании формулы для вычисления синуса внешнего угла необходимо учитывать следующие советы:
- Угол должен быть в радианах: перед использованием формулы необходимо убедиться, что угол задан в радианах, так как формула для вычисления синуса принимает значение угла в радианах.
- Проверить диапазон углов: угол должен находиться в диапазоне от 0 до 2π (или от 0 до 360 градусов), чтобы формула корректно вычисляла его синус. Если угол находится за пределами этого диапазона, необходимо привести его к заданному диапазону.
- Использовать точные значения: для более точных вычислений синуса внешнего угла можно использовать таблицу значений синуса или использовать математические функции для расчета.
- Учесть свойства синуса: синус является периодической функцией, поэтому для более сложных вычислений можно использовать свойства синуса, такие как симметрия, периодичность и тригонометрические тождества.
Следуя этим советам, можно эффективно использовать формулу для вычисления синуса внешнего угла и получить более точные результаты. Удачных расчетов!