Одной из важных свойств математических функций является симметрия относительно начала координат. Это значит, что график функции при некоторых условиях обладает определенной геометрической структурой, что позволяет упростить ее анализ и применение в различных областях науки и техники.
Симметрия является важным свойством функций и встречается во многих ее разновидностях. Например, симметричными могут быть линейные, квадратичные, показательные, тригонометрические функции и другие. Для определения симметрии функции необходимо анализировать ее уравнение и график на наличие определенных закономерностей.
Если функция симметрична относительно начала координат, то это означает, что при замене координат (x, y) на (-x, -y) уравнение функции остается неизменным. Другими словами, график функции отражается относительно начала координат и сохраняет свою форму. Это свойство позволяет существенно упростить анализ функции и найти дополнительные ее характеристики.
Понятие и определение
Математический признак симметрии функции относительно начала координат можно записать следующим образом:
| Условие симметрии: | y = f(x) | ⟺ | y = f(-x) |
|---|
То есть, для любого значения аргумента x функция f(x) равна функции f(-x), что приводит к симметрии относительно начала координат.
Примеры функций с симметрией относительно начала координат
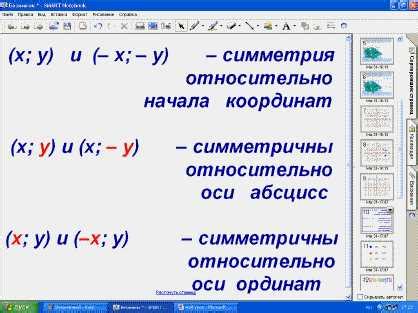
Функция, симметричная относительно начала координат, имеет свойство сохранения своей формы при замене аргумента на его противоположное значение.
Вот несколько примеров таких функций:
1. Функция вида y = xn
При нечетном значении n функция будет симметрична относительно начала координат. Каждый положительный x будет иметь соответствующий отрицательный x, дающий тот же результат. Например, если у = x3, то y(-1) = (-1)3 = -1, а y(1) = 13 = 1.
2. Функция вида y = cos(x)
Функция cos(x) является симметричной относительно начала координат. Значения cos(x) для положительных и отрицательных x равны по модулю, но имеют противоположные знаки. Например, cos(-π) = cos(π) = -1.
3. Функция вида y = |x|
Функция |x| имеет симметрию относительно начала координат. Значение функции для положительного x будет таким же, как и для отрицательного x с противоположным знаком. Например, |(-2)| = 2 и |2| = 2.
Это лишь несколько примеров функций, обладающих симметрией относительно начала координат. В общем случае, функция будет симметрична, если выполняется условие f(x) = f(-x) для всех x в области определения функции.
Свойства функций с симметрией относительно начала координат
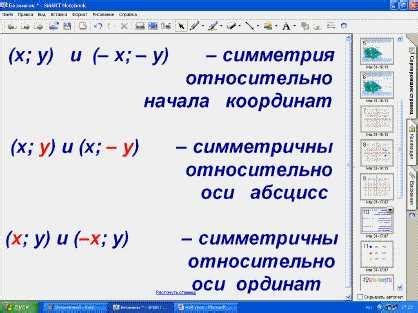
- Симметрия: если точка (x, y) принадлежит графику функции, то точка (-x, -y) также принадлежит графику функции. Это означает, что график функции симметричен относительно начала координат.
- Нечетность: функции с симметрией относительно начала координат являются нечетными. Это означает, что для любого значения x, значение функции f(x) равно -f(-x). Например, если f(2) = 5, то f(-2) = -5.
- Ноль в нуле: такие функции обладают нулевым значением в начале координат. Это означает, что f(0) = 0.
- Отношение квадратов: если функция f(x) симметрична относительно начала координат, то ее график можно представить как график функции g(x) = x^2. То есть f(x) = g(x) для любого x.
- Инвертирование графика: если график функции f(x) является графиком функции g(x), то график функции -f(x) является инвертированным графиком функции g(x).
Функции с симметрией относительно начала координат являются важными объектами изучения в математике и имеют широкий спектр применений. Они позволяют нам легче анализировать графики функций и строить математические модели для различных явлений и задач.
Геометрическая интерпретация симметрии относительно начала координат
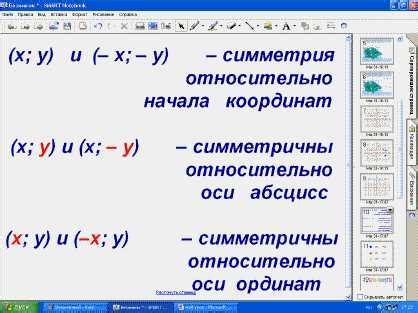
Когда функция симметрична относительно начала координат, ее график может быть прокомментирован следующим образом:
1. Если точка принадлежит графику функции, то ее симметричная относительно начала координат точка также будет принадлежать графику функции.
2. Если точка лежит на оси абсцисс или оси ординат и принадлежит графику функции, то ее симметричная относительно начала координат точка также будет принадлежать графику функции.
3. Если точка принадлежит графику функции, а ее абсцисса или ордината отрицательны, то симметричная относительно начала координат точка также будет принадлежать графику функции, но с противоположным знаком координаты.
4. Если точка принадлежит графику функции, а ее абсцисса или ордината равны нулю, то соответствующая симметричная относительно начала координат точка также будет принадлежать графику функции, но с противоположным знаком координаты.
Таким образом, геометрическая интерпретация симметрии относительно начала координат позволяет анализировать свойства функции и ее графика на основе симметричных отношений относительно начала координат в декартовой системе координат.
Приложения функций с симметрией относительно начала координат в науке и технике
В физике функции с симметрией относительно начала координат могут использоваться, например, для описания симметрии распределения заряда или массы. Это позволяет упростить расчеты и провести анализ особенностей электрических или гравитационных полей, например, вокруг симметрично расположенных зарядов или массивов.
В технике функции с симметрией относительно начала координат могут использоваться для упрощения проектирования, анализа или моделирования различных систем и устройств. Например, при проектировании симметричных антенн или камеры отражения, для расчета поля или изображения можно использовать функции с симметрией относительно начала координат.
Также функции с симметрией относительно начала координат широко применяются в математическом моделировании и компьютерной графике. Они помогают создавать реалистичные и эффективные алгоритмы, например, для генерации симметричных фрактальных структур или обработки изображений.