Функция синус – одна из самых известных и широко применяемых тригонометрических функций. Она является периодической и гладкой функцией, которая определена для всех действительных чисел.
Основное свойство синуса – его периодичность. Значение синуса повторяется через равные промежутки. Если мы рассматриваем синус при углах, выраженных в радианах, то его период равен 2π. Это значит, что при углах от 0 до 2π значения синуса повторяются. Например, синус 0 равен 0, синус π/2 равен 1, синус π равен 0, синус 3π/2 равен -1 и так далее.
Функция синус обладает также свойством симметрии. Синус угла равен синусу симметричного относительно начала координат угла. Например, синус угла α равен синусу угла -α. Это свойство можно интуитивно понять, если представить себе график синуса, который симметричен относительно оси OY.
Роль синуса в математике и физике
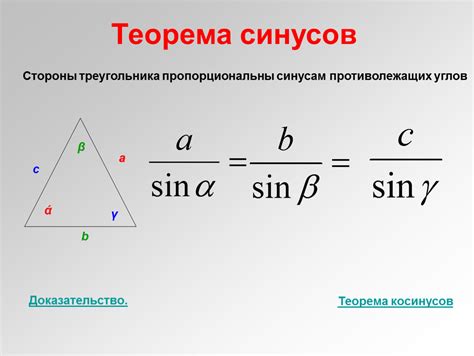
В математике синус играет важную роль в решении геометрических задач, обработке сигналов, анализе колебаний и волн. Он широко применяется в алгебре, геометрии, анализе и других областях математики. Синус также является ключевой функцией в теории дифференциальных уравнений и некоторых областях математической физики.
В физике синус используется для описания периодических явлений, таких как колебания, волны и сигналы. Он помогает предсказывать и анализировать поведение систем, имеющих периодические осцилляции. Например, синус используется для описания движения маятника, звуковых волн, электромагнитных колебаний и других физических процессов.
Также синус имеет много полезных свойств, которые позволяют использовать его в различных расчетах и формулах. Например, синус участвует в определении площади треугольника, законе Синусов, а также в формулах для преобразования между прямоугольными и полярными координатами.
Основные свойства синуса
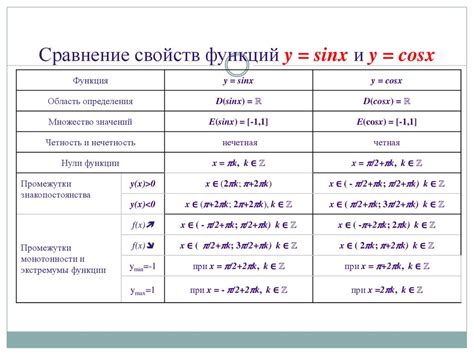
Основные свойства синуса:
| Симметрия синуса: | Синус является нечетной функцией, что означает, что для любого аргумента x справедливо равенство sin(-x) = -sin(x). Это свойство подразумевает, что значение синуса симметрично относительно оси ординат. |
| Периодичность: | Синус имеет период 2π, что означает, что его значение повторяется при приращении аргумента на это значение. То есть sin(x + 2π) = sin(x) для любого значения x. |
| Значения на основных углах: | На основных углах, таких как 0°, 30°, 45°, 60°, 90° и т.д., синус имеет определенные значения, которые могут быть вычислены точно или приближенно. |
| Зависимость от косинуса и тангенса: | Синус связан с косинусом и тангенсом следующими соотношениями: sin(x) = cos(π/2 - x) и sin(x) = tan(x)/sec(x). |
Это лишь некоторые из важных свойств синуса, которые позволяют использовать эту функцию в различных математических и физических задачах.
Симметрия синуса и ее значения
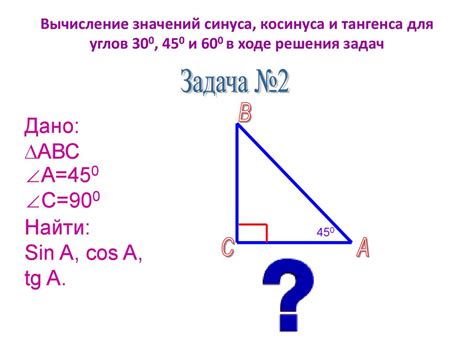
Например, sin(-x) = -sin(x), где x - любое значение угла.
Это свойство симметрии позволяет использовать значения синуса для отрицательных углов, определяя их через положительные углы. Таким образом, мы можем упростить вычисления и получить точные значения для широкого диапазона углов.
Кроме того, синус обладает периодической симметрией, что означает, что значения функции повторяются через определенные интервалы. Точнее, синус имеет период равный 360 градусам или 2π радианам.
Это означает, что sin(x) = sin(x + 360°) = sin(x + 2π), где x - любое значение угла.
Значения синуса симметричны относительно оси ординат. График функции изображает периодическую кривую, которая проходит через нули в точках x = 0, x = 180° (π), x = -180° (-π), и т.д.
Симметрия синуса позволяет использовать его для решения широкого круга задач, связанных с колебаниями, звуком, электрическими и механическими волнами, а также в обработке сигналов и многих других областях науки и техники.
Применение синуса в решении задач
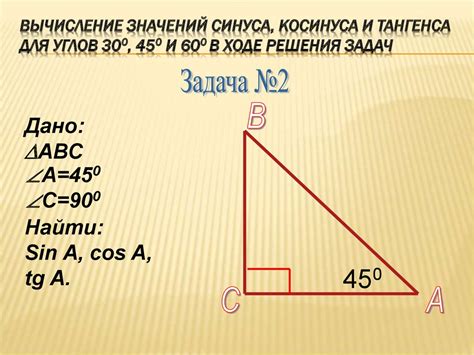
Функция синус имеет широкое применение в различных областях, включая математику, физику, астрономию и инженерные науки. Ее свойства и симметрия позволяют использовать ее в решении различных задач.
Синус может быть использован для вычисления углов и длин сторон треугольников. Например, если известны длины двух сторон треугольника и величина их международный угла, то можно использовать функцию синус для вычисления длины третьей стороны.
Функция синус также может быть использована для моделирования колебаний и волн. Например, при изучении звуковых волн и световых волн, синус может быть использован для описания амплитуды и фазы колебаний.
Синус также может быть использован в решении задач на определение расстояния и высоты. Например, синус может быть применен для измерения высоты недоступного объекта на основе высоты и длины тени, а также для определения расстояния до объекта на основе известного угла наблюдения.
Таким образом, функция синус является мощным математическим инструментом, который может быть использован для решения различных задач, связанных с треугольниками, колебаниями и измерениями. Понимание свойств и симметрии синуса позволяет применять его эффективно и точно в различных областях науки и техники.