Гипотезы делятся на два типа: нулевые и альтернативные. Нулевая гипотеза предполагает, что никаких значимых различий или эффектов нет, тогда как альтернативная гипотеза подразумевает наличие каких-либо значимых отклонений от нулевой гипотезы.
Определение и основные принципы
Основными принципами гипотез в теории вероятности являются:
- Постановка гипотезы: определение предположения о вероятностных свойствах случайных явлений.
- Формулировка нулевой и альтернативной гипотезы: нулевая гипотеза содержит утверждение о равенстве или отсутствии различий между группами, а альтернативная гипотеза предполагает наличие различий или эффекта.
- Выбор уровня значимости: определение уровня риска, который готовы принять исследователи при отклонении нулевой гипотезы.
- Сбор и анализ данных: сбор данных и проведение статистического анализа для проверки гипотезы.
- Интерпретация результатов: объяснение полученных результатов и их значимости с точки зрения изначальной гипотезы.
| Принцип | Описание |
|---|---|
| Постановка гипотезы | Определение предположения о вероятностных свойствах случайных явлений. |
| Формулировка нулевой и альтернативной гипотезы | Нулевая гипотеза содержит утверждение о равенстве или отсутствии различий между группами, а альтернативная гипотеза предполагает наличие различий или эффекта. |
| Выбор уровня значимости | Определение уровня риска, который готовы принять исследователи при отклонении нулевой гипотезы. |
| Сбор и анализ данных | Сбор данных и проведение статистического анализа для проверки гипотезы. |
| Статистическое решение | |
| Интерпретация результатов | Объяснение полученных результатов и их значимости с точки зрения изначальной гипотезы. |
Шаг за шагом к пониманию гипотез
- Определение гипотезы: гипотеза - это предположение или утверждение о параметрах или свойствах генеральной совокупности, которые проверяются на основе доступных данных.
- Формулировка нулевой и альтернативной гипотез: нулевая гипотеза (H0) - это предположение, что ни одно статистическое отличие не существует между группами или наблюдаемыми данными. Альтернативная гипотеза (H1) предполагает существование статистического отличия или эффекта.
- Выбор уровня значимости: уровень значимости (α) определяет, какую вероятность мы готовы принять в качестве критической для отклонения нулевой гипотезы. Обычно выбирают уровень значимости 0.05 или 0.01.
- Выбор статистического критерия: выбор статистического критерия зависит от типа данных и наличия или отсутствия предположений о распределении.
- Вычисление статистического значения: с помощью выбранного статистического критерия вычисляется статистическое значение на основе доступных данных.
- Принятие решения: на основе статистического значения и уровня значимости принимается решение о принятии или отклонении нулевой гипотезы. Если статистическое значение меньше уровня значимости, то отклоняем нулевую гипотезу.
Расчеты и проверка гипотез в теории вероятности
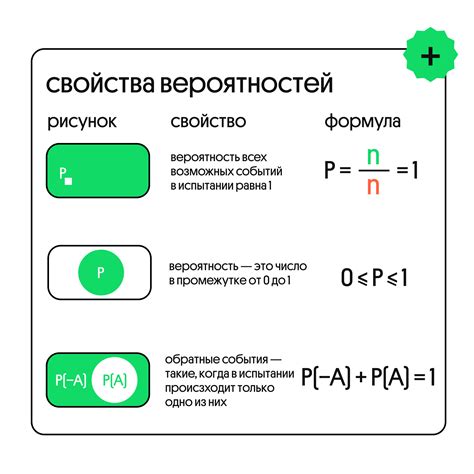
В теории вероятности, расчеты и проверка гипотез играют важную роль в понимании и предсказании случайных явлений. Расчеты позволяют определить вероятность наступления определенного события или наблюдаемых результатов, а проверка гипотез позволяет сравнить реальные данные со статистическими моделями и установить, насколько данные соответствуют или не соответствуют теоретическим предположениям.
Расчеты вероятностей могут быть выполнены с использованием различных методов, включая комбинаторику, геометрические и статистические подходы. Важным шагом в расчетах вероятностей является определение пространства элементарных исходов и событий, а также их вероятностей.
Проверка гипотез основана на сравнении наблюдаемых данных с нулевой гипотезой, которая предполагает отсутствие различий или влияния факторов. Для этого используются различные статистические методы, включая t-тест, анализ дисперсии и хи-квадрат тест.
Расчеты и проверка гипотез в теории вероятности могут быть полезными инструментами для принятия решений и предсказания вероятности событий. Они применяются в различных областях, включая физику, экономику, медицину и социальные науки.