Графики функций являются важным инструментом в математике. Они позволяют наглядно представить зависимость между переменными и исследовать различные свойства функций. Одной из интересных и полезных функций является обратная функция.
Обратная функция - это функция, которая действует в обратном направлении по отношению к исходной функции. Другими словами, если мы знаем значение функции f(x), то по обратной функции мы можем найти значение x. Обратная функция обозначается как f-1(x).
Особенностью графика обратной функции является то, что он симметричен по отношению к прямой y = x. Это означает, что точки на графике исходной функции и обратной функции являются зеркальными отражениями друг друга относительно этой прямой.
Для наглядного представления особенностей графика обратной функции, рассмотрим пример. Пусть исходная функция f(x) = 2x. Тогда обратная функция f-1(x) будет равна f-1(x) = x/2. Если построить график функции f(x) = 2x и его обратной функции, мы увидим, что они действительно являются зеркальными отражениями друг друга относительно прямой y = x.
График обратной функции
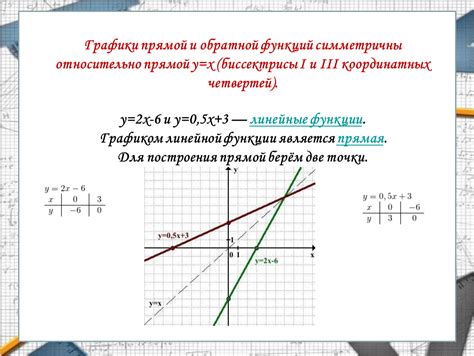
График обратной функции имеет особые особенности и отличается от графика исходной функции. Во-первых, график обратной функции симметричен относительно прямой y = x. Это означает, что если точка (a, b) принадлежит графику функции f(x), то точка (b, a) принадлежит графику обратной функции f-1(x).
Во-вторых, график обратной функции находится в тех же координатах, что и график исходной функции, но их позиции меняются относительно оси абсцисс и оси ординат. Если график исходной функции растет слева направо, то график обратной функции будет расти снизу вверх.
Примером графика обратной функции может быть график параболы y = x2. График этой функции выглядит как парабола, которая открывается вверх. Ее обратная функция будет выглядеть так: y = √x. График обратной функции будет представлять собой положительную ветвь параболы, которая открывается вправо и имеет ось симметрии, соответствующую прямой y = x.
Особенности и примеры
Одной из особенностей графика обратной функции является то, что он симметричен относительно функции f(x). Если график функции f(x) имеет точку с координатами (x, y), то график обратной функции f^(-1)(x) будет иметь точку с координатами (y, x).
Например, пусть у нас есть функция f(x) = 2x. График этой функции представляет собой прямую линию, проходящую через начало координат и имеющую положительный наклон. График обратной функции f^(-1)(x) будет также прямой линией, но с отрицательным наклоном и симметричной относительно оси y.
Примером другой функции может быть f(x) = x^2. График этой функции представляет собой параболу, открывающуюся вверх и с вершиной в начале координат. График обратной функции f^(-1)(x) будет представлять собой параболу, открывающуюся влево или вправо в зависимости от выбора направления перпендикуляра к оси x в начале координат.
График обратной функции имеет свои особенности, которые следует учитывать при анализе функций и их обратных отношений. Понимание этих особенностей помогает не только в визуализации математических концепций, но и в решении практических задач.