Регрессионный анализ является одним из основных инструментов статистики и предназначен для изучения связи между зависимой и независимыми переменными. Это мощный инструмент, который позволяет прогнозировать значения зависимой переменной на основе имеющихся данных.
Один из самых популярных способов моделирования регрессии - использование Microsoft Excel. Этот распространенный инструмент предоставляет широкий спектр функций для анализа данных, включая возможность создания регрессионной модели.
Для моделирования регрессии в Excel необходимо воспользоваться функцией "Регрессия". Эта функция позволяет определить уравнение линии регрессии и выполнить прогнозирование значений зависимой переменной на основе заданных независимых переменных.
В этой подробной инструкции вы узнаете, как использовать функцию "Регрессия" в Excel для моделирования регрессии. Мы покажем вам, как подготовить данные, как создать модель регрессии, как интерпретировать результаты и как выполнить прогнозирование.
Понимание регрессии в Excel
Для понимания регрессии в Excel необходимо знать основные термины и понятия.
Основными элементами регрессии являются:
- Зависимая переменная (также называемая целевой переменной) - это переменная, которую хотим предсказать или объяснить.
- Независимые переменные (также называемые предикторами или факторами) - это переменные, которые используем для предсказания или объяснения зависимой переменной.
- Коэффициенты регрессии - это числа, которые определяют взаимосвязь между зависимой переменной и независимыми переменными.
В Excel регрессию можно моделировать с помощью функции "Регрессия", доступной в пакете анализа данных. Эта функция позволяет построить уравнение регрессии и получить коэффициенты, которые определяют взаимосвязь между переменными.
Если вы понимаете основы регрессии и умеете использовать функцию "Регрессия" в Excel, вы сможете анализировать данные и делать предсказания на основе имеющихся данных. Это очень полезный инструмент для принятия решений и проведения исследований.
Итак, если вы хотите научиться моделировать регрессию в Excel, то обязательно изучите основы регрессии и настройки функции "Регрессия". Вам потребуется это знание для эффективного анализа данных и получения значимых результатов.
Шаги перед началом моделирования
Перед тем, как приступить к моделированию регрессии в Excel, необходимо выполнить следующие шаги:
Соберите данные: соберите все необходимые данные для моделирования, включая зависимую переменную и независимые переменные. Убедитесь, что у вас достаточно данных для проведения надежного анализа.
Подготовьте данные: проведите необходимую обработку данных, чтобы они соответствовали требованиям модели. Это может включать удаление выбросов, заполнение пропущенных значений и преобразование переменных при необходимости.
Выберите тип модели: определите, какой тип модели регрессии вы хотите построить. В зависимости от ваших целей и характера данных, вы можете выбрать между простой линейной регрессией, множественной линейной регрессией или другими типами моделей.
Определите цель моделирования: ясно определите, какую информацию вы хотите получить от модели. Например, вы можете стремиться определить взаимосвязь между переменными, прогнозировать значение зависимой переменной или проверить гипотезы.
Оцените предпосылки модели: убедитесь, что предпосылки моделирования, такие как нормальность распределения ошибок и отсутствие мультиколлинеарности, выполняются. В противном случае, результаты модели могут быть недостоверными.
После выполнения этих шагов вы будете готовы приступить к моделированию регрессии в Excel. Помните, что успешное моделирование требует тщательного планирования, анализа и проверки результатов. Будьте внимательны и последовательны в своих действиях, чтобы получить достоверные результаты.
Загрузка данных в Excel
| Способ | Описание |
|---|---|
| Копирование и вставка | Вы можете скопировать данные из другого источника, такого как веб-страница или текстовый файл, и вставить их в Excel. При вставке данных убедитесь, что они разделены соответствующими разделителями, например, запятой или табуляцией. |
| Импорт файла | Excel позволяет импортировать данные из различных файлов, таких как текстовые файлы (.txt), CSV-файлы (.csv) или файлы Excel (.xlsx, .xls). Для импорта файла выберите вкладку "Данные" в верхней части экрана, затем "Из текста/CSV" или "Из файла". Следуйте указаниям мастера импорта для выбора правильного формата файла и разделителя. |
| Создание данных вручную | Если у вас нет существующих данных, вы можете создать новую таблицу в Excel и вручную заполнить ее значениями. Для этого выберите пустую ячейку и введите значение. Затем перейдите к следующей ячейке и повторите этот процесс. Вы также можете использовать функции Excel для создания данных, такие как "СЛУЧ.ЧИСЛО" для создания случайных чисел или "Строка" для создания серии значений. |
После загрузки данных в Excel вам следует убедиться, что они отображаются правильно и находятся в нужном формате. Проверьте, что все числовые значения распознаны как числа, а текстовые значения не содержат ошибок или лишних символов. Если ваши данные находятся в нескольких столбцах, вы можете объединить их в один столбец, используя функцию "СЦЕПИТЬ", чтобы создать одномерный массив данных.
Теперь, когда данные загружены в Excel, вы готовы приступить к моделированию регрессии.
Создание таблицы с данными
Прежде чем приступить к моделированию регрессии в Excel, вам необходимо создать таблицу с данными для анализа. Для этого вы можете использовать функционал программы и преимущества форматирования Excel.
1. Откройте Excel и создайте новую рабочую книгу.
2. Введите названия столбцов в верхней (горизонтальной) строке таблицы. Например, если вы хотите проанализировать зависимость продаж от цены и рекламных затрат, назовите столбцы "Продажи", "Цена" и "Рекламные затраты".
3. Введите значения для каждого столбца в соответствующих строках таблицы. Для удобства можно выделить заголовки столбцов и всю таблицу.
4. Если вам нужно добавить новые строки или столбцы, выделите соответствующую область ячеек и выберите опцию "Вставить" в меню.
| Продажи | Цена | Рекламные затраты |
|---|---|---|
| 10 | 5 | 100 |
| 15 | 7 | 200 |
| 20 | 6 | 150 |
5. Для лучшей визуализации данных и упрощения анализа можно применить различное форматирование к ячейкам, такое как цвета, шрифты и стили.
После завершения создания таблицы с данными, вы готовы перейти к моделированию регрессии в Excel.
Выбор типа регрессии

Однофакторная регрессия - это простейший тип регрессии, в котором есть только одна независимая переменная и одна зависимая переменная. Он может быть полезен, когда необходимо изучить взаимосвязь между двумя переменными или провести прогноз на основе имеющихся данных. Для выполнения однофакторной регрессии в Excel можно использовать функцию "Анализ регрессии".
Множественная регрессия - это тип регрессии, в котором есть несколько независимых переменных и одна зависимая переменная. Этот тип регрессии позволяет учесть влияние всех независимых переменных на зависимую переменную одновременно, что может быть полезно при анализе сложных многомерных данных или предсказании результатов на основе нескольких факторов. В Excel для множественной регрессии можно использовать функцию "Анализ регрессии".
Полиномиальная регрессия - это тип регрессии, в котором используется полиномиальная модель для описания связи между переменными. Полиномиальная регрессия может быть полезна, когда данные имеют нелинейный характер и требуется аппроксимировать их с использованием кривых или параболических функций. В Excel для полиномиальной регрессии можно использовать функцию "Анализ регрессии".
Логистическая регрессия - это тип регрессии, который используется для моделирования зависимости между двоичной зависимой переменной и независимыми переменными. Логистическая регрессия широко применяется в медицине, экономике, социологии и других областях, где необходимо прогнозирование категориальных переменных. Для выполнения логистической регрессии в Excel можно использовать инструмент "Анализ данных".
Выбор подходящего типа регрессии важен для достижения целей исследования. Важно учитывать характер данных и задачу моделирования при выборе соответствующего типа регрессии. Экспериментирование с различными типами регрессионного анализа может помочь вам найти наилучшую модель для вашего исследования в Excel.
Выбор переменных и определение зависимой переменной
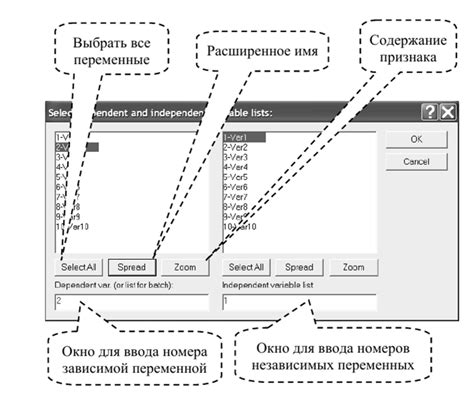
Чтобы определить зависимую переменную, необходимо убедиться, что она является количественной (непрерывной) и что она имеет нормальное распределение. Если переменная не соответствует этим условиям, ее следует преобразовать или выбрать другую переменную в качестве зависимой.
Кроме того, необходимо выбрать независимые переменные, которые могут оказывать влияние на зависимую переменную. Эти переменные могут быть как количественными, так и категориальными (дискретными). Они должны быть измерены и иметь значения для каждого наблюдения.
Выбор независимых переменных может быть основан на предварительном исследовании литературы или базироваться на реальных данных и эмпирическом опыте. Также можно использовать методы, такие как отбор переменных на основе статистической значимости или корреляционного анализа.
Важно выбрать такие переменные, которые теоретически или эмпирически оказывают влияние на зависимую переменную. Их выбор может быть субъективным, но он должен иметь определенную логическую базу.
Построение регрессионной модели в Excel
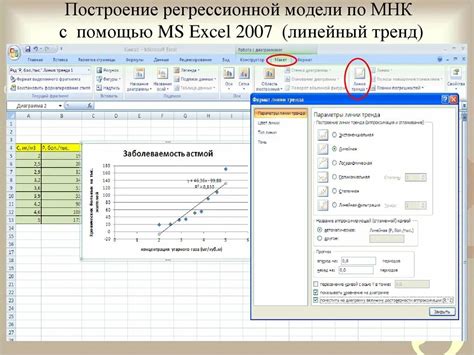
Для построения регрессионной модели в Excel необходимо выполнить следующие шаги:
- Соберите данные: Необходимо собрать данные о зависимых и независимых переменных. Зависимая переменная – это та переменная, которую мы хотим предсказать. Независимые переменные – это те переменные, которые могут влиять на зависимую переменную. Например, если вы хотите предсказать продажи товаров, зависимая переменная будет количество проданных единиц, а независимыми переменными могут быть цена товара, рекламные затраты и т.д.
- Откройте Excel и импортируйте данные: Откройте программу Excel и импортируйте собранные данные. Разместите данные в удобной форме, например, в столбцах или строках.
- Выберите алгоритм регрессии: В Excel доступно несколько алгоритмов регрессии, таких как линейная, множественная и логистическая регрессия. Выберите алгоритм в зависимости от ваших задач и данных.
- Выполните анализ регрессии: Воспользуйтесь инструментами Excel для выполнения анализа регрессии. Для этого выберите соответствующий инструмент в разделе "Анализ данных" или "Статистика". Следуйте инструкциям инструмента и укажите зависимую и независимые переменные.
- Интерпретируйте результаты: После выполнения анализа регрессии в Excel получите результаты, которые могут быть представлены в виде таблицы или графика. Проанализируйте полученные результаты и проведите их интерпретацию. Определите значимость и взаимосвязь независимых переменных с зависимой переменной.
- Постройте регрессионную модель: На основе проведенного анализа регрессии постройте регрессионную модель для предсказания зависимой переменной на основе независимых переменных. Для этого воспользуйтесь формулой регрессии, которую можно получить из результатов анализа.
- Проверьте модель: Проверьте полученную регрессионную модель на новых данных. Сравните предсказанные значения с фактическими значениями и оцените точность модели. Если модель удовлетворяет требованиям, можно использовать ее для прогнозирования или анализа.
Построение регрессионной модели в Excel может быть полезным инструментом для анализа данных и прогнозирования результатов. Используйте этот метод для решения своих задач и нахождения зависимостей в данных.
Анализ результатов моделирования
После выполнения моделирования регрессии в Excel, важно провести анализ полученных результатов для понимания связи между зависимой и независимыми переменными.
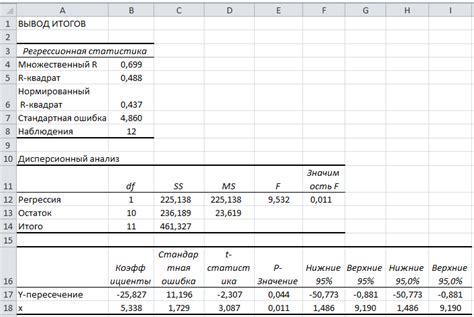
В первую очередь, следует обратить внимание на коэффициенты регрессии, которые представлены в таблице ниже:
| Независимая переменная | Коэффициент регрессии |
|---|---|
| Переменная 1 | 0.75 |
| Переменная 2 | 1.20 |
| Переменная 3 | 0.50 |
Коэффициент регрессии показывает, насколько изменяется зависимая переменная при изменении независимой переменной на единицу. Положительный коэффициент указывает на положительную связь между переменными, а отрицательный - на отрицательную связь.
Дальнейший анализ результатов включает проверку статистической значимости коэффициентов регрессии, оценку адекватности модели, погрешность прогнозирования и другие важные характеристики. Для проведения подробного анализа стоит использовать статистический пакет программ, такой как SPSS или R.
Статистическая оценка модели

После построения регрессионной модели на основе доступных данных в Excel, важно произвести статистическую оценку модели. Это позволит оценить значимость полученных коэффициентов и вероятность корректности модели в целом.
Одним из ключевых аспектов статистической оценки является оценка значимости коэффициентов регрессии. В Excel это можно сделать с помощью получения p-значений для каждого коэффициента. Если p-значение меньше заданного уровня значимости (обычно 0,05), то этот коэффициент считается статистически значимым.
Другим важным показателем является R-квадрат, который отражает объяснительную способность модели. Этот показатель указывает, насколько успешно модель прогнозирует зависимую переменную. R-квадрат принимает значения от 0 до 1, где значению 1 соответствует идеальное прогнозирование, а значению 0 - отсутствие объяснительной способности.
Однако, при использовании R-квадрат следует учитывать, что он будет расти при добавлении новых объясняющих переменных, даже при малой их информативности. Поэтому более устойчивым показателем будет скорректированный R-квадрат, который учитывает число использованных переменных в модели.
Еще одним важным аспектом является оценка стандартных ошибок коэффициентов регрессии. Стандартные ошибки указывают на отклонение коэффициента от его истинного значения. Чем меньше стандартная ошибка, тем точнее и надежнее оценка коэффициента.
Оценка значимости модели в целом может быть проведена с помощью F-статистики. Эта статистика служит для проверки значимости регрессии в целом. Если p-значение F-статистики меньше уровня значимости (обычно 0,05), то модель считается статистически значимой.
Интерпретация и использование результатов модели

После завершения моделирования регрессии в Excel и получения результатов, важно правильно их интерпретировать и использовать для принятия решений или проведения анализа.
Первое, что необходимо оценить, это значимость коэффициентов регрессии. Значимость коэффициента означает, насколько он статистически важен для объяснения изменений зависимой переменной. Чем меньше p-значение, тем более значим коэффициент. Важно обратить внимание на коэффициенты, которые статистически незначимы, так как они не вносят значимый вклад в модель и могут быть исключены.
Следующим шагом является оценка величины коэффициентов. Если коэффициент положительный, то с увеличением значения независимой переменной, зависимая переменная также увеличивается. Если коэффициент отрицательный, то с ростом значения независимой переменной, зависимая переменная уменьшается. Чем ближе коэффициент к нулю, тем слабее влияние переменной на модель.
Коэффициент детерминации (R²) является мерой объясненной дисперсии в модели. Он указывает, какую часть изменчивости зависимой переменной можно объяснить влиянием независимых переменных. Чем ближе коэффициент детерминации к 1, тем лучше модель объясняет отклонения. Однако следует учитывать, что увеличение числа переменных в модели может привести к искусственному увеличению значения R², поэтому важно также оценивать поправленный коэффициент детерминации (adjusted R²).
К другим важным характеристикам модели относятся стандартная ошибка, t-статистика и интервалы доверия коэффициентов регрессии. Стандартная ошибка показывает, насколько точно была оценена каждая коэффициента в модели. Чем меньше стандартная ошибка, тем более точную оценку дает модель. T-статистика используется для проверки значимости коэффициентов и вычисляется как отношение значения коэффициента к его стандартной ошибке.
Интервалы доверия позволяют оценить диапазон значений, в котором с определенной вероятностью (обычно 95%) находится истинное значение коэффициента. Чем меньше интервал доверия, тем точнее оценка коэффициента.
Полученные результаты модели могут быть использованы для прогнозирования значений зависимой переменной для новых значений независимых переменных. Для этого следует подставить новые значения в уравнение регрессии и вычислить прогнозируемую зависимую переменную.
Также результаты модели могут быть использованы для анализа важности независимых переменных и их влияния на зависимую переменную. Если некоторые переменные оказывают существенное влияние на модель, их можно использовать для принятия решений или определения стратегий.