Куб - это геометрическое тело, в котором все шесть граней равны между собой по площади и шестигранные углы прямые. Каждая грань куба является квадратом, а каждое ребро - отрезком, соединяющим две соседние вершины. Для определения суммы длин ребер куба можно использовать несколько методов.
Первый метод заключается в умножении длины одного ребра на количество ребер. Так как в кубе каждая вершина связана с тремя ребрами, а каждое ребро соседствует с двумя другими, количество ребер в кубе равно 12. Длина ребра куба может быть определена по формуле A = V^(1/3), где А - площадь грани, V - объем куба.
Второй метод предполагает нахождение суммы длин ребер, соединяющих каждую вершину куба с каждой другой вершиной. В кубе всего 8 вершин, поэтому необходимо посчитать длину ребра, соединяющего две вершины, и умножить ее на количество ребер, выходящих из каждой вершины, то есть на 3.
Параллелепипед - это геометрическое тело, все грани которого параллельны попарно. Для подсчета суммы длин ребер параллелепипеда необходимо использовать похожие методы.
Первый метод предлагает умножить длины трех ребер, выходящих из одной вершины, на количество вершин, то есть 8. Так как в параллелепипеде все шесть граней параллельны попарно, количество выходящих ребер равно 3 для каждой вершины.
Второй метод предполагает нахождение суммы длин ребер, выходящих из каждой вершины. Так как в параллелепипеде также 8 вершин, необходимо посчитать длину ребра, соединяющего две вершины, и умножить ее на количество ребер, выходящих из каждой вершины, то есть на 3.
Прямоугольный параллелепипед со сторонами разной длины
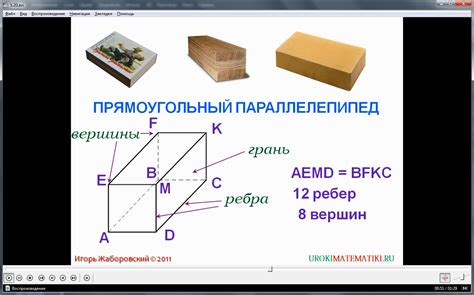
Если у прямоугольного параллелепипеда все стороны имеют разную длину, то такой параллелепипед называется неравносторонним.
Для нахождения суммы длин всех ребер неравностороннего параллелепипеда, нужно вычислить сумму всех его ребер. Сумма включает в себя длины всех ребер, которые являются ребрами параллелепипеда.
Для прямоугольного параллелепипеда со сторонами разной длины, сумма длин всех его ребер будет равна удвоенной сумме длин всех его ребер, так как каждое ребро имеет свое парное ребро, с такой же длиной.
Таким образом, сумма длин всех ребер неравностороннего прямоугольного параллелепипеда составляет двойную сумму длин всех его ребер.
Куб с одинаковыми сторонами
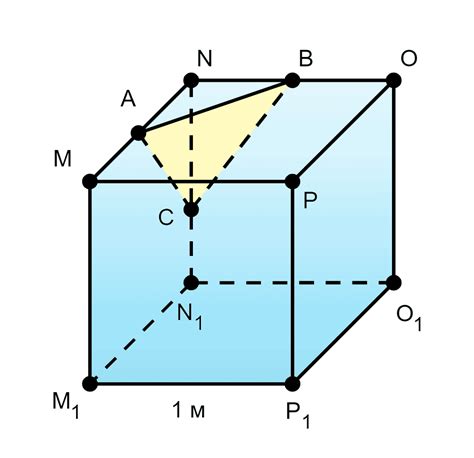
Для примера, предположим, что длина стороны куба составляет 5 см. Чтобы найти сумму длин всех ребер, нужно умножить 5 на 12, что даст нам результат равный 60 см.
Таким образом, для куба с одинаковыми сторонами можно использовать простую формулу: сумма длин ребер равняется длине одной стороны, умноженной на 12.
Параллелепипед со сторонами разной длины
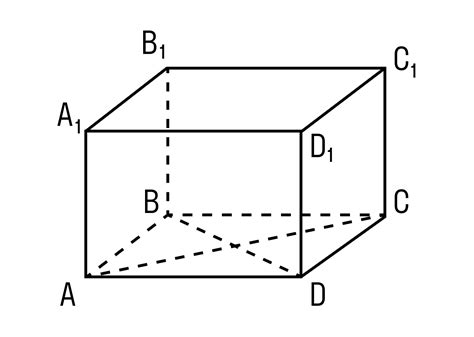
Однако часто встречаются параллелепипеды, у которых стороны имеют разную длину. В таком случае, для подсчета суммы длин ребер параллелепипеда нужно учесть все ребра фигуры.
Для параллелепипеда со сторонами разной длины общая формула для подсчета суммы длин ребер будет следующей:
- Сумма длин всех ребер = 2 * (a + b + c), где a, b и c – длины сторон параллелепипеда.
Таким образом, чтобы вычислить сумму длин ребер параллелепипеда со сторонами разной длины, нужно сложить длины всех его ребер по формуле 2 * (a + b + c), где a, b и c – длины сторон.
Зная данную формулу, можно легко рассчитать сумму длин ребер параллелепипеда со сторонами разной длины и использовать это значение в дальнейших вычислениях или задачах, связанных с этой геометрической фигурой.
Правильный параллелепипед с равными и одинаково расположенными гранями
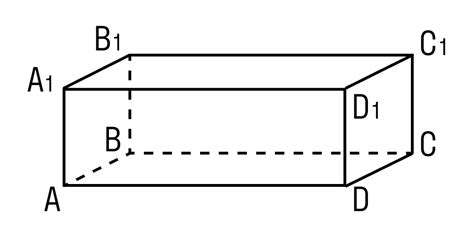
Чтобы визуализировать правильный параллелепипед, можно представить его в виде куба, так как все его ребра равны друг другу. Поэтому при изучении методов подсчета суммы длин ребер куба можно применять и к правильному параллелепипеду.
Для правильного параллелепипеда с равными и одинаково расположенными гранями можно использовать методы подсчета суммы длин ребер куба. Например, можно вычислить сумму длин всех ребер, используя формулу L = 12a, где L – сумма длин ребер, а – длина одного ребра.
Также можно использовать метод подсчета суммы длин ребер по формуле L = 4l + 4w + 4h, где l – длина, w – ширина и h – высота параллелепипеда. При этом необходимо помнить, что для правильного параллелепипеда все грани равны между собой, а углы между ребрами равны 90 градусам.
Таким образом, правильный параллелепипед с равными и одинаково расположенными гранями является геометрической фигурой, у которой можно применять методы подсчета суммы длин ребер куба. Это позволяет упростить вычисления и получить точные результаты.
Неправильный параллелепипед с неравными сторонами и неравномерно расположенными гранями
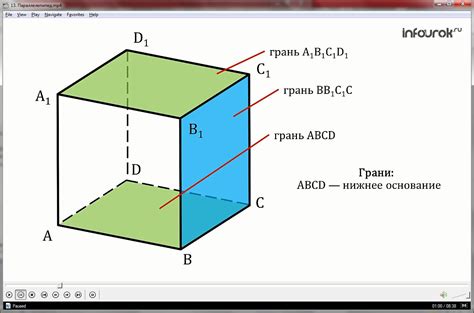
Неправильный параллелепипед с неравными сторонами и неравномерно расположенными гранями является сложной геометрической формой. Его грани могут быть неодинаковыми и не находиться на одинаковом расстоянии друг от друга. Это создает сложности в расчете площади поверхности и подсчете суммы длин ребер.
Для решения задачи подсчета суммы длин ребер неправильного параллелепипеда требуется изучение геометрических свойств такой фигуры. Важно определить длины всех ребер и применить соответствующие методы подсчета.
Таблица может быть использована для удобной организации информации о ребрах неправильного параллелепипеда. В таблице можно указать длины ребер и их нумерацию для последующего подсчета суммы.
| Ребро | Длина |
|---|---|
| Ребро 1 | 7 см |
| Ребро 2 | 9 см |
| Ребро 3 | 5 см |
| Ребро 4 | 8 см |
| Ребро 5 | 6 см |
| Ребро 6 | 4 см |
Сумма длин ребер рассчитывается путем сложения длин всех ребер. В данном случае, сумма длин ребер неправильного параллелепипеда будет равна 39 см (7 + 9 + 5 + 8 + 6 + 4).
Изучение и анализ неправильного параллелепипеда с неравными сторонами и неравномерно расположенными гранями помогают углубить понимание геометрических особенностей такой фигуры и применить соответствующие методы подсчета. Это важные навыки, которые могут быть применены в более сложных геометрических задачах и решениях.
Как учесть радиус скругленных углов куба или параллелепипеда

Если на кубе или параллелепипеде выполнено скругление углов на всех гранях, то необходимо прибавить к сумме длин ребер периметр каждого скругленного угла. Для куба это будет величина, равная 8 разам радиусу скругленного угла, а для параллелепипеда - 12 разам радиусу.
Если скругление углов выполнено только на нескольких гранях, то к сумме длин ребер нужно прибавить периметр скругленного угла каждой грани, на которой есть скругление. В этом случае каждая грань будет вносить свой вклад в сумму длин ребер.
В случае, если скругление выполнено только на одной или нескольких гранях, но не на всех, подсчет длин ребер становится более сложным. В таких ситуациях нужно учитывать не только периметр каждого скругленного угла, но и длины ребер, которые соединяют грани со скругленными углами.
Важно отметить, что при подсчете суммы длин ребер необходимо учесть не только скругленные углы, но и прямые углы, если они присутствуют. Все углы, включая скругленные и прямые, считаются при подсчете длин ребер.
Таким образом, для точного подсчета суммы длин ребер куба или параллелепипеда необходимо учесть радиус скругленных углов и взаимное соединение граней. Это позволит получить более точный результат в зависимости от того, на скольких гранях выполнено скругление углов.
Методы подсчета длины ребер в программе для вычислений
Для проведения вычислений и определения длины ребер куба и параллелепипеда в программе необходимо использовать соответствующие методы.
Для куба можно использовать следующий метод:
- Вычислить длину ребра куба, используя формулу 6 * a, где a - длина одной из сторон куба.
Для параллелепипеда можно использовать следующие методы:
- Вычислить длину ребра, соединяющего две вершины параллелепипеда, используя формулу sqrt(a^2 + b^2 + c^2), где a, b, и c - длины трех сторон параллелепипеда.
- Вычислить длины ребер параллелепипеда, используя формулы 2 * (a + b), 2 * (a + c) и 2 * (b + c), где a, b и c - длины трех сторон параллелепипеда.
Выбор метода подсчета длины ребер зависит от поставленной задачи и доступных данных.