Период колебаний математического маятника - это временной интервал, за который маятник проходит полный цикл колебаний - от точки максимального отклонения в одну сторону до точки максимального отклонения в другую сторону и обратно. Длина маятника является основным фактором, который влияет на его период колебаний.
Согласно формуле периода колебаний, период обратно пропорционален корню квадратному из длины маятника. То есть, с увеличением длины маятника, период его колебаний увеличивается. Это означает, что маятник с более длинной нитью будет выполнять медленные колебания в сравнении с маятником с более короткой нитью.
Для лучшего понимания этого явления, можно провести простой эксперимент. Возьмите две нити одинаковой массы и подвесьте на них два разных маятника. Один маятник с короткой нитью, другой - с более длинной. Запустите оба маятника одновременно и наблюдайте. Вы увидите, что маятник с более длинной нитью будет занимать больше времени для совершения полного цикла колебаний по сравнению с маятником с короткой нитью.
Это связано с тем, что маятники с разной длиной нити имеют разную физическую характеристику, а именно - разную гравитационную потенциальную энергию при отклонении. С увеличением длины нити, маятник обладает более высокой потенциальной энергией, что требует больше времени для его перехода из одной крайней точки в другую.
Математический маятник: период колебаний и его зависимость от длины
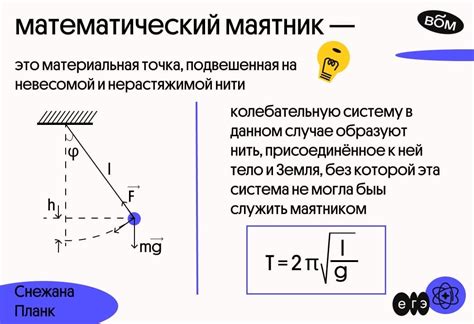
Оказывается, период колебаний математического маятника зависит от его длины. Для маятников одинаковой массы, период колебаний будет увеличиваться с увеличением длины маятника. Это связано с тем, что чем длиннее маятник, тем больше времени ему требуется для прохождения полного колебания.
Существует формула, которая позволяет вычислить период колебаний математического маятника:
- Период колебаний (T) равен удвоенному пи (π) умноженному на квадратный корень из отношения длины маятника (L) к ускорению свободного падения (g):
T = 2π√(L/g)
Из этой формулы видно, что с увеличением длины маятника (L), период колебаний (T) также увеличивается. Это может быть проиллюстрировано следующим образом:
- Представим два математических маятника одинаковой массы, но с разными длинами: один маятник имеет длину L1, а другой - L2 (L2 > L1).
- Если у нас есть возможность измерить примерно одновременный период колебаний обоих маятников, то мы обнаружим, что период колебаний маятника с большей длиной (L2) будет дольше, чем у маятника с меньшей длиной (L1).
Первоначальные предположения

Для изучения изменения периода колебаний математического маятника с увеличением длины требуется установить некоторые первоначальные предположения.
- Математический маятник представляет собой идеализированную систему, состоящую из точечной массы, подвешенной на невесомом и нерастяжимом нитевидном подвесе.
- Маятник свободно колеблется в одной плоскости без каких-либо внешних воздействий.
- Изначально маятник находится в положении равновесия, т.е. статического состояния без колебаний.
- Начальное отклонение маятника происходит по вертикали и влияет на его период.
- Масса маятника предполагается константной во время всех колебаний.
- Медленные колебания маятника предполагают, что сопротивление воздуха и другие неидеальные факторы не оказывают значительного влияния на результаты.
Учитывая данные предположения, можно приступить к анализу влияния длины маятника на его период колебаний.
Внимание на длину маятника
Длина маятника определяет его период колебаний по формуле:
T = 2π√(l/g)
Где T - период колебаний, l - длина маятника, g - ускорение свободного падения.
Увеличение длины маятника приводит к увеличению его периода колебаний. Это означает, что маятник будет колебаться медленнее и занимать больше времени на один цикл колебаний. Такая зависимость является прямой: с увеличением длины маятника, его период колебаний будет увеличиваться пропорционально.
Изучение этой зависимости позволяет управлять периодом колебаний маятника путем изменения его длины. Это может быть полезно, например, при создании точных часов или при проектировании маятниковых механизмов. Знание зависимости периода колебаний от длины маятника позволяет инженерам подобрать оптимальные параметры для заданного применения.
Исследование длины маятника имеет большое значение не только в физике и инженерии, но и в других областях науки и техники. Это позволяет понять особенности колебательных систем, а также использовать их в различных практических приложениях.
Формула периода колебаний и длина маятника
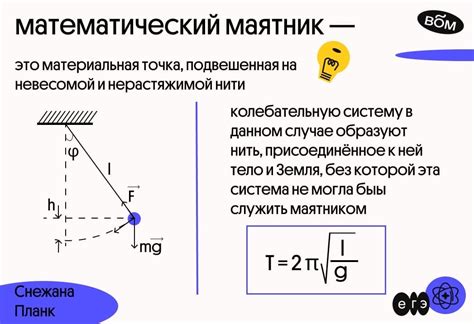
Формула периода колебаний для математического маятника выглядит следующим образом:
| Т | = | 2π | √ | (L / g) |
Где:
- Т - период колебаний;
- π - математическая константа, примерное значение 3,14159 ...;
- L - длина маятника;
- g - ускорение свободного падения, примерное значение 9,8 м/с².
Из формулы видно, что период колебаний математического маятника прямо пропорционален квадратному корню из длины маятника. То есть, при увеличении длины маятника, период колебаний также увеличивается.
Эту зависимость можно интерпретировать следующим образом: чем длиннее маятник, тем больше время требуется для того, чтобы он совершил одно полное колебание.
Важно отметить, что формула периода колебаний справедлива для малых амплитуд колебаний, когда угол отклонения маятника мал. При больших амплитудах колебаний формула может не давать точного значения периода.
Практическое применение

Изучение изменения периода колебаний математического маятника с увеличением его длины имеет широкое практическое применение в различных областях науки и техники. Вот несколько сфер, где эти знания могут быть полезны:
| Область | Практическое применение |
|---|---|
| Физика | Расчет периодов колебаний маятников используется для измерения времени и проведения точных физических экспериментов. Например, в серийных часах используются математические маятники, у которых длина задается таким образом, чтобы период колебаний был равен одной секунде. |
| Архитектура | Знание зависимости периода колебаний от длины маятника может быть использовано для определения оптимальных параметров подвески светильников, каминов и других элементов интерьера, чтобы обеспечить их стабильность и избежать нежелательных колебаний. |
| Инженерия | В промышленности и при проектировании сооружений знание законов колебаний может быть использовано для предотвращения резонансных явлений, которые могут привести к разрушению конструкций. Например, вибрации мостов или зданий можно контролировать, изменяя параметры системы, включая длину маятника. |
| Астрономия | Изучение математического маятника помогает астрономам контролировать точность и стабильность измерений в телескопах и других приборах, используемых для изучения космоса. Знание периода колебаний может быть использовано для коррекции ошибок и повышения точности наблюдений. |
Таким образом, понимание изменения периода колебаний математического маятника с увеличением его длины имеет широкое практическое применение в различных научных и технических областях, способствуя улучшению и оптимизации многих процессов и явлений.