Равнобедренная трапеция – это геометрическая фигура, у которой две противоположные стороны равны между собой, а две другие стороны – неравны. В такой фигуре особое внимание обращают на свойства диагоналей. У равнобедренной трапеции есть две диагонали: большая и меньшая. Интересно, как связаны между собой эти диагонали и как они изменяются при изменении сторон трапеции?
Для начала, стоит отметить, что длина диагонали трапеции может быть выражена через длины её сторон и основания. Если обозначить основания трапеции как a и b, то длину диагонали можно вычислить по формуле:
d = √(a^2 + b^2 + 2ab * cos(θ))
Таким образом, диагонали равнобедренной трапеции зависят от длин её сторон и угла наклона трапеции.
Зависимость длин диагоналей в равнобедренной трапеции
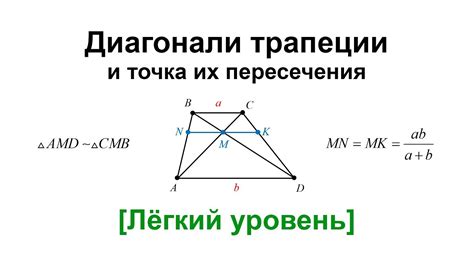
Длина главной диагонали (пересекающей ось симметрии и соединяющей вершины с разными основаниями) в равнобедренной трапеции может быть вычислена по следующей формуле:
Длина главной диагонали = √(сторона1^2 + сторона2^2 - 2 * сторона1 * сторона2 * cos(угол между основаниями))
Для вычисления длины побочной диагонали (параллельной оси симметрии и соединяющей середины боковых сторон) применяется следующая формула:
Длина побочной диагонали = √(основание1^2 + основание2^2 + 2 * основание1 * основание2 * cos(угол между основаниями))
Из этих формул видно, что длина диагоналей зависит от сторон равнобедренной трапеции и угла между ее основаниями. При увеличении сторон или изменении угла между основаниями, длины диагоналей также изменяются. Отношение длин диагоналей в равнобедренной трапеции может быть использовано для решения различных геометрических задач и нахождения неизвестных величин.
Соотношение диагоналей в равнобедренной трапеции
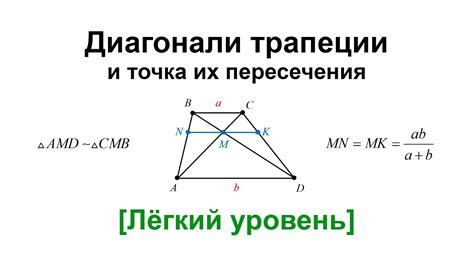
Главная диагональ - это отрезок, соединяющий две вершины, которые не принадлежат одной параллельной стороне. Побочная диагональ - это отрезок, соединяющий середины боковых сторон трапеции.
Соотношение диагоналей в равнобедренной трапеции может быть представлено следующим образом:
| Главная диагональ | Побочная диагональ |
| Внутри треугольника | Внутри треугольника |
| Расстояние между основаниями | Высота трапеции |
Однако, соотношение диагоналей зависит от угла при вершине равнобедренной трапеции. Если угол равен 90 градусам, то главная диагональ будет равна сумме оснований, а побочная диагональ равна высоте. Если угол меньше 90 градусов, то главная диагональ будет меньше суммы оснований, а побочная диагональ будет меньше высоты. Если угол больше 90 градусов, то главная диагональ будет больше суммы оснований, а побочная диагональ будет больше высоты.
Таким образом, в равнобедренной треугольнике соотношение диагоналей зависит от угла при вершине и может быть различным. Но всегда можно установить соотношение между диагоналями и основаниями или высотой трапеции.
Изменение диагоналей при изменении сторон трапеции
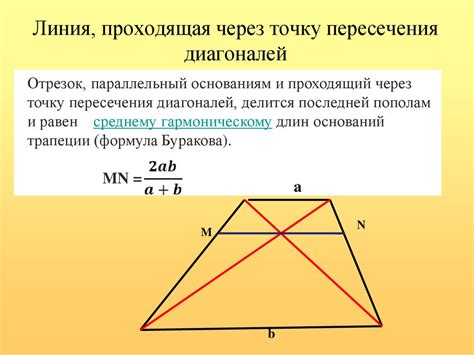
Когда меняются стороны равнобедренной трапеции, длины ее диагоналей также изменяются. При увеличении длины оснований трапеции диагональ, соединяющая эти основания, становится длиннее. Это происходит потому, что при увеличении оснований углы между ними становятся более тупыми, и диагональ становится больше по теореме косинусов.
С другой стороны, диагональ, соединяющая более короткие боковые стороны трапеции, также меняется при изменении сторон. При увеличении длины боковых сторон диагональ становится короче, так как угол между боковой стороной и одним из оснований становится меньше.
Таким образом, изменение сторон равнобедренной трапеции приводит к изменению длин ее диагоналей. Длина диагонали, соединяющей основания, увеличивается при увеличении оснований, а длина диагонали, соединяющей боковые стороны, уменьшается при увеличении боковых сторон.
| Основания трапеции | Диагональ, соединяющая основания | Диагональ, соединяющая боковые стороны |
|---|---|---|
| Увеличение | Увеличение | Уменьшение |
| Уменьшение | Уменьшение | Увеличение |



