Геометрические фигуры - одна из основных тем в изучении математики. Они помогают нам понять и описать мир вокруг нас, будь то натуральные объекты или абстрактные идеи. Но когда и кому пришла в голову идея разбивать пространство на такие простые формы?
История геометрии уходит своими корнями в глубину веков. Однако, даже в древние времена люди были заинтересованы не только во внешнем мире, но и в его устройстве. Именно в этот момент они начинали задавать себе вопросы о форме объектов и их свойствах. И так появились первые представители древней геометрии.
Одним из величайших геометров древности считается Евклид. Он родился около 300 года до нашей эры и создал знаменитый труд "Начала". Эта книга стала основой для изучения геометрии на протяжении многих веков. Евклид разработал ряд аксиом и постулатов, которые приняты до сих пор и лежат в основе геометрии.
Геометрические фигуры: их происхождение и развитие
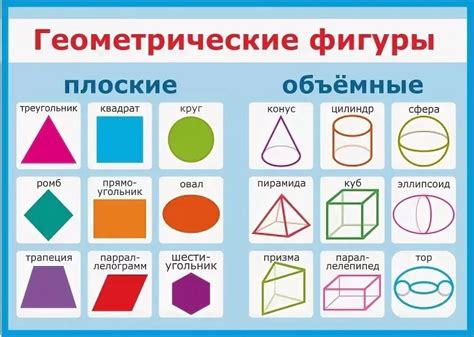
Вопрос о том, когда и кто придумал геометрические фигуры, остается открытым, так как основы геометрии были изучены еще в древности. Однако, первые известные записи о геометрических фигурах появились в Египте около 3000 года до нашей эры.
Египтяне использовали геометрические фигуры для измерения земли и строительства пирамид. Они были первыми, кто обратил внимание на свойства и отношения между фигурами, такими как треугольники и прямоугольники.
В Древней Греции геометрия пережила настоящий расцвет. Великий греческий математик Евклид в своем труде "Начала" описал основные принципы геометрии и предложил систематический подход к изучению фигур и их свойств.
С тех пор геометрия продолжила свое развитие и стала одной из важнейших областей математики. Были открыты новые фигуры и формулированы сложные теоремы. Сегодня геометрия является неотъемлемой частью образования и научных исследований.
Геометрические фигуры удивительны своей симметрией и простотой, но при этом являются основой для понимания и изучения сложных форм и структур. Их происхождение и развитие являются важными аспектами нашего культурного наследия и научного прогресса.
Геометрические фигуры в Древнем Египте

Древний Египет, одна из старейших цивилизаций мира, имела свою собственную систему геометрических фигур, на основе которой строились многочисленные архитектурные и инженерные сооружения.
Одной из основных геометрических фигур, используемых в Древнем Египте, был треугольник. Он играл важную роль в строительстве пирамид, так как являлся основой для расчета углов и сторон пирамидальных структур. Древние египтяне великие астрономы и математики, внимательно изучали звезды и небосвод, поэтому использовали треугольники для расчета расстояний и определения направления.
Еще одной важной геометрической фигурой, широко применявшейся в Древнем Египте, был квадрат. Квадраты строились в качестве основы для построения стен и сооружений. Использование квадратов позволяло обеспечить стабильность и прочность конструкций.
Помимо треугольника и квадрата, в Древнем Египте использовались также прямоугольники, круги и овалы. По форме они в большинстве своем повторяли естественные образования природы, такие как реки и озера.
- Треугольник - основа для расчета углов и сторон пирамид.
- Квадрат - основа для построения стен и сооружений.
- Прямоугольник - использовался для создания различных архитектурных элементов.
- Круг и овал - повторяли форму природных образований.
Использование геометрических форм позволяло египтянам создавать прочные и устойчивые конструкции, а также внушать ощущение гармонии и равновесия. Кроме того, геометрические фигуры имели символическое значение и были связаны с мифологией и религией Древнего Египта.
Геометрия в Древней Греции

Древняя Греция считается колыбелью геометрии, так как именно здесь были заложены основы этой науки.
Заслугу в развитии геометрии в Древней Греции принадлежит великому математику Евклиду, жившему в IV веке до нашей эры. Он написал знаменитую книгу "Начала", в которой изложил основные понятия и теоремы геометрии. Это произведение является одним из основных источников знаний по геометрии до настоящего времени.
Главным понятием, разработанным Евклидом, были аксиомы - неразрушаемые утверждения, которые он использовал в своих доказательствах. Его система аксиом получила название евклидовой геометрии и является основой классической геометрии.
Греки также внесли вклад в развитие других геометрических фигур. Например, Пифагор и его ученики изучали прямоугольные треугольники и сформулировали известную теорему Пифагора. Они открыли, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Также стоит отметить Аполлония Пергский, который разработал теорию конических сечений. Он изучал различные фигуры, возникающие при пересечении конуса и плоскости. Его работа легла в основу современной алгебраической геометрии.
Геометрия в Древней Греции имела огромное значение и представляла собой одну из важнейших наук того времени. Её развитие послужило фундаментом для всех последующих достижений в этой области знаний.
Влияние Востока на развитие геометрии

История геометрии, как науки, насчитывает тысячелетия. Но мало кто знает, что основы геометрических знаний были заложены именно на Востоке, в древних цивилизациях Месопотамии и Египта.
Восточные математики и ученые сделали значительные вклады в развитие геометрии. Благодаря им,были открыты основные геометрические фигуры, такие как круг, треугольник, квадрат, прямоугольник и другие.
Одним из важнейших открытий в геометрии благодаря Востоку была система координат, позволяющая описывать точки в пространстве. Это стало основой для развития аналитической геометрии, которая позволяет изучать геометрические объекты с помощью алгебраических методов.
Восток также способствовал развитию геометрии через изучение и применение геометрических конструкций и построений. Строительство великолепных дворцов и храмов требовало навыков геометров для создания симметричных и гармоничных форм.
Восточные ученые, такие как Пифагор, Евклид и Архимед, продолжали развивать геометрию, но их основы были заложены благодаря работам древних восточных математиков. До сих пор многие принципы геометрии остаются актуальными и используются в различных областях знаний и наук.
Геометрия в средние века

В средние века геометрия окончательно стала отдельной наукой и получила огромное развитие. Геометрические знания глубоко проникли в жизнь средневекового общества, в особенности в архитектуру и строительство соборов и замков.
Важным вкладом в развитие геометрии были работы арабских математиков, которые хранительницей античного наследия стала Испания.
Одним из наиболее известных средневековых геометров стал арабский математик Аль-Хорезми, автор монументального труда "Алгебра и альмукабала". Его работы содержали многочисленные задачи и примеры, решение которых требовало применения геометрических методов и инструментов.
В архитектуре средневековья геометрия применялась для создания сложных и инновационных архитектурных форм. Например, соборы в готическом стиле, такие как Нотр-Дам или Йоркский собор, великолепно иллюстрируют геометрические принципы и симметрию.
Геометрия в средние века играла не только роль практической науки, но и имела свою философскую и символическую сторону. Геометрические формы и символы использовались для выражения религиозных или философских идей. Они служили способом визуализации и передачи сложных концепций.
| Автор | Годы жизни | Вклад в геометрию |
|---|---|---|
| Аль-Хорезми | 780-850 | Автор "Алгебры и альмукабалы" |
| Эвклид | ок. 300-275 до н.э. | Автор "Начал геометрии" |
| Пифагор | ок. 570-495 до н.э. | Развитие пифагорейской школы, внесение вклада в геометрию |
Роль геометрии в ренессансе

В эпоху Возрождения геометрия играла неотъемлемую роль в различных сферах искусства и научных исследований. Геометрические фигуры и принципы были важными инструментами для архитекторов, скульпторов, живописцев и ученых.
Архитекторы использовали геометрию для создания гармоничных и пропорциональных зданий. Они применяли различные геометрические формы, такие как круги, квадраты и треугольники, чтобы достичь симметрии и баланса в архитектурных композициях.
Скульпторы также полагались на геометрию при создании своих произведений. Они использовали геометрические формы для определения пропорций тела и поз, а также при моделировании и создании структур и деталей скульптур.
Живопись Возрождения также необходили геометрические принципы. Художники использовали перспективу, которая основана на геометрии, чтобы создавать иллюзию трехмерности на плоскости холста. Они также использовали пропорции и геометрические формы для создания гармоничных композиций и ритмичных аранжировок.
Геометрия имела важное значение и в научных исследованиях эпохи. Исследователи и ученые использовали геометрию для изучения физических явлений и разработки новых теорий. Например, известный ученый и художник Леонардо да Винчи использовал геометрию в своих исследованиях анатомии и физики.
В целом, геометрия в ренессансе играла роль инструмента, с помощью которого мастера и ученые достигали гармонии, пропорции, симметрии и красоты в своих работах и открытиях. Она позволяла им совершенствоваться в искусстве и науке, и стала неотъемлемой частью этого периода.
Современная геометрия и ее приложения

В современной геометрии активно используются математические методы и инструменты, такие как алгебра, топология и аналитическая геометрия. Это позволяет решать сложные задачи, связанные с пространством и формой объектов.
Современная геометрия имеет множество приложений в различных областях науки и техники. Она используется в компьютерной графике и визуализации, в теории кодирования и криптографии, в робототехнике и автоматическом управлении. Геометрические принципы применяются в архитектуре и дизайне, в оптике и физике, в медицине и биологии.
Одно из самых известных приложений современной геометрии - компьютерная графика. С ее помощью создаются реалистичные трехмерные модели объектов и виртуальные миры. Геометрические алгоритмы используются для решения задач освещения, текстурирования и анимации.
Современная геометрия непрерывно развивается и находит все новые приложения. Изучение ее основ помогает развивать логическое мышление и абстрактное мышление, а также находить решения для различных проблем в разных областях.