Упругость - одно из важнейших свойств материалов, определяющее их способность вернуться в исходное состояние после деформации. Сила упругости позволяет материалам сопротивляться внешним нагрузкам и сохранять свою форму. Как изменится сила упругости при увеличении удлинения в 3 раза - интересный вопрос, требующий внимательного изучения.
Для начала, необходимо понять, что сила упругости связана с законом Гука, который описывает зависимость силы деформации от удлинения материала. Согласно этому закону, сила упругости пропорциональна удлинению материала.
Если удлинение увеличивается в 3 раза, то сила упругости также изменится. В этом случае, можно ли сказать, что она увеличится в 3 раза? Ответ на этот вопрос зависит от свойств конкретного материала.
Некоторые материалы обладают линейной пропорциональностью силы упругости и удлинения, при которой увеличение удлинения в 3 раза действительно приведет к увеличению силы в 3 раза. Однако, существуют и другие материалы с нелинейной зависимостью силы упругости от удлинения. В этом случае, изменение силы упругости может быть не таким простым.
Изменение силы упругости
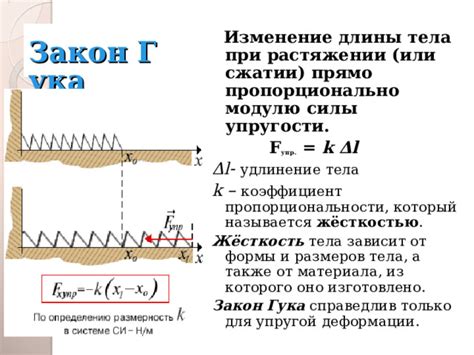
Упругий материал обладает свойством возвращать свою форму и размеры после прекращения воздействия внешней силы. Сила упругости определяется по закону Гука и зависит от удлинения пружины и жесткости материала.
Если удлинение пружины увеличивается в 3 раза, то сила упругости также изменится. По закону Гука, сила упругости пропорциональна удлинению и обратно пропорциональна коэффициенту жесткости. Таким образом, при увеличении удлинения в 3 раза, сила упругости возрастет в 3 раза.
Это означает, что упругий материал станет более сжимаемым и будет оказывать большую силу против деформации. Изменение силы упругости может быть важным фактором при различных инженерных расчетах и конструкциях, где упругость материала играет роль.
Что такое упругость и ее сила
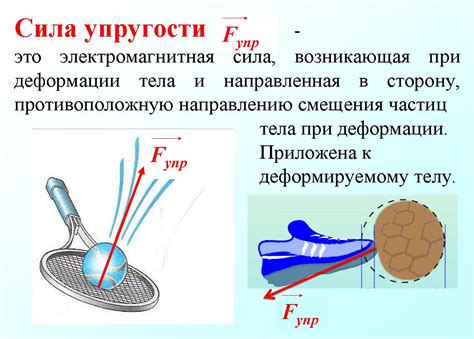
Сила упругости – это сила, которая возникает при изменении формы или размера материала и направлена против этого изменения.
Сила упругости пропорциональна удлинению или сжатию материала. То есть, при увеличении удлинения, сила упругости также будет увеличиваться.
Если удлинение материала увеличивается в 3 раза, то сила упругости также увеличится в 3 раза. Это связано с тем, что сила упругости прямо пропорциональна удлинению материала.
Например, если при удлинении материала на 1 сантиметр сила упругости составляет 10 Н, то при удлинении в 3 раза (то есть на 3 сантиметра) сила упругости будет составлять 30 Н.
Сила упругости важна при расчете и проектировании различных конструкций, чтобы учесть воздействие деформаций и предотвратить разрушение материала.
Влияние удлинения на силу упругости
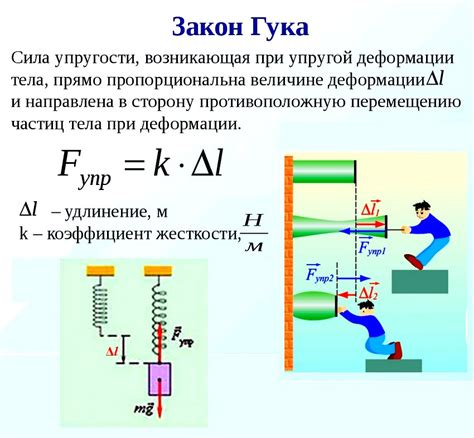
Удлинение материала является одним из способов деформации, при котором происходит изменение его формы под воздействием внешних сил. Удлинение может быть вызвано различными факторами, такими как нагрузка, изменение температуры или давление.
При увеличении удлинения в 3 раза, сила упругости также будет изменяться. В зависимости от типа материала и его свойств, величина силы упругости может либо увеличиваться, либо оставаться постоянной, либо уменьшаться.
Для некоторых материалов, таких как идеально упругие или "жесткие" твердые тела, сила упругости прямо пропорциональна удлинению. То есть, если удлинение увеличивается в 3 раза, то сила упругости также увеличивается в 3 раза.
Однако для других материалов, таких как вязкие жидкости или деформируемые тела, величина силы упругости может меняться нелинейно с удлинением. В этом случае, при увеличении удлинения в 3 раза, сила упругости может либо увеличиваться, либо уменьшаться, в зависимости от специфических свойств материала.
В таблице ниже приведены примеры изменений силы упругости при увеличении удлинения в 3 раза для различных типов материалов:
| Тип материала | Изменение силы упругости |
|---|---|
| Идеально упругий (жесткий) твердый материал | Увеличение в 3 раза |
| Вязкая жидкость | Нелинейное изменение |
| Деформируемое тело | Нелинейное изменение |
Таким образом, при увеличении удлинения в 3 раза, сила упругости может меняться по-разному в зависимости от типа материала. Понимание этого взаимосвязанного процесса является важным аспектом в изучении и применении упругих материалов в различных областях науки и техники.
Увеличение удлинения в 3 раза

Сила упругости определяется законом Гука: F = k * ΔL, где F - сила упругости, k - коэффициент жёсткости пружины и ΔL - удлинение. Таким образом, сила упругости прямо пропорциональна удлинению.
При увеличении удлинения в 3 раза, сила упругости также увеличится в 3 раза. Это связано с прямой пропорциональностью между силой упругости и удлинением, которая имеет место при выполнении закона Гука.
Изменение силы упругости при увеличении удлинения в 3 раза влияет на поведение упругого тела. Увеличение удлинения может привести к большим деформациям и изменению формы тела под действием силы. Такие изменения могут быть важными для понимания свойств материалов и их использования в различных областях, таких как строительство, авиация и машиностроение.
Важно отметить, что сила упругости может достигать пределов прочности материала. При превышении этих пределов, материал может потерять свою упругую способность и деформироваться необратимо. Таким образом, важно учитывать и контролировать удлинение и силу упругости при разработке и использовании объектов, испытывающих воздействие силы.
Изменение силы упругости при увеличении удлинения в 3 раза

Чтобы понять, как изменится сила упругости, нужно обратиться к закону Гука. Закон Гука устанавливает прямую пропорциональность между силой упругости и удлинением упругого тела:
F = k * Δl
где F – сила упругости, k – коэффициент упругости, Δl – удлинение.
Если удлинение увеличивается в 3 раза, то Δl становится равным 3Δl. Подставив это значение в формулу закона Гука, получим:
F = k * 3Δl
Учитывая, что 3Δl = 3 * Δl, можно упростить выражение:
F = 3 * k * Δl
Таким образом, если удлинение увеличивается в 3 раза, сила упругости также увеличивается в 3 раза. Это говорит о том, что сила упругости и удлинение пропорциональны друг другу.
Изменение силы упругости при увеличении удлинения в 3 раза имеет физическую практическую значимость. Знание этого закона помогает инженерам и конструкторам предсказывать поведение упругих материалов и строить их таким образом, чтобы справиться с большими нагрузками и деформациями.