Факториал - это одно из основных понятий математики, которое находит широкое применение в программировании. В данной статье мы рассмотрим, как работает факториал в языке программирования Паскаль и как его можно использовать в различных задачах.
Факториал числа - это произведение всех натуральных чисел от 1 до данного числа. Обозначается факториал числа "n" как "n!". Например, факториал числа 5 (обозначается как 5!) равен 5 * 4 * 3 * 2 * 1 = 120.
В языке программирования Паскаль вычисление факториала реализуется с помощью цикла или рекурсии. При использовании цикла, переменная увеличивается от 1 до заданного числа, и на каждой итерации производится умножение предыдущего значения на текущую переменную. При использовании рекурсии, функция вызывает саму себя с уменьшенным аргументом, и результат умножается на текущую переменную.
Факториалы широко применяются в математике, физике и других науках для решения различных задач. Например, они используются в комбинаторике для подсчета комбинаций и перестановок, а также в теории вероятностей для вычисления факториальных коэффициентов. В программировании факториалы часто используются для решения задач с большим объемом вычислений или для оптимизации кода.
Что такое факториал в Паскале

Например, факториал числа 5 (обозначается как 5!) равен произведению всех натуральных чисел от 1 до 5:
5! = 5 * 4 * 3 * 2 * 1 = 120.
Факториалы широко применяются в комбинаторике и математическом анализе. Они используются для решения задач, связанных с различными комбинаторными структурами, перестановками элементов и вычислением вероятностей.
Паскаль предоставляет удобные инструменты для вычисления факториала. С помощью циклов, рекурсии и математических операций можно реализовать алгоритмы для расчета факториала числа любой величины. Это позволяет упростить и автоматизировать работу с факториалами в программировании и научных расчетах.
Принцип работы факториала в Паскале
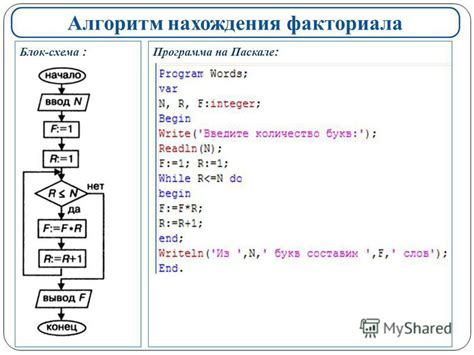
В Паскале существует несколько способов реализации функции, вычисляющей факториал. Один из наиболее популярных способов - использование рекурсии.
Рекурсивная реализация факториала заключается в том, что функция вызывает саму себя с аргументом, уменьшенным на 1, до тех пор пока аргумент не станет равным 1. Затем, функция возвращает результат, умноженный на текущий аргумент.
Например, для вычисления факториала числа 5 с использованием рекурсии в Паскале:
- Вызываем функцию с аргументом 5
- Функция вызывает саму себя с аргументом 4
- Функция вызывает саму себя с аргументом 3
- Функция вызывает саму себя с аргументом 2
- Функция вызывает саму себя с аргументом 1
- Аргумент становится равным 1, функция возвращает 1
- Функция возвращает результат (1) умноженный на текущий аргумент (2) = 2
- Функция возвращает результат (2) умноженный на текущий аргумент (3) = 6
- Функция возвращает результат (6) умноженный на текущий аргумент (4) = 24
- Функция возвращает результат (24) умноженный на текущий аргумент (5) = 120
Таким образом, факториал числа 5 равен 120.
Рекурсивная реализация позволяет легко вычислять факториал любого положительного целого числа, но может занимать больше времени и ресурсов при больших значениях числа, так как функция вызывается многократно.
Кроме рекурсивной реализации, существуют и итеративные способы вычисления факториала в Паскале, которые не используют рекурсию и могут быть более эффективными при работе с большими значениями числа.
Примеры использования факториала в Паскале

1. Вычисление комбинаторных коэффициентов: Комбинаторные коэффициенты используются для подсчета количества возможных комбинаций, которые могут быть созданы из некоторого набора элементов. Факториал часто используется для вычисления комбинаторных коэффициентов, таких как биномиальные коэффициенты. Например, можно использовать факториал для вычисления чисел из последовательности Паскаля.
2. Вычисление вероятности событий: Факториал может использоваться для вычисления вероятности событий в комбинаторных задачах. Например, если у вас есть набор N элементов, и вы хотите узнать, сколько различных способов можно выбрать K элементов из этого набора, то факториал может помочь вам подсчитать количество этих способов.
3. Решение задач каталексиса: Каталексис - это понятие в комбинаторике, которое описывает количество способов разбиения группы объектов на непересекающиеся блоки. Факториал может быть использован для решения задач каталексиса, где необходимо определить количество различных способов разбиения набора элементов.
4. Подсчет перестановок: Факториал может быть использован для подсчета числа перестановок, которые могут быть созданы из некоторого набора элементов. Например, если у вас есть набор из N элементов, факториал может помочь вам вычислить количество различных перестановок этих элементов.
Все эти примеры демонстрируют широкий спектр применений факториала в математике и комбинаторике. В Паскале факториал может быть реализован с помощью рекурсивной функции или с использованием циклов.
Как вычислить факториал в Паскале

Вариант с использованием цикла:
function factorial(n:integer):integer;
var
i, result: integer;
begin
result := 1;
for i := 2 to n do
result := result * i;
factorial := result;
end;
В этой функции мы используем цикл, начиная с числа 2 и выполняя умножение каждого числа от 2 до данного числа на результат. Итоговое значение сохраняется в переменной result и возвращается в качестве результата функции.
Вариант с использованием рекурсии:
function factorial(n:integer):integer;
begin
if n = 0 then
factorial := 1
else
factorial := n * factorial(n - 1);
end;
В этой функции мы используем рекурсию, вызывая функцию саму себя с уменьшенным на единицу аргументом. Рекурсивный вызов прекращается, когда аргумент становится равным нулю, и возвращается 1. Иначе, происходит умножение текущего числа на результат рекурсивного вызова функции, которое и становится результатом функции.
Оба варианта позволяют вычислить факториал числа в Паскале. Выбор между ними зависит от предпочтений программиста и требований конкретной задачи.
Метод рекурсии для вычисления факториала

Для вычисления факториала числа n с помощью рекурсии, функция будет вызывать себя с аргументом на единицу меньше текущего значения до тех пор, пока не достигнет базового случая, когда аргумент станет равным 0 или 1.
Например, рекурсивная функция для вычисления факториала может выглядеть следующим образом:
function factorial(n) {
if (n === 0