Математика и искусство давно испытывают взаимное влияние, и одной из областей, где математические концепции находят свое уникальное применение, является рисование. Понимание математических принципов позволяет художникам создавать удивительные и отличные от реальности произведения искусства.
Изучение трюков и методов математического рисования позволяет освоить эффективные инструменты, которые помогут в создании сложных и захватывающих композиций. Независимо от того, являетесь ли вы художником или любителем, познание этих методов поможет вам расширить свой художественный кругозор и добавить новые техники в свой арсенал.
Используют ли художники математику в своей работе?
Многие известные художники использовали и используют математические концепции в своих работах. Леонардо да Винчи, например, применял пропорции Золотого сечения при создании своих произведений искусства. Эта математическая концепция позволяет добиться гармоничных и привлекательных пропорций в любом изображении. Кроме того, художники также часто используют геометрические формы и фигуры, чтобы создать сбалансированные и эстетически привлекательные композиции.
В этой статье мы познакомимся с некоторыми из трюков и методов математического рисования, которые вы можете использовать, чтобы создать уникальные и красивые произведения искусства. От изучения фракталов и перспективы до применения математических пропорций и логики в цветовой гамме, вы обнаружите, что мир математического рисования настолько же увлекателен и разнообразен, как и само искусство.
Трюки и методы математического рисования

1. Использование тригонометрических функций
Одним из основных инструментов математического рисования являются тригонометрические функции, такие как синус и косинус. Используя эти функции, можно легко создавать красивые геометрические фигуры. Например, чтобы нарисовать круг, можно использовать параметрические уравнения:
x = r * cos(t)
y = r * sin(t)
где r - радиус круга, а t - угол.
2. Фракталы
Фракталы - это геометрические фигуры, обладающие самоподобием. Они могут быть как абстрактными, так и иметь конкретное значение. Фракталы можно создавать с помощью итерационных алгоритмов, например, с помощью алгоритма Мандельброта. Этот алгоритм позволяет создавать фракталы на основе простых математических операций, таких как сложение, умножение и возведение в квадрат.
3. Использование таблиц
Для создания сложных и красивых геометрических фигур можно использовать таблицы. В таблице можно задать координаты точек и соединить их линиями или кривыми. Также в таблице можно задать цвета и текстуры для изображений. Используя таблицы, можно создавать разнообразные геометрические узоры, а также объединять несколько фигур в одно изображение.
Трюки и методы математического рисования не имеют ограничений. Это творческий и интересный процесс, в котором можно проявить свою фантазию и математические знания. Надеемся, что эти советы помогут вам в создании уникальных и красивых математических рисунков!
Графическое представление функций
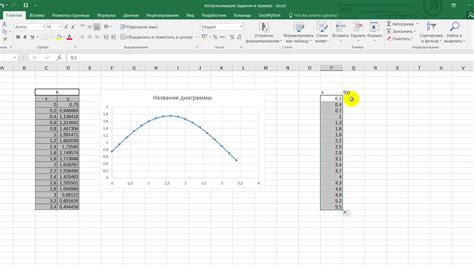
Графическое представление функций позволяет наглядно отобразить их поведение и особенности. При помощи математического рисования можно создавать графики функций, строить диаграммы и распределения данных.
Одним из способов графического представления функций является построение графиков. Для этого необходимо определить область определения функции и построить координатную плоскость. Затем, выбрав несколько точек на плоскости, можно построить график, соединив эти точки линией или кривой. Можно также использовать математические функции для определения формы графика.
Другим способом графического представления функций является построение диаграмм и графиков распределения данных. Например, гистограммы позволяют наглядно представить распределение частоты появления определенных значений. Линейные диаграммы позволяют показать изменение значений во времени.
Графическое представление функций имеет много преимуществ. Во-первых, оно позволяет наглядно представить и проанализировать особенности функции, такие как экстремумы, точки перегиба и асимптоты. Во-вторых, графики и диаграммы позволяют визуально сравнивать функции и данные. В-третьих, они позволяют более эффективно коммуницировать математические концепции с другими людьми.
Искусство математического рисования позволяет создавать красивые и информативные графики и диаграммы. Знание трюков и методов математического рисования поможет вам использовать графическое представление функций для более глубокого понимания математических концепций и их применения в реальном мире.
Теория фракталов

Фракталы можно найти во множестве объектов в природе, начиная от самых простых, таких как ветка дерева или снежинка, до самых сложных, таких как побережье океана.
Одной из основных черт фракталов является их фрактальная размерность, которая может быть нецелым числом. Фрактальная размерность отражает самоподобие фрактала - более детализированные уровни имеют большую размерность, что позволяет описать их структуру.
Для изучения фракталов используются различные математические методы, включая итеративные функции, рекурсию, а также компьютерное моделирование.
Изучение фракталов позволяет не только глубже понять природу окружающих нас объектов, но и применять эту теорию в различных областях, таких как компьютерная графика, физика, биология и даже финансовые рынки.
Одним из известных примеров фрактального объекта является так называемый "треугольник Серпинского", который может быть получен путем рекурсивного деления треугольника на три более маленьких треугольника.
Теория фракталов предлагает нам новый способ взглянуть на мир и открыть его скрытую красоту и гармонию, позволяя нам увидеть математические законы, лежащие в основе всего сущего.
Работа с цветами и оттенками

Цвета и оттенки играют важную роль в создании привлекательных графических изображений. В математическом рисовании также можно использовать различные техники для создания и сочетания цветовых схем.
Одним из основных способов работы с цветами является использование RGB-модели. В этой модели каждый цвет представлен комбинацией красного, зеленого и синего цветов. Путем изменения интенсивности каждого цвета можно получить широкий спектр оттенков.
Для работы с цветами и оттенками можно использовать цветовые схемы, такие как градиенты. Градиент представляет собой плавный переход от одного цвета к другому. Это позволяет создавать превосходные эффекты в рисунках и дизайне.
Еще одним способом работы с цветами является изменение яркости и насыщенности. Путем регулировки яркости можно создать эффекты освещения, а насыщенность позволяет изменить интенсивность цветов.
Важно помнить о контрасте, который влияет на восприятие изображения. Контраст можно создать, комбинируя цвета с противоположными характеристиками или с использованием цветов из разных концов цветовой модели.
Работа с цветами и оттенками требует творческого подхода и экспериментов. Используя математическое рисование, можно достичь потрясающих результатов и создать уникальные и привлекательные изображения.
Применение векторных графиков
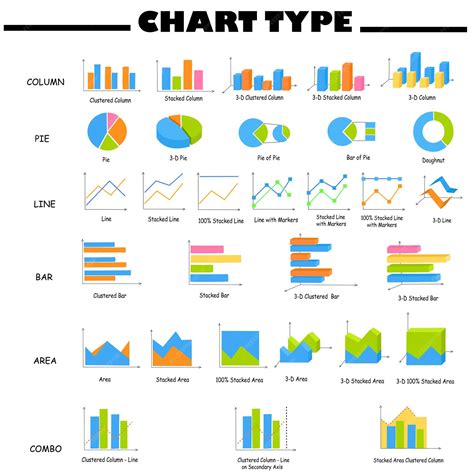
Преимущества использования векторных графиков включают:
- Идеальное качество при любом масштабе: векторные графики можно изменять без потери деталей и размытия изображения. Это особенно полезно при создании логотипов или других дизайнерских элементов, которые необходимо использовать в разных размерах.
- Универсальность: векторные графики могут быть экспортированы в различные форматы, такие как SVG, PDF или EPS, что позволяет использовать их в разных приложениях и на разных устройствах.
- Малый размер файлов: векторные графики обычно занимают меньше места на диске, чем растровые графики. Это особенно важно при работе с большими изображениями или при использовании графики в веб-дизайне для ускорения загрузки страницы.
Применение векторной графики широко распространено в различных областях, таких как:
- Дизайн и искусство: векторные графики позволяют создавать сложные и выразительные иллюстрации, а также дизайнерские элементы для печати или веб-дизайна.
- Геометрическое моделирование: векторные графики используются для представления и обработки трехмерных объектов и архитектурных проектов.
- Информационные графики: векторные графики используются для создания диаграмм, графиков и других визуализаций данных.
Использование векторной графики требует навыков работы с векторными редакторами, такими как Adobe Illustrator или CorelDRAW. При создании векторных изображений необходимо иметь понимание математических операций и знание основных инструментов и функций редактора.
В целом, векторные графики предоставляют много возможностей для создания высококачественных и универсальных изображений и имеют широкое применение в различных областях дизайна, искусства и информационной визуализации.
Использование математических формул в дизайне
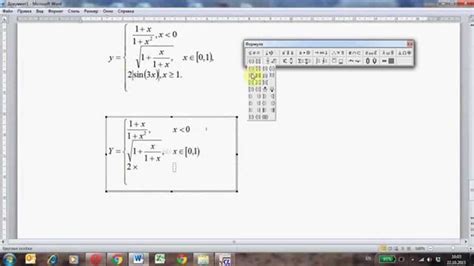
Математические формулы могут быть полезным и красивым элементом для дизайна различных объектов. Возможность использования математических формул открывает дизайнерам огромный потенциал для творчества и создания эстетически привлекательных и функциональных предметов.
Одним из способов использования математических формул в дизайне является создание графических паттернов и узоров. Математические функции могут использоваться для генерации сложных и красивых узоров, которые могут быть размещены на различных поверхностях, таких как одежда, печатные издания или цифровые медиа.
Кроме того, математические формулы могут быть использованы для создания изобразительных арт-объектов. Известным примером является фрактальное искусство, в котором множество различных форм и фигур создается с использованием математической модели фракталов.
Применение математических формул также имеет практическое значение в различных областях. Например, в архитектуре они могут использоваться для проектирования оптимальных и энергоэффективных структур. В инженерии математические формулы могут применяться для определения жесткости и надежности конструкций. В искусственном интеллекте и компьютерной графике математические алгоритмы используются для создания реалистичных и эффектных визуализаций.
| Преимущества использования математических формул в дизайне: |
|---|
| 1. Возможность создания уникальных и сложных узоров и паттернов; |
| 2. Повышение функциональности и эстетической привлекательности объектов дизайна; |
| 3. Получение оптимальных и энергоэффективных структур; |
| 4. Создание реалистичных визуализаций и эффектных арт-объектов; |
| 5. Применение математических моделей для определения параметров и свойств дизайна. |
Использование математических формул в дизайне демонстрирует прекрасный баланс между искусством и наукой. Оно позволяет дизайнерам экспериментировать и создавать уникальные и оригинальные объекты, которые восхищают своей красотой и функциональностью.