У каждого из нас в жизни бывают ситуации, когда необходимо встретиться с кем-то, кто движется в противоположном направлении. На первый взгляд может показаться, что найти точку встречи в таких условиях достаточно сложно, однако на самом деле существуют простые методы, позволяющие решить данную задачу.
Один из самых простых способов найти точку встречи при движении навстречу – использование пропорции. Для этого необходимо знать скорости движения каждого из участников и время, в течение которого они двигаются. При этом основная формула для нахождения точки встречи будет выглядеть следующим образом:
Точка встречи = (Скорость первого участника × Время движения первого участника) / (Скорость первого участника + Скорость второго участника)
Если известна только скорость встречного движения участников, можно воспользоваться формулой:
Точка встречи = (Скорость встречного движения × Время встречи) / 2
Но даже в случае, когда нет точных данных о скорости или времени движения, можно использовать графический метод для нахождения точки встречи. Для этого необходимо нарисовать две прямые, соответствующие движению каждого участника, и найти их точку пересечения.
Теперь рассмотрим пример для наглядного понимания данной задачи. Допустим, что два автомобиля движутся друг навстречу другу. У первого автомобиля скорость составляет 60 км/ч, а у второго – 80 км/ч. Если они двигаются в течение 2 часов, то по формуле получаем:
Точка встречи = (60 × 2) / (60 + 80) = 120 / 140 = 0,85714 часа
Таким образом, точка встречи будет находиться примерно через 51,43 минуты (или 0,85714 часа) от старта первого автомобиля. Используя эти простые методы, вы сможете точно определить время и место вашей встречи при движении навстречу.
Методы поиска точки встречи при движении навстречу
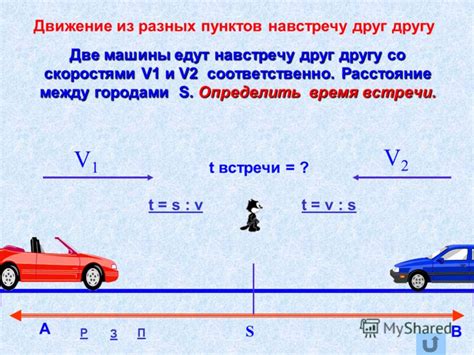
При движении двух объектов по направлению друг на друга, необходимо найти точку и время их встречи. Это может быть полезно в различных сферах, от автомобильной индустрии до физики движения тел.
Существуют несколько методов для определения точки встречи:
1. Метод геометрической интерполяции: при движении объектов по прямым линиям можно воспользоваться методом геометрической интерполяции. Формула для нахождения точки встречи выглядит следующим образом:
x = (x1 * v2 + x2 * v1) / (v1 + v2)
y = (y1 * v2 + y2 * v1) / (v1 + v2)
где (x1, y1) и (x2, y2) - начальные координаты объектов, v1 и v2 - их скорости.
2. Метод перебора: если у объектов нет фиксированных скоростей, можно воспользоваться методом перебора. Зафиксируем разницу времени t между движением объектов и будем изменять координаты объектов для каждого значения t. Если расстояние между объектами станет равным нулю, значит, они встретились.
3. Метод итераций: этот метод похож на метод перебора, но вместо постепенного изменения координат объектов, мы будем изменять время t до тех пор, пока расстояние между объектами не станет равным нулю.
Пример:
Допустим, у нас есть два автомобиля, движущихся навстречу. Первый автомобиль стартует из точки А с координатами (0, 0) и едет со скоростью 50 км/ч, второй автомобиль стартует из точки B с координатами (100, 0) и едет со скоростью 60 км/ч. Мы хотим найти точку и время их встречи.
Используем метод геометрической интерполяции:
x = (0 * 60 + 100 * 50) / (50 + 60) = 2000 / 110 = 18.18
Таким образом, точка встречи находится на расстоянии 18.18 км от начальной точки первого автомобиля.
Использование формулы скорости и времени

Для определения точки встречи при движении навстречу можно использовать формулу скорости и времени. Эта формула позволяет вычислить расстояние между двумя точками и определить время, через которое они встретятся.
Формула скорости и времени выглядит следующим образом:
Расстояние = (Скорость1 * Время) + (Скорость2 * Время)
Где:
- Расстояние - расстояние между двумя точками, которые движутся навстречу друг другу. Это значение можно выразить в километрах, метрах или любых других единицах измерения расстояния.
- Скорость1 - скорость первой точки. Также можно указать единицы измерения скорости, например, километры в час.
- Скорость2 - скорость второй точки. Это значение также может быть выражено в километрах в час или других единицах измерения скорости.
- Время - время, через которое точки встретятся. Обычно это значение выражается в часах или минутах.
Чтобы найти точку встречи, необходимо установить, при каком времени расстояние между точками будет равным нулю. То есть, необходимо решить уравнение, приравняв расстояние к нулю:
(Скорость1 * Время) + (Скорость2 * Время) = 0
Затем, найденное значение времени подставить обратно в формулу скорости и времени, чтобы определить расстояние между точками в этот момент:
Расстояние = (Скорость1 * Время) + (Скорость2 * Время)
Таким образом, используя формулу скорости и времени, можно найти точку встречи при движении навстречу двух точек.
Алгебраический метод решения задачи

Для применения алгебраического метода необходимо рассмотреть движение двух объектов, которые движутся навстречу друг другу. Обозначим их скорости как V1 и V2, а начальные координаты как X1 и X2. Также известно, что объекты встречаются через T единиц времени.
Для определения точки встречи необходимо приравнять координаты объектов в момент встречи X1 + V1 * T = X2 + V2 * T и решить полученное уравнение относительно T.
Пример:
- Объект 1 начинает движение со скоростью V1 = 10 м/с и начальной координатой X1 = 0 м;
- Объект 2 начинает движение со скоростью V2 = 5 м/с и начальной координатой X2 = 100 м;
Необходимо найти время T и координату точки встречи X:
X1 + V1 * T = X2 + V2 * T
0 + 10T = 100 + 5T
5T = 100
T = 20
Таким образом, объекты встретятся через 20 секунд, а координата точки встречи будет равна:
X = X1 + V1 * T = 0 + 10 * 20 = 200 м
Используя алгебраический метод решения задачи, можно точно определить, когда и где произойдет встреча двух движущихся навстречу объектов.
Через концентрические окружности
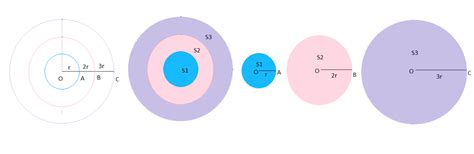
Для нахождения точки встречи при движении навстречу используется метод через концентрические окружности. Этот метод основан на идее, что при движении двух объектов навстречу, встречная точка будет находиться на линии, соединяющей центры окружностей.
Для применения данного метода необходимо знать скорости и начальные координаты движущихся объектов. Первый шаг - определить центры концентрических окружностей. Для этого необходимо найти расстояние между начальными координатами движущихся объектов.
Затем, необходимо определить радиусы окружностей. Радиус первой окружности должен быть равен половине расстояния между объектами, а радиус второй окружности равен сумме радиусов первой окружности и второго объекта.
После определения окружностей необходимо проверить, пересекаются ли они. Если окружности пересекаются, то точка пересечения будет являться точкой встречи объектов.
Если окружности не пересекаются, то встречной точки не существует. В таком случае, можно рассмотреть другие методы для нахождения точки встречи, например, метод через координаты и скорости объектов.
Примеры решения задачи о точке встречи

Ниже приведены два примера простого решения задачи о точке встречи при движении навстречу.
Пример 1:
Пусть первый объект движется со скоростью a м/с, а второй объект движется со скоростью b м/с. Допустим, что они начинают движение в момент времени t=0. Чтобы найти точку встречи, нужно найти время t, при котором два объекта находятся в одном месте.
Рассмотрим следующую таблицу:
| Время, сек | Расстояние первого объекта, м | Расстояние второго объекта, м |
|---|---|---|
| 0 | 0 | 0 |
| 1 | a | b |
| 2 | 2a | 2b |
| ... | ... | ... |
| t | at | bt |
Точка встречи находится в месте, где расстояние первого объекта равно расстоянию второго объекта. Из таблицы видно, что это происходит при значении времени t=a/b. Таким образом, точка встречи находится на расстоянии at=a(a/b)= a2/b от начальной точки.
Пример 2:
Пусть первый объект движется со скоростью a м/с, а второй объект движется со скоростью b м/с. В этом примере мы будем использовать формулу времени:
t = d/(a+b),
где d - расстояние между начальными точками движения объектов.
Таким образом, чтобы найти точку встречи, нужно знать начальные координаты объектов и их скорости.