Шестиугольник - это многоугольник, состоящий из шести сторон и шести углов. Это фигура, которая имеет множество применений в различных областях, включая геометрию, архитектуру и биологию. Найти углы шестиугольника может быть сложной задачей, но существуют различные методы, которые помогут вам выполнить эту задачу с легкостью.
Первый метод основывается на знании, что сумма углов в любом многоугольнике равна (n-2) * 180 градусов, где n - количество углов. Для шестиугольника сумма всех углов будет равна (6-2) * 180 = 720 градусов. Вы можете поделить эту сумму на 6, чтобы найти меру каждого угла. Таким образом, каждый угол равен 720 / 6 = 120 градусам.
Второй метод включает использование свойства равных углов. В шестиугольнике все углы равны друг другу, так как все стороны равны. Это означает, что каждый угол шестиугольника будет равен 180 / 6 = 30 градусам.
Важно помнить, что эти методы работают только для регулярного шестиугольника, то есть такого, у которого все стороны и все углы равны. В случае нерегулярного шестиугольника эти формулы не применимы, и для нахождения углов потребуется использовать другие методы, такие как теоремы о многогранниках или геометрические вычисления.
Методы вычисления углов шестиугольника
1. Разделение на треугольники. Шестиугольник можно разделить на четыре треугольника путем проведения двух диагоналей из одной вершины к противоположным сторонам. Зная углы треугольников, можно вычислить углы шестиугольника с помощью теоремы о сумме углов треугольника.
2. Формула суммы углов. Углы любого многоугольника, включая шестиугольник, обладают свойством суммы. Сумма всех углов шестиугольника равна 720 градусам. Зная значения пяти углов, можно вычислить оставшийся шестой угол.
3. Равномерные углы. Если шестиугольник является правильным, то все его углы равны между собой. В этом случае достаточно знать значение одного угла, а все остальные будут равны.
Важно помнить, что значения углов шестиугольника могут быть найдены только при наличии достаточного количества информации о фигуре, включая длины сторон и другие параметры.
Метод известных углов
Для применения этого метода необходимо знать хотя бы один угол шестиугольника. Зная один угол, мы можем вычислить все остальные углы.
Шаги выполнения метода:
- Найдите известный угол шестиугольника. Назовем его A.
- Вычислите сумму всех углов шестиугольника, если известен угол A.
- Вычтите из суммы всех углов шестиугольника угол A, чтобы найти сумму остальных пяти углов.
- Разделите сумму остальных углов на 5, чтобы найти меру каждого угла.
Таким образом, метод известных углов позволяет найти все углы шестиугольника, если известен хотя бы один угол. Это полезный инструмент для решения задач геометрии, связанных со шестиугольниками.
Метод соответствующих углов
Для применения метода необходимо произвести следующие шаги:
- Выбрать любую сторону шестиугольника и провести ее продолжение, создавая внешний угол.
- Измерить внешний угол шестиугольника при помощи транспортира или другого инструмента.
- Выразить внешний угол в градусах.
- Найти противоположный внутренний угол, который образован той же стороной и продолжением соседней стороны шестиугольника.
- Выразить противоположный внутренний угол в градусах.
- Вычислить сумму найденных внешнего и противоположного внутреннего углов.
- Вычислить разницу между полученной суммой и 360 градусов.
Таким образом, метод соответствующих углов позволяет найти недостающие углы шестиугольника, используя свойство суммы внешних углов. Этот метод удобен в тех случаях, когда известны значения некоторых углов шестиугольника и требуется найти остальные.
Метод взаимно противоположных углов
Для применения метода взаимно противоположных углов необходимо знать значения двух смежных углов шестиугольника. Пусть это будут углы A и B.
Шаги алгоритма:
- Вычислить внутренний угол C по формуле: C = 360° - A - B
- Найти противоположный угол D, вычитая угол C из 360°: D = 360° - C
- Рассчитать оставшиеся углы E и F, разделив угол D на две равные части: E = D / 2 и F = D / 2
Таким образом, применяя метод взаимно противоположных углов, можно найти все углы шестиугольника, имея всего лишь два известных значения.
Пример:
| Угол A | Угол B | Угол C | Угол D | Угол E | Угол F |
|---|---|---|---|---|---|
| 60° | 120° | 180° | 180° | 90° | 90° |
В данном примере мы знаем значения углов A и B (60° и 120°). После выполнения всех шагов алгоритма получаем значения всех углов шестиугольника: C = 180°, D = 180°, E = 90°, F = 90°.
Метод суммы углов
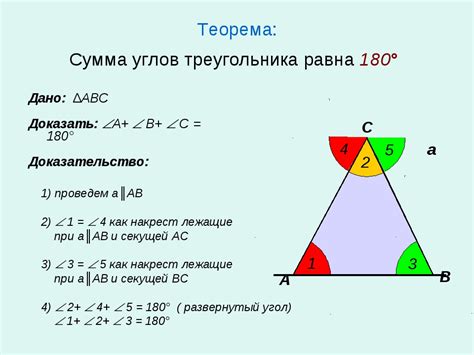
Для применения данного метода необходимо использовать следующую формулу:
| Сумма углов | Формула |
|---|---|
| Сумма всех углов шестиугольника | 360° |
| Сумма внешних углов шестиугольника | 360° |
| Сумма внутренних углов шестиугольника | (6 - 2) × 180° |
Используя формулу суммы внутренних углов шестиугольника, мы можем найти значения каждого из углов, зная только некоторые из них. Например, если известны значения двух углов, остальные четыре можно найти, вычислив сумму внутренних углов и вычитая из нее известные значения.
Метод суммы углов является основным при решении задач на нахождение углов шестиугольника, основываясь на известных значениях.
Метод площадей треугольников, образованных шестиугольником
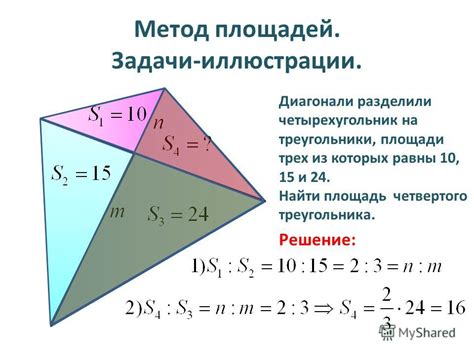
Один из методов нахождения углов шестиугольника основан на использовании площадей треугольников, образованных внутри шестиугольника.
Для применения этого метода необходимо следующее:
- Разделить шестиугольник на четыре треугольника, проведя две диагонали, которые не пересекаются.
- Найдите площади всех треугольников, используя формулу площади треугольника: S = 0.5 * a * b * sin(C), где S - площадь треугольника, a и b - длины сторон треугольника, C - угол между этими сторонами.
- Сложите площади двух противоположных треугольников. Полученные суммы равны и могут быть обозначены как S1 и S2.
- Вычислите площади оставшихся двух треугольников. Обозначим их как S3 и S4.
- Найдите величину угла между противоположными сторонами шестиугольника, используя формулу S1/S2 = sin(A)/sin(B), где A и B - углы между противоположными сторонами шестиугольника.
- Повторите шаги 3-5 для оставшихся углов, получив значения для радиусов шестиугольника.
Таким образом, метод площадей треугольников позволяет вычислить значения углов шестиугольника, используя только информацию о площадях треугольников, образованных внутри него.