Одним из основных способов нахождения решений уравнения касательной является использование метода касательных отношений. Этот метод основан на том, что касательная является предельным положением секущей, проходящей через две точки кривой.
При использовании метода касательных отношений необходимо найти уравнение секущей, проходящей через две заданные точки кривой. Затем следует устремить расстояние между точками к нулю, чтобы получить уравнение касательной. Это позволяет найти координаты точки, в которой секущая пересекает кривую и, следовательно, найти уравнение касательной.
Другим способом решения уравнения касательной является использование метода дифференцирования. Этот метод основан на связи между уравнением касательной и производной функции, задающей кривую. Производная функции определяет тангенс угла наклона касательной в каждой точке кривой.
При использовании метода дифференцирования необходимо найти производную функции, задающей кривую. Затем следует подставить в уравнение касательной координаты точки, в которой нужно найти касательную, и производную функции в данной точке. Это позволит найти уравнение касательной и коэффициент наклона касательной в заданной точке кривой.
Методы нахождения касательной
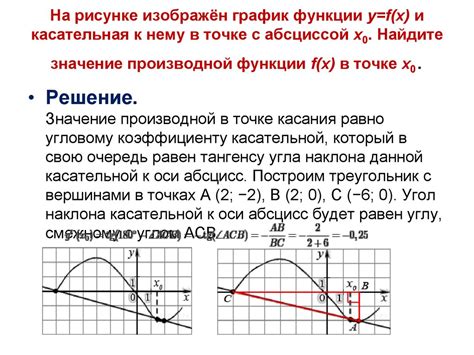
Один из наиболее распространенных методов нахождения касательной - использование геометрической интерпретации производной. Для этого необходимо найти производную функции в данной точке, а затем использовать ее значение для определения наклона касательной. Кроме того, можно найти точку пересечения касательной с осью ординат и использовать ее для построения уравнения касательной.
Другим методом нахождения касательной является использование формулы дифференцирования. Для этого нужно сначала выразить функцию через переменную, а затем применить соответствующую формулу для нахождения производной. Затем можно использовать найденное значение производной для определения наклона касательной и построения ее уравнения.
Также существуют численные методы нахождения касательной, которые основаны на представлении функции в виде таблицы значений или графика. Один из таких методов - метод конечной разности. Он основан на приближенном вычислении производной функции путем разделения функции на маленькие интервалы и вычисления наклона соседних точек. Этот метод особенно полезен, если у функции нет аналитического выражения и доступны только ее значения.
| Метод | Описание |
|---|---|
| Геометрическая интерпретация | Нахождение наклона касательной с использованием производной функции и точки пересечения с осью ординат |
| Формула дифференцирования | Выражение функции через переменную и применение соответствующей формулы для нахождения производной |
| Численные методы | Использование таблицы значений или графика для аппроксимации производной и нахождения наклона касательной |
В зависимости от конкретной задачи и доступной информации можно выбрать подходящий метод нахождения касательной. Это поможет получить более точные результаты и лучше понять свойства функции в заданной точке.
Геометрический метод

Для применения геометрического метода необходимо знать уравнение касательной и координаты точки, в которой касательная проведена. С помощью геометрических построений можно найти точки касания и проанализировать связь между ними.
Основной принцип геометрического метода заключается в том, что касательная к графику функции в точке перпендикулярна радиусу, проведенному из данной точки к касательной.
Для применения геометрического метода необходимо:
Шаг 1: Записать уравнение функции, для которой требуется найти уравнение касательной.
Шаг 2: Записать уравнение касательной в общем виде.
Шаг 3: Найти координаты точки, в которой проведена касательная.
Шаг 4: Найти производную функции и вычислить ее значение в точке касания.
Шаг 5: Составить уравнение прямой, проходящей через заданную точку и имеющей тот же угловой коэффициент, что и касательная.
Шаг 6: Упростить полученное уравнение и записать его в общем виде.
Геометрический метод решения уравнения касательной позволяет графически представить результаты и проанализировать их. Он может быть полезен при решении задач, связанных с геометрией и аналитической геометрией.
Аналитический метод

Аналитический метод решения уравнения касательной позволяет найти точные значения корней без необходимости использования приближенных численных методов. Этот метод основан на аналитической геометрии и дифференциальном исчислении.
Для применения аналитического метода необходимо выразить уравнение касательной в явном виде и решить его аналитически. Это требует знания математических формул и свойств функций, а также навыков работы с дифференциальными уравнениями.
Аналитический метод решения уравнения касательной позволяет получить точные значения корней и более подробное представление графика функции в окрестности этих корней. Однако он требует более сложных вычислений и может быть применен не для всех функций.
Применение аналитического метода решения уравнения касательной позволяет получить более точные результаты и углубить понимание свойств функций. Это особенно полезно при исследовании сложных функций или при решении задач, требующих точных значений корней.
Численные методы

Один из наиболее распространенных численных методов - метод Ньютона. Он основан на локальной аппроксимации функции с помощью касательной. Используя эту аппроксимацию, метод Ньютона выполняет итерационный процесс для нахождения корня уравнения.
| Шаг | Формула |
|---|---|
| 1 | xn+1 = xn - f(xn) / f'(xn) |
| 2 | Повторить шаг 1 до достижения необходимой точности |
Другим численным методом является метод деления пополам, или бинарный поиск. Он базируется на принципе разделения отрезка, содержащего корень, на две равные части. Затем процесс деления повторяется до достижения необходимой точности.
Метод секущих - еще один численный метод, который также использует аппроксимацию касательной, но в отличие от метода Ньютона, аппроксимация основана на двух точках, а не одной. Метод секущих также производит последовательные итерации до достижения необходимой точности.
Решение уравнения касательной с использованием численных методов является эффективным и точным способом нахождения корня уравнения. Выбор конкретного метода зависит от требуемой точности, времени выполнения и других особенностей задачи.
Решение уравнений касательных

Существуют различные методы решения уравнений касательных, в зависимости от типа задачи и формы уравнения. Рассмотрим некоторые из них:
- Метод дифференцирования: данный метод основан на нахождении производной функции в точке касания. Если уравнение касательной задано в виде y = f(x), то производная f'(x) позволяет определить наклон касательной прямой.
- Метод геометрических построений: этот метод основан на геометрических свойствах кривых и касательных. Он позволяет определить точки касания и построить касательную прямую с помощью компаса и линейки.
- Метод линеаризации: данный метод используется для линеаризации нелинейных уравнений. Он позволяет заменить сложные функции линейными приближениями и получить уравнение касательной в виде прямой линии.
Выбор конкретного метода зависит от поставленной задачи и свойств исходного уравнения. Некоторые задачи могут быть решены более эффективно с использованием дифференцирования, в то время как другие требуют применения геометрических построений или линеаризации.
Важно отметить, что решение уравнений касательных может быть сложной задачей, требующей глубоких знаний математического анализа и геометрии. Поэтому при решении подобных задач рекомендуется обратиться к учебникам и дополнительным материалам, чтобы изучить конкретный метод и примеры его применения.