Извлечение корня третьей степени из числа является одной из важнейших операций в математике. Это представляет собой процесс нахождения числа, которое возведенное в куб, равно заданному числу. Для этого существует несколько эффективных способов и методов, которые могут быть использованы в различных ситуациях.
Один из основных способов извлечения корня третьей степени из числа – это использование встроенных функций в математических пакетах языков программирования. Например, в языке Python можно воспользоваться функцией pow(x, 1/3) для извлечения корня третьей степени из числа. Подобные функции присутствуют и в других популярных языках программирования, таких как Java, C++ и Matlab.
Еще один способ извлечения корня третьей степени из числа – это использование метода Ньютона. Этот метод основан на принципе итераций и позволяет найти приближенное значение корня третьей степени. Для этого необходимо выбрать начальное приближение и последовательно уточнять его использованием формулы x = (2*x + n/(x*x))/3, где n – заданное число, а x – текущее приближение корня. Метод Ньютона обладает высокой точностью и широко применяется в научных и инженерных расчетах.
Извлечение корня третьей степени из числа – это важная математическая операция, которая находит широкое применение в различных областях. Правильный выбор метода и способа может существенно повысить эффективность и точность результата. В данной статье мы рассмотрели основные способы и методы извлечения корня третьей степени из числа и надеемся, что они окажутся полезными в вашей работе.
Методы и способы извлечения корня третьей степени из числа
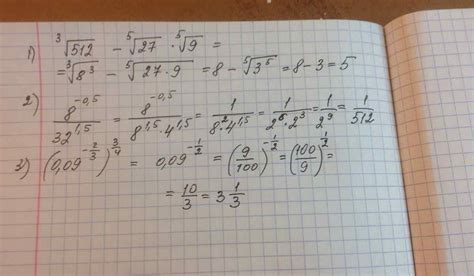
- Метод возведения в степень: данный метод основывается на свойстве степени и позволяет быстро и точно вычислить корень третьей степени. Сначала число возводится в степень 1/3, затем полученное значение округляется до ближайшего целого числа.
- Метод Ньютона: данный метод основывается на итерационной процедуре и позволяет приближенно вычислить корень третьей степени. Начальное приближение выбирается произвольным образом, затем используется формула для вычисления следующего приближения. Процедура повторяется, пока разность между текущим и предыдущим приближениями не станет меньше заданной точности.
- Метод инверсии: данный метод основывается на представлении корня третьей степени как обратного значения степени. То есть, вместо извлечения корня третьей степени из числа, мы извлекаем обратное значение этого числа в кубическую степень.
Каждый из этих методов имеет свои преимущества и недостатки, и выбор метода зависит от требуемой точности и вычислительных ресурсов, которыми вы располагаете. Использование этих методов позволяет эффективно извлекать корень третьей степени из числа и применять его в различных математических задачах.
Эффективные приемы для извлечения корня
Один из самых простых способов извлечения корня третьей степени - это использование кубического корня. Кубический корень числа можно найти с помощью специальных калькуляторов или с помощью математических функций в программном обеспечении, таком как Python или Excel.
Если вам необходимо выполнить вычисление вручную, можно воспользоваться таблицей кубических корней. В таблице перечислены значения кубических корней для различных чисел. Найдите ближайшее значение из таблицы и примените следующую формулу:
∛x ≈ y * (x/y^2)
где x - число, из которого необходимо извлечь корень, а y - ближайшее значение из таблицы кубических корней.
| Число | Кубический корень |
|---|---|
| 1 | 1 |
| 2 | 1.26 |
| 3 | 1.44 |
| 4 | 1.58 |
| 5 | 1.71 |
Если точность очень важна, можно использовать итерационные алгоритмы, такие как метод Ньютона-Рафсона. Эти алгоритмы позволяют найти значения корня с высокой точностью и приемлемой скоростью вычислений.
Итак, есть несколько эффективных приемов для извлечения корня третьей степени из числа. Вы можете воспользоваться кубическим корнем, таблицей кубических корней или итерационными алгоритмами в зависимости от ваших потребностей.