Одной из фундаментальных теорем геометрии является теорема косинусов, которая позволяет нам вычислять длины сторон треугольника, зная длины двух сторон и косинуса между ними. Это очень полезное свойство, которое находит применение в различных областях знаний, начиная от физики и заканчивая архитектурой и строительством.
Если у вас есть треугольник, угол при вершине которого вы хотите вычислить, но известна только длина двух сторон и косинус этого угла, то вы можете легко найти длину третьей стороны. Для этого применяется формула, известная как теорема косинусов. Она гласит: квадрат длины третьей стороны равен сумме квадратов длин двух известных сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Таким образом, зная две длины сторон треугольника и косинус угла между ними, мы можем без труда рассчитать длину третьей стороны. Этот способ очень удобен, так как позволяет сократить время и усилия, которые необходимы для нахождения неизвестной стороны, особенно когда требуется множество вычислений.
Формула для нахождения стороны треугольника по косинусу угла:
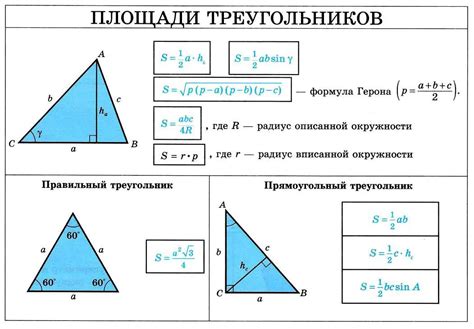
Для нахождения стороны треугольника по известному косинусу угла можно использовать формулу:
| Формула | Описание |
|---|---|
| a = c * cos(α) | где a - искомая сторона треугольника, c - гипотенуза, α - угол между гипотенузой и стороной a |
В данной формуле известны гипотенуза и косинус угла α. Умножив гипотенузу на значение косинуса угла, мы получим длину искомой стороны треугольника.
Данная формула может быть полезна при решении различных геометрических задач, например, при нахождении сторон прямоугольного треугольника по известным углам.
Знакомство с основным понятием

В треугольнике ABC, где угол С является прямым углом, косинус угла А (cos A) определяется следующим образом:
- cos A = BC / AC
То есть, косинус угла равен отношению длины катета к длине гипотенузы.
Используя это определение, мы можем вычислить длину стороны треугольника, зная значение косинуса угла и длину другой стороны. Например, если известны косинус угла и длина гипотенузы, мы можем найти длину катета.
Задачи, в которых применяется формула

1. Вычисление неизвестной стороны треугольника.
Если известны длина одной стороны треугольника и косинус угла, напротив этой стороны, можно легко найти длину неизвестной стороны. Данная формула позволяет решить подобные задачи без необходимости проведения дополнительных измерений или использования других формул.
2. Определение соотношений между сторонами и углами треугольника.
Формула дает возможность установить зависимости между сторонами и углами треугольника. Например, в случае, когда два треугольника имеют одинаковые углы и разные стороны, можно сравнивать их размеры, применяя данную формулу.
3. Решение задач на поиск площади треугольника.
Одним из важных шагов при вычислении площади треугольника является нахождение длин сторон. Поэтому формула для нахождения стороны треугольника по косинусу угла может быть использована в данном контексте. Зная длину стороны и косинус противоположного угла, можно легко вычислить площадь треугольника.
Необходимо отметить, что формула для нахождения стороны треугольника по косинусу угла является лишь одним из инструментов, применяемых в геометрии и тригонометрии. Ее использование зависит от конкретной задачи и условий, в которых она поставлена.
Определение значения косинуса угла

Зная значения катетов и гипотенузы, мы можем вычислить значение косинуса угла с помощью простой формулы:
cos(угол) = прилежащий катет / гипотенуза
Значение косинуса угла всегда будет находиться в интервале от -1 до 1, где -1 соответствует прямому углу (180 градусов или π радиан) и 1 соответствует нулевому углу (0 градусов или 0 радиан).
Косинус угла широко используется в различных областях, включая геометрию, физику, статистику и компьютерную графику. Он позволяет нам определить расстояние между точками на плоскости, оценить силу и энергию системы, вычислять вероятности событий и даже создавать реалистичные 3D-изображения.
Простой способ расчета

Для нахождения стороны треугольника по косинусу угла существует простая формула, которая поможет вам быстро и точно выполнить расчеты.
Допустим, у нас есть треугольник со сторонами a, b и c, и углом α, противолежащим стороне a. Косинус угла α обозначается как cos(α).
Формула для нахождения стороны треугольника по косинусу угла:
a = c * cos(α).
Для того чтобы найти значение стороны a, необходимо знать длину стороны c и значение косинуса угла α.
Пример расчета:
Пусть c = 5 и cos(α) = 0.8.
Тогда, подставляя значения в формулу:
a = 5 * 0.8 = 4.
Таким образом, сторона треугольника a равна 4.
Используя этот простой способ расчета, вы можете легко найти сторону треугольника по косинусу угла.
Быстрый метод применения формулы

Для нахождения стороны треугольника по косинусу угла можно использовать следующую формулу:
$$a = \frac{c}{\cos \alpha}$$
Где:
- $a$ - искомая сторона треугольника
- $c$ - известная сторона треугольника
- $\alpha$ - угол между известной и искомой сторонами
Для применения данной формулы необходимо знать длину одной из сторон треугольника и значение косинуса угла между этой стороной и искомой стороной.
Пример:
Пусть известная сторона треугольника равна $5$, а косинус угла $\alpha$ равен $0.8$. Тогда мы можем найти искомую сторону по формуле:
$$a = \frac{5}{0.8} = 6.25$$
Таким образом, искомая сторона треугольника равна $6.25$.
Примеры задач для самостоятельного решения
Для закрепления полученных знаний по нахождению стороны треугольника по косинусу угла предлагаем решить следующие задачи:
| Задача | Условие |
|---|---|
| Задача 1 | В треугольнике ABC известны стороны a = 7 и b = 9 см, а также косинус угла между этими сторонами cos(C) = 0.8. Найдите сторону c треугольника. |
| Задача 2 | В прямоугольном треугольнике ABC против угла B лежит сторона b = 5 см и известен косинус угла A cos(A) = 0.6. Найдите длину гипотенузы c треугольника. |
| Задача 3 | В равностороннем треугольнике ABC известен косинус угла 60°. Найдите сторону a треугольника. |
Постарайтесь самостоятельно решить данные задачи, использовав полученные знания о формуле нахождения стороны треугольника по косинусу угла. Если возникнут трудности, вы можете обратиться к решениям в конце статьи.