Площадь – одна из основных характеристик геометрических фигур, которая позволяет нам определить, сколько плоскостей занимает данная фигура. Зная площадь, мы можем рассчитать ее объем или выбрать подходящую площадь для строительства дома или садового участка. В этой статье мы рассмотрим, как найти площадь треугольника, трапеции и параллелограмма.
Треугольник – это геометрическая фигура, состоящая из трех сторон и трех углов. Чтобы найти площадь треугольника, нужно знать длины его сторон или длину одной стороны и высоту, опущенную на эту сторону. Формула для расчета площади треугольника имеет вид: S = (a * h) / 2, где S – площадь, a – длина основания, h – высота, опущенная на это основание. Если известны длины всех сторон треугольника, можно воспользоваться формулой Герона: S = √(p * (p - a) * (p - b) * (p - c)), где p = (a + b + c) / 2 – полупериметр треугольника, а a, b, c – длины сторон.
Трапеция – это четырехугольник с двумя параллельными сторонами. Чтобы найти площадь трапеции, нужно знать длины двух параллельных сторон и высоту, опущенную на эту параллельную сторону. Формула для расчета площади трапеции имеет вид: S = ((a + b) * h) / 2, где S – площадь трапеции, a, b – длины параллельных сторон, h – высота, опущенная на параллельные стороны. Иногда площадь трапеции можно найти, зная диагонали и угол между ними. Для этого используется формула: S = (d1 * d2 * sin(α)) / 2, где S – площадь, d1, d2 – диагонали трапеции, α – угол между диагоналями.
Параллелограмм – это четырехугольник с противоположными сторонами, параллельными друг другу. Чтобы найти площадь параллелограмма, нужно знать длину одной из его сторон и высоту, опущенную на эту сторону. Формула для расчета площади параллелограмма имеет вид: S = a * h, где S – площадь, a – длина стороны, h – высота, опущенная на эту сторону. Также площадь параллелограмма можно найти, зная длины двух сторон и угол между ними. Для этого используется формула: S = a * b * sin(α), где S – площадь, a, b – длины сторон, α – угол между сторонами.
Треугольник
У треугольника есть несколько способов найти его площадь, в зависимости от информации, которая изначально известна:
| Известные величины | Формула площади |
|---|---|
| Длины двух сторон и угол между ними | S = (a * b * sin(C)) / 2 |
| Длины всех трех сторон (формула Герона) | S = sqrt(p * (p - a) * (p - b) * (p - c)), где p - полупериметр треугольника |
В первом случае для вычисления площади треугольника необходо знать длины двух сторон и величину угла между ними. Вторая формула позволяет рассчитать площадь треугольника, зная длины всех его сторон.
Площадь треугольника можно также выразить через длину одной стороны и высоту, опущенную на эту сторону из противоположного угла. Формула для этого случая выглядит следующим образом:
S = (a * h) / 2
Где a - длина стороны, h - высота треугольника.
Треугольник имеет большое значение в геометрии из-за своих уникальных свойств и связей с другими фигурами. Изучение треугольников позволяет обобщить многие геометрические понятия и алгоритмы.
Площадь треугольника по формуле Герона

Формула Герона позволяет рассчитать площадь треугольника по длинам его сторон. Для этого необходимо знать длины всех трех сторон треугольника.
Формула для вычисления площади треугольника по формуле Герона выглядит следующим образом:
| S = √(p*(p-a)*(p-b)*(p-c)) |
где S - площадь треугольника, p - полупериметр треугольника (p = (a+b+c)/2), a, b, c - длины сторон треугольника.
Для вычисления площади треугольника по формуле Герона необходимо знать длины всех трех его сторон. После подстановки значений в формулу и выполнения необходимых математических операций получаем значение площади треугольника.
Формула Герона является точным методом расчета площади треугольника и применяется в различных областях геометрии и техники. Она особенно полезна при работе с треугольниками, у которых известны длины сторон, но нет возможности определить высоты.
Трапеция
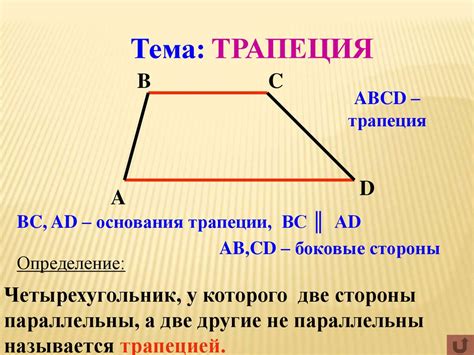
Чтобы найти площадь трапеции, нужно знать ее высоту и длины двух параллельных сторон.
- Высота трапеции - это перпендикуляр, опущенный из одной параллельной стороны на другую.
- Длина оснований - это две параллельные стороны трапеции.
Формула для нахождения площади трапеции:
S = ((a + b) / 2) * h
Где:
- a и b - длины оснований трапеции
- h - высота трапеции
- S - площадь трапеции
Уникальные свойства трапеции:
- Сумма углов трапеции равна 360 градусов.
- Трапеция может быть равнобедренной, когда длины одного избокового ребра равны.
- Диагонали трапеции делятся пополам в точке их пересечения (точке середины).
Площадь трапеции через основания и высоту
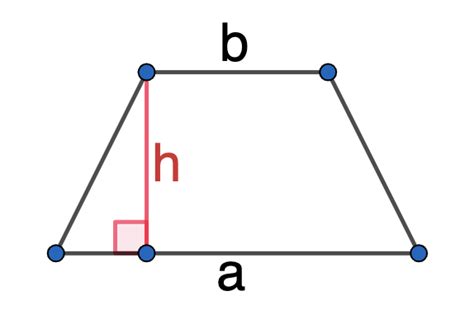
S = (a + b) * h / 2
где
S - площадь трапеции;
a и b - длины оснований;
h - высота трапеции, которая представляет собой перпендикулярное расстояние между основаниями.
Чтобы найти площадь трапеции, необходимо знать длины ее оснований и высоту. После этого просто подставьте значения в формулу и выполните необходимые вычисления.
Также существует другая формула для нахождения площади трапеции, в которой используется длина одного из оснований и длина боковой стороны:
S = (a + b) * h / 2
где
S - площадь трапеции;
a - длина основания;
b - длина боковой стороны, которая соединяет основания;
h - высота трапеции, которая представляет собой перпендикулярное расстояние между основаниями.
Оба этих способа вычисления площади трапеции дадут вам правильный результат, если будут использованы правильные значения для оснований и высоты.
| Примеры вычисления площади трапеции | |
|---|---|
| Длина основания A | 5 см |
| Длина основания B | 7 см |
| Высота | 3 см |
| Площадь | 24 см² |
Важно помнить, что все значения должны быть в одном и том же измерении (например, сантиметры) для правильного вычисления площади.
Параллелограмм
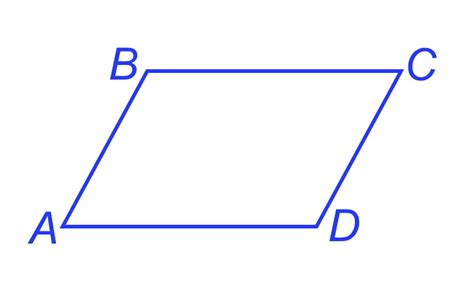
Формула для вычисления площади параллелограмма:
S = a * h,
где S - площадь параллелограмма, a - длина одной из сторон, h - высота, проведенная к этой стороне.
Также площадь параллелограмма можно найти с помощью формулы:
S = a * b * sin(α),
где α - угол между сторонами параллелограмма, a и b - длины соседних сторон.
Для нахождения периметра параллелограмма необходимо сложить длины всех его сторон:
P = 2a + 2b,
где P - периметр параллелограмма, a и b - длины соседних сторон.
Площадь параллелограмма через основание и высоту
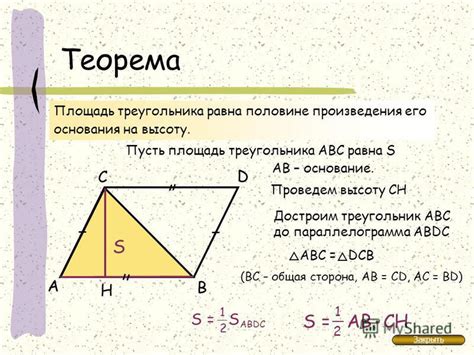
Для расчета площади параллелограмма можно использовать формулу, которая основывается на длине его основания и высоты.
Формула для вычисления площади параллелограмма:
S = основание * высота
где:
S - площадь параллелограмма,
основание - длина одной из его сторон, которая параллельна и противоположна высоте,
высота - расстояние между сторонами, противоположными основанию.
Найдя длину основания и высоту параллелограмма, можно подставить их значения в формулу и получить его площадь.
Пример:
Допустим, длина основания параллелограмма равна 8 см, а его высота равна 5 см. Чтобы найти его площадь, нужно умножить длину основания на высоту:
Площадь = 8 см * 5 см = 40 см².
Таким образом, площадь данного параллелограмма равна 40 квадратным сантиметрам.
Площадь параллелограмма по модулю векторного произведения
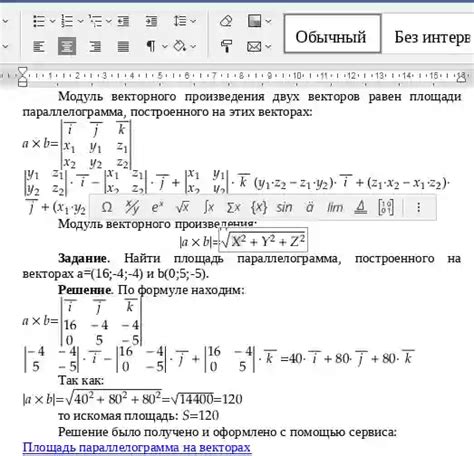
Площадь параллелограмма может быть вычислена с использованием модуля векторного произведения его сторон. Для вычисления площади параллелограмма необходимо выполнить следующие шаги:
| 1. Найдите величину векторного произведения двух векторов, образующих стороны параллелограмма: |
| AB × BC = |AB| × |BC| × sin(θ), |
| где AB и BC - векторы, образующие стороны параллелограмма, |AB| и |BC| - их длины, а θ - угол между ними. |
| 2. Вычислите модуль векторного произведения: |
| |AB × BC| = |AB| × |BC| × sin(θ). |
| 3. Площадь параллелограмма равна модулю векторного произведения: |
| S = |AB × BC|. |
Используя данные этой формулы, можно вычислить площадь параллелограмма, зная длины его сторон и угол между ними. Этот метод находит широкое применение в геометрии и физике.
Сравнение площадей треугольника, трапеции и параллелограмма
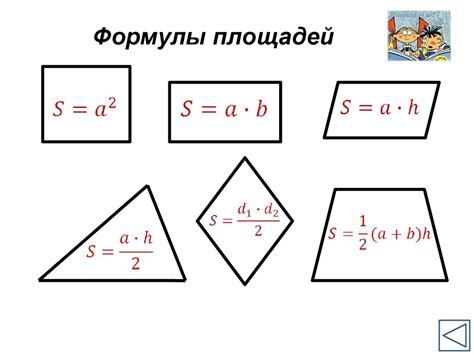
Треугольник: площадь треугольника можно вычислить, зная длины его сторон и высоту, проведенную к одной из сторон. Формула для расчета площади треугольника: S = 0.5 * a * h, где a - длина основания треугольника, h - высота, опущенная к этому основанию. Таким образом, площадь треугольника зависит от длины основания и высоты.
Трапеция: площадь трапеции можно вычислить, зная длины ее оснований и высоту. Формула для расчета площади трапеции: S = 0.5 * (a + b) * h, где a и b - длины оснований трапеции, h - высота трапеции. Таким образом, площадь трапеции зависит от суммы длин оснований и высоты.
Параллелограмм: площадь параллелограмма можно вычислить, зная длину одной из его сторон и высоту, проведенную к этой стороне. Формула для расчета площади параллелограмма: S = a * h, где a - длина основания параллелограмма, h - высота, опущенная к этому основанию. Таким образом, площадь параллелограмма зависит только от длины одной из его сторон и высоты.
Таким образом, при сравнении площадей треугольника, трапеции и параллелограмма необходимо учитывать их форму и размеры, а также использовать соответствующие формулы для вычисления площади каждой из этих геометрических фигур.