Прямоугольные треугольники - одна из самых распространенных и изучаемых геометрических фигур. Они имеют много полезных свойств и широкий спектр применений. Одним из ключевых навыков в работе с прямоугольными треугольниками является нахождение их сторон - гипотенузы и катетов. В этом руководстве мы рассмотрим несколько способов, которые помогут вам найти стороны прямоугольного треугольника.

Первый и наиболее простой способ нахождения сторон прямоугольного треугольника - использование теоремы Пифагора. Согласно этой теореме, квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов. Таким образом, если известны два катета, можно легко найти гипотенузу, просто возведя их в квадрат и сложив результаты.

Если вам известны длины двух сторон прямоугольного треугольника, но неизвестна гипотенуза, вы можете использовать теорему Пифагора, чтобы найти ее. Возможно, вам придется решить квадратное уравнение, чтобы получить значение гипотенузы. Не поленитесь, запишите уравнение и внимательно решите его, используя соответствующую формулу.

Наконец, есть способ найти длину катета прямоугольного треугольника, если известны длины гипотенузы и другого катета. Создавая пропорцию из отношения длин катетов и гипотенузы (катет делится на гипотенузу), вы можете переставить части уравнения, чтобы найти значение длины неизвестного катета.

Поиск сторон прямоугольного треугольника: основное руководство

Чтобы найти стороны прямоугольного треугольника, необходимо знать хотя бы одну сторону и хотя бы один угол треугольника. Существует несколько методов для нахождения сторон прямоугольного треугольника, включая использование теоремы Пифагора, тригонометрические функции и геометрические свойства.

1. Теорема Пифагора:

Теорема Пифагора утверждает, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Если известны длины двух сторон треугольника, можно найти длину третьей стороны с помощью этой теоремы.

2. Тригонометрические функции:

Тригонометрические функции, такие как синус, косинус и тангенс, можно использовать для нахождения неизвестных сторон прямоугольного треугольника. Например, если известен один угол и одна сторона, можно использовать тангенс угла для нахождения длины другой стороны.

3. Геометрические свойства:

Прямоугольный треугольник обладает рядом геометрических свойств, которые можно использовать для нахождения сторон. Например, высота, проведенная к гипотенузе, делит треугольник на две подобные части. Используя эту свойство, можно найти отношение между сторонами треугольника.

Имейте в виду, что для полного определения сторон прямоугольного треугольника необходимо знать как минимум одну сторону и один угол. Чем больше данных известно, тем точнее можно вычислить стороны треугольника. Если известны только две стороны, без информации об угле, возможны множественные решения.

В зависимости от известных данных и специфики задачи, один из методов может оказаться более удобным для нахождения сторон прямоугольного треугольника. Экспериментируйте и выбирайте наиболее подходящий метод для вашей конкретной ситуации.

Определение прямоугольного треугольника

Для определения прямоугольного треугольника существует теорема Пифагора, которая гласит: в квадрате гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

Из этой теоремы можно вывести формулу для нахождения длины гипотенузы, катетов и площади прямоугольного треугольника:

1. Длина гипотенузы (c) можно найти по формуле: c = √(a² + b²), где a и b - длины катетов.
2. Длина каждого катета (a или b) можно найти по формуле: a = √(c² - b²) или b = √(c² - a²), где c - длина гипотенузы, a и b - длины катетов.
3. Площадь прямоугольного треугольника можно найти по формуле: S = (a * b) / 2, где S - площадь, a и b - длины катетов.

Используя эти формулы, можно легко определить стороны прямоугольного треугольника и вычислить его площадь.

Связь между сторонами прямоугольного треугольника и его углами

В прямоугольном треугольнике существует прямая зависимость между длинами его сторон и значениями его углов. Эта связь определяется тремя основными тригонометрическими функциями: синусом, косинусом и тангенсом.

Синус угла в прямоугольном треугольнике равен отношению длины противоположенной стороны к гипотенузе. Иными словами, синус угла определяет, насколько вертикально смещена сторона треугольника относительно его гипотенузы.

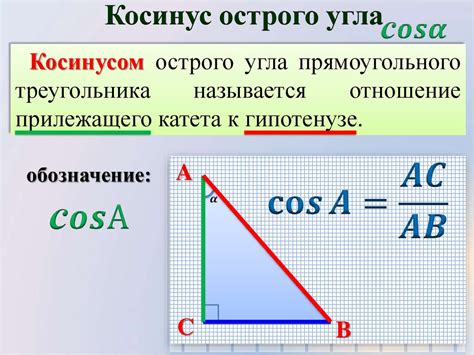
Косинус угла в прямоугольном треугольнике равен отношению длины прилежащей стороны к гипотенузе. Косинус угла показывает, насколько горизонтально смещена сторона треугольника относительно его гипотенузы.

Тангенс угла в прямоугольном треугольнике равен отношению длины противоположенной стороны к длине прилежащей стороны. Тангенс угла определяет, насколько крутая наклон стороны треугольника относительно гипотенузы.

Используя соотношения, полученные с помощью тригонометрических функций, возможно выразить длины сторон прямоугольного треугольника через значения его углов и гипотенузу.

Использование основных тригонометрических функций

Самые важные тригонометрические функции - синус (sin), косинус (cos) и тангенс (tan). Каждая из этих функций имеет свою формулу и позволяет найти значения углов или сторон треугольника.

• Синус угла можно рассчитать, разделив противоположную сторону треугольника на его гипотенузу: sin(A) = a / c.
• Косинус угла можно рассчитать, разделив прилежащую сторону треугольника на его гипотенузу: cos(A) = b / c.
• Тангенс угла можно рассчитать, разделив противоположную сторону треугольника на его прилежащую сторону: tan(A) = a / b.

Зная значения двух сторон и одного угла прямоугольного треугольника, можно применить тригонометрические функции для нахождения значения остальных сторон или углов. Например, если известны гипотенуза c и угол A, можно найти значения сторон a и b, используя формулы sin(A) = a / c и cos(A) = b / c.

Основные тригонометрические функции являются основой для решения многих задач, связанных с прямоугольными треугольниками, и являются неотъемлемой частью математики и науки.

Вычисление сторон с помощью теоремы Пифагора

Таким образом, для вычисления сторон прямоугольного треугольника по теореме Пифагора необходимо знать длины двух других сторон.

Для вычисления гипотенузы (стороны, противоположной прямому углу) требуется найти квадратный корень от суммы квадратов катетов. Формула записывается следующим образом:

гипотенуза = √(a² + b²)

где a и b - длины двух катетов прямоугольного треугольника.

Для вычисления длин катетов можно использовать различные подходы. Например, можно знать длину гипотенузы и одной из сторон, и тогда можно использовать следующую формулу:

катет = √(гипотенуза² - известная сторона²)

Также можно использовать соотношение длин катетов, которое гласит, что квадрат длины одного катета равен произведению длины другого катета на длину гипотенузы. Формула выглядит следующим образом:

a² = гипотенуза * b

b = a² / гипотенуза

Используя эти методы, вы можете легко вычислить длины сторон прямоугольного треугольника с помощью теоремы Пифагора.

Использование отношений сторон треугольника

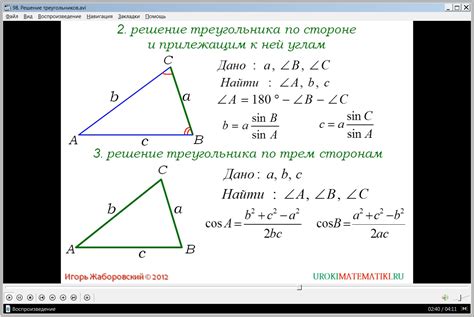
Отношения сторон прямоугольного треугольника представляют собой математические соотношения, которые позволяют находить длины его сторон, если известна длина только одной из них.

В прямоугольном треугольнике с гипотенузой (самой длинной стороной) и двумя катетами (другими двумя сторонами) справедливы следующие отношения:

• Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов: h² = a² + b²
• Тангенс угла α: отношение длины противолежащего катета к длине прилежащего катета: tgα = a/b
• Синус угла α: отношение длины противолежащего катета к длине гипотенузы: sinα = a/h
• Косинус угла α: отношение длины прилежащего катета к длине гипотенузы: cosα = b/h

Используя эти отношения, можно легко находить длины сторон прямоугольного треугольника, если известна длина хотя бы одной из них и значение угла между этой стороной и гипотенузой.

Практические примеры решения прямоугольного треугольника

Пример 1:

Пусть у нас есть прямоугольный треугольник со сторонами a = 3 и b = 4. Найдем гипотенузу (c) и площадь (S) данного треугольника.

Решение:

Используя теорему Пифагора, мы можем найти гипотенузу (c). Формула для гипотенузы:

c = √(a^2 + b^2)

Подставляя значения a = 3 и b = 4, получаем:

c = √(3^2 + 4^2) = √(9 + 16) = √25 = 5

Теперь найдем площадь (S) прямоугольного треугольника. Формула для площади:

S = (a * b) / 2

Подставляя значения a = 3 и b = 4, получаем:

S = (3 * 4) / 2 = 12 / 2 = 6

Таким образом, гипотенуза этого треугольника равна 5, а площадь равна 6.

Пример 2:

Пусть у нас есть прямоугольный треугольник со сторонами a = 5 и c = 13. Найдем сторону b и площадь (S) данного треугольника.

Решение:

Используя теорему Пифагора, мы можем найти сторону b. Формула для стороны b:

b = √(c^2 - a^2)

Подставляя значения a = 5 и c = 13, получаем:

b = √(13^2 - 5^2) = √(169 - 25) = √144 = 12

Теперь найдем площадь (S) прямоугольного треугольника. Формула для площади:

S = (a * b) / 2

Подставляя значения a = 5 и b = 12, получаем:

S = (5 * 12) / 2 = 60 / 2 = 30

Таким образом, сторона b этого треугольника равна 12, а площадь равна 30.