Дуги являются одной из основных фигур в геометрии и находят широкое применение в различных областях, включая архитектуру, инженерное дело и геодезию. Важным аспектом работы с дугами является нахождение их длины, которая может быть полезна во многих сферах жизни.
Найти длину дуги несложно, если известен радиус дуги и ее угол. Для этого можно использовать специальные формулы и методы, которые помогут решить данную задачу быстро и просто. Одной из самых популярных формул для нахождения длины дуги является формула длины окружности.
Представим себе окружность радиусом R. Вращая эту окружность на угол α, мы получим дугу, длину которой мы хотим найти. Формула длины окружности гласит: L = 2πR, где L - длина окружности, а π - математическая константа, примерное значение которой равно 3.14.
Для нахождения длины дуги с заданным углом α, вычисляется разница между длиной всей окружности и длиной дуги без угла. Таким образом, формула для нахождения длины дуги будет иметь вид: L = 2πR * (α/360), где α - угол, заданный в градусах.
Расчет дуги через радиус по основным формулам
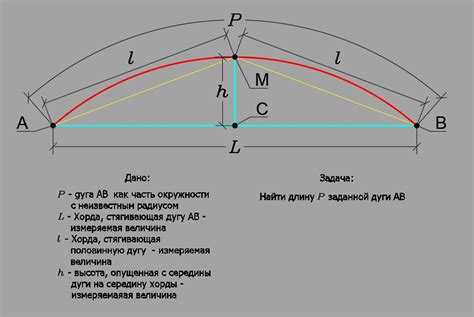
- Длина дуги равна произведению угла в радианах на радиус: L = r * theta, где L - длина дуги, r - радиус, а theta - угол в радианах.
- Длина дуги равна произведению угла в градусах на радиус, умноженное на pi/180: L = (r * theta * π)/180, где L - длина дуги, r - радиус, а theta - угол в градусах.
- Длина дуги равна произведению угла в градусах на радиус, умноженное на 2π/360: L = (r * theta * 2π)/360, где L - длина дуги, r - радиус, а theta - угол в градусах.
Выбор формулы зависит от предпочтений и требований к точности расчетов. Нужно учитывать, что для правильного применения формулы дуги через радиус необходимо знать значение радиуса и угла.
Данные формулы позволяют эффективно рассчитывать длину дуги, используя только радиус. Это удобно в различных сферах, таких как геометрия, физика, инженерия, архитектура и многих других. Знание и применение данных формул помогает более точно моделировать и строить объекты с дуговыми формами.
Использование тригонометрии для определения дуги по радиусу

Когда мы говорим о дуге, мы обычно имеем в виду дугу окружности. Окружность - это фигура, состоящая из всех точек, которые находятся на одном и том же расстоянии от определенной точки, называемой центром окружности. Радиус - это линия, соединяющая центр окружности с любой точкой на окружности.
Тригонометрические функции, такие как синус и косинус, могут помочь нам определить дугу по радиусу окружности. Для этого нам понадобится знание длины радиуса и угла, который составляет дуга с центром окружности.
Для вычисления длины дуги по радиусу можно использовать следующую формулу:
Длина дуги = радиус * угол в радианах
Здесь угол измеряется в радианах, а не в градусах. Если угол измеряется в градусах, его можно преобразовать в радианы, умножив на константу π/180.
Допустим, у нас есть окружность с радиусом 5 и углом 60 градусов. Чтобы найти длину дуги, мы сначала преобразуем угол в радианы: 60 * (π/180) = π/3. Затем мы умножаем радиус на угол в радианах: 5 * (π/3) = (5π)/3. Таким образом, длина дуги равна (5π)/3.
Использование тригонометрии для определения дуги по радиусу является важным инструментом в геометрии и других областях. Зная радиус и угол, мы можем легко вычислить длину дуги и использовать эту информацию в различных приложениях и задачах.
Применение геометрических методов для нахождения дуги через радиус
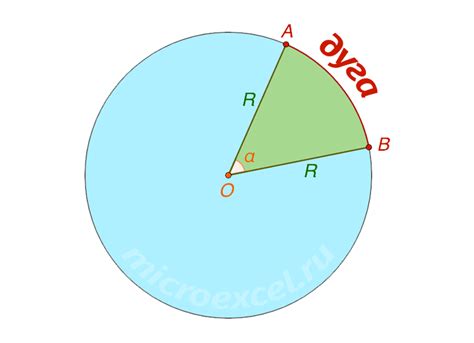
В геометрии существует несколько методов для нахождения дуги через радиус, которые могут быть полезны в различных ситуациях. Рассмотрим некоторые из них.
Один из самых простых методов для нахождения дуги через радиус - использование формулы длины окружности. Длина окружности можно найти по формуле L = 2πr, где L - длина окружности, π - математическая константа, примерно равная 3.14159, а r - радиус окружности. Зная радиус окружности, можно легко найти длину дуги.
Еще один метод заключается в использовании центрального угла. Для нахождения дуги через радиус нужно знать длину дуги и радиус окружности. Зная длину дуги, можно вычислить значение центрального угла по формуле θ = L / r, где θ - значение центрального угла, L - длина дуги, а r - радиус окружности. Зная значение центрального угла, можно легко находить дугу через радиус.
Также можно использовать тригонометрические соотношения для нахождения дуги через радиус. Если известны длина дуги и радиус окружности, то можно использовать формулу θ = L / r для нахождения значения центрального угла. Затем, применяя формулы синуса и косинуса, можно находить координаты точек на дуге через радиус.
В зависимости от конкретной задачи и доступных данных, можно выбирать наиболее подходящий метод для нахождения дуги через радиус. Знание и применение геометрических методов позволяет эффективно решать задачи связанные с окружностями и дугами.
Вычисление дуги по радиусу с помощью графического представления
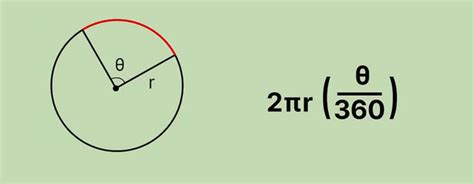
Вычисление дуги по радиусу может быть проще, если использовать графическое представление данной задачи. Графическое представление позволяет наглядно представить радиус и его влияние на форму дуги.
Для начала необходимо понять, что радиус – это линия, соединяющая центр окружности с любой точкой на ее окружности. Дугу можно представить как часть окружности между двумя точками, соединенными радиусом.
Для вычисления дуги по радиусу можно использовать следующий метод:
- Наметьте на бумаге две точки – точку А и точку В, соединенные линией. Эта линия будет представлять дугу окружности.
- Обозначьте на бумаге центр окружности точкой O.
- С помощью циркуля или компаса из центра окружности O проведите радиус до точки А и до точки В.
- Измерьте длины радиусов AO и BO. Запишите эти значения.
- Сложите длины радиусов AO и BO. Полученное значение будет длиной дуги окружности.
Наглядно, графическое представление поможет легко понять, как вычислять длину дуги по радиусу. Значение длины дуги будет зависеть от длины радиуса, а также от угла, который она охватывает.
Вычисление дуги по радиусу с помощью графического представления – это простой и эффективный способ получить точную длину дуги окружности. Благодаря понятному представлению задачи, можно легко справиться с этим математическим расчетом.
Примеры решения задачи нахождения дуги через радиус с различными значениями
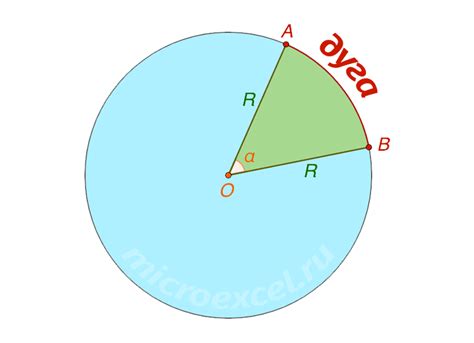
Для нахождения дуги через радиус достаточно использовать всего одну формулу:
Длина дуги = радиус х угол в радианах
Рассмотрим несколько примеров использования данной формулы:
Пример 1:
Пусть у нас есть окружность с радиусом 5 см, а угол между двумя радиусами равен 45°.
Чтобы найти длину дуги, нужно преобразовать угол из градусов в радианы: 45° × π/180 = π/4 радиан.
Теперь можно применить формулу: Длина дуги = 5 см × π/4 ≈ 3,93 см.
Пример 2:
Рассмотрим окружность с радиусом 10 м и углом между двумя радиусами, равным 60°.
Угол нужно преобразовать в радианы: 60° × π/180 = π/3 радиан.
Применяем формулу: Длина дуги = 10 м × π/3 ≈ 10,47 м.
Пример 3:
Представим окружность с радиусом 7.5 дм и углом между радиусами, равным 30°.
Преобразуем угол в радианы: 30° × π/180 = π/6 радиан.
Подставим значения в формулу: Длина дуги = 7.5 дм × π/6 ≈ 3.93 дм.
Таким образом, с помощью данной формулы можно легко находить длину дуги через радиус для различных значений радиуса и угла между радиусами окружности.
Расчет дуг через радиус с учетом сферической геометрии
При работе с радиусом дуги на сфере требуется учитывать особенности сферической геометрии. Это связано с тем, что на сфере углы и расстояния имеют другую природу, по сравнению с плоскостью. Для правильного расчета дуги через радиус на сфере необходимо применять специальные формулы.
Одной из таких формул является формула гаверсинусов, которая позволяет определить длину дуги на сфере по ее радиусу и центральному углу. Для применения данной формулы необходимо знать радиус сферы, центральный угол (в радианах) и применить следующую формулу:
S = R * θ
где:
- S - длина дуги на сфере;
- R - радиус сферы;
- θ - центральный угол (в радианах).
Применение данной формулы позволяет получить точный расчет длины дуги на сфере, учитывая сферическую геометрию. Важно помнить, что значения углов всегда должны быть выражены в радианах для корректного применения данной формулы.