Математика – это один из основных предметов в школе, который требует логического мышления и умения решать задачи. Однако, не всем ученикам легко даётся решение математических задач. В этой статье мы поделимся тремя полезными советами, которые помогут сделать задачу по математике проще и интереснее.
Первый совет – читай задачу внимательно и осознанно. Часто ученики, увидев непонятную задачу, пытаются сразу же начать решать её, не задумываясь о том, что она имеет особенности или условие, которое нужно учесть. Важно прочитать задание несколько раз, выделить ключевые слова и понять, что от тебя требуется.
Второй совет – используй логику и аналитическое мышление. Математическое мышление тренирует и развивает способность анализировать информацию, формулировать гипотезы и логически рассуждать. Перед тем, как начать решение задачи, проанализируй информацию, используй логические цепочки и думай шаг за шагом.
Третий совет – практикуйся решать разнообразные задачи. Чем больше задач ты решаешь, тем легче у тебя будет решать новые. Практика позволяет закрепить знания и навыки, а также научиться применять их в разных ситуациях. Не бойся сложных задач, они помогут тебе развиться и стать лучшим в математике.
Итак, чтобы сделать задачу по математике проще, нужно внимательно читать задание, использовать логику и аналитическое мышление, а также практиковаться в решении разнообразных задач. Следуя этим трем советам, ты достигнешь успеха в математике и сможешь справиться с любыми задачами!
Шаг 1: Понять условие
Перед тем, как приступать к решению математической задачи, важно внимательно прочитать и понять ее условие. Убедитесь, что вы правильно понимаете, что от вас требуется.
Внимательно изучите текст задачи и обратите внимание на ключевые фразы и ключевые слова.
Чтобы лучше понять задачу, выделите главные данные и важные условия, которые могут помочь вам в построении математической модели или выборе подходящей формулы.
Если вы не уверены в том, что правильно поняли условие, перечитайте его еще раз или обратитесь к учителю или однокласснику за помощью.
Совет: Используйте логику и здравый смысл для того, чтобы понять, что от вас требуется в задаче и какой математический инструмент использовать для ее решения.
Важность правильного понимания

Часто, задачи по математике могут быть формулированы в сложной и запутанной манере. В этом случае, полезно использовать выделение ключевых слов и фраз, акцентировать внимание на релевантной информации и игнорировать несущественные детали. Также, можно применить метод отработки алгоритмического мышления, разбив задачу на более мелкие шаги и последовательно анализируя каждый из них.
При правильном понимании задачи, вы можете:
- Избежать ошибок: Задачи по математике требуют точности и логического мышления. Правильное понимание условий задачи поможет избежать ошибок в решении и ответах, что может быть критически важным в ситуациях, где неправильное решение может привести к негативным последствиям.
- Разработать эффективную стратегию: Правильно поняв задачу, вы сможете разработать оптимальную стратегию решения. Выделение ключевых аспектов и понимание логики задачи поможет сократить время и усилия, затрачиваемые на ее решение.
- Применить правильные концепции и методы: В понимании задачи заключено понимание того, какие концепции и методы следует использовать для ее решения. Это позволит сосредоточиться на соответствующих математических принципах и подходах, что повысит вероятность правильного решения.
В заключении, правильное понимание задачи является неотъемлемой частью успешного решения математических проблем. Посвящение времени на тщательное изучение условий задачи и выделение ключевой информации поможет избежать ошибок, разработать эффективную стратегию решения и применить правильные концепции и методы. Этот подход сделает процесс решения задач более легким и успешным.
Шаг 2: Разбить на подзадачи

Когда вы столкнулись с сложной математической задачей, необходимо разбить ее на более простые подзадачи. Это поможет вам лучше понять задачу и найти путь к ее решению. Вот несколько полезных советов, как разбить задачу на подзадачи:
- Внимательно прочитайте задачу и выделите ключевые слова или фразы. Они могут указать на основные компоненты задачи, с которыми вам нужно будет работать.
- Разбейте задачу на несколько этапов или шагов. Это поможет вам логически структурировать задачу и разделить ее на более мелкие части.
- Для каждого этапа определите необходимые математические операции или формулы. Это позволит вам определить, какие знания или навыки вам потребуются для решения каждой подзадачи.
Например, рассмотрим задачу: "Вам нужно рассчитать площадь треугольника. Известны длины всех трех сторон: 5 см, 6 см и 7 см".
- Ключевые слова: площадь треугольника, длины сторон.
- Этапы: найти полупериметр, использовать формулу Герона для вычисления площади.
- Математические операции: сложение, умножение, вычисление квадратного корня.
Разбивая задачу на подзадачи, вы сможете логически структурировать свои мысли и легче решать каждую подзадачу по отдельности. Это позволит вам сделать задачу по математике более управляемой и понятной.
Полезный метод декомпозиции
Одним из ключевых преимуществ декомпозиции является возможность сосредоточиться на меньших задачах, что делает их более понятными и решаемыми. При декомпозиции задачи, вы можете использовать различные стратегии, такие как разделение задачи на подзадачи с использованием таблицы.
Ниже приведен пример таблицы декомпозиции задачи на поиск площади прямоугольника:
| Подзадача | Решение |
|---|---|
| Найти длину стороны А | Известны ширина и площадь |
| Найти длину стороны В | Известны ширина и площадь |
| Найти площадь | Длины сторон А и В |
Таким образом, декомпозиция позволяет разбить сложную задачу на более простые и понятные подзадачи, что делает решение математических задач более эффективным и удобным.
Шаг 3: Выбрать подходящий метод решения

После того как вы поняли условие задачи и разобрались с известными данными, настало время выбрать подходящий метод решения. В математике существует множество различных методов, и ваша задача заключается в том, чтобы выбрать тот, который наилучшим образом подходит для данной задачи.
Один из основных способов выбора метода состоит в том, чтобы проанализировать данные, данную формулу желаемого результата и запрошенное решение. Если задача требует вычислений или использования известных формул, вам может потребоваться применить алгебру или геометрию. Если задача связана с возрастающими или убывающими числовыми последовательностями, вам может потребоваться использовать арифметическую или геометрическую прогрессию.
Пример 1: Задача на алгебру, требующая использование формулы.
Если вам нужно вычислить площадь прямоугольника, для этой задачи можно использовать формулу S = a * b, где S - площадь, а и b - длины сторон прямоугольника. Вам нужно известнять лишь значения длин сторон, чтобы применить данную формулу и получить решение.
Примечание: При выборе подходящего метода решения следует учитывать свои знания и навыки в соответствующей области математики.
Применение алгоритма или формулы

Перед применением алгоритма или формулы необходимо внимательно прочитать условие задачи и определить, какая формула или алгоритм может быть применен для ее решения. Иногда это может потребовать некоторого творческого подхода и анализа ситуации.
При выборе формулы или алгоритма важно обратить внимание на указанные в задаче величины и значения параметров. Они могут быть необходимы для корректного применения формулы или алгоритма.
После выбора формулы или алгоритма следует записать его в виде математического выражения или последовательности действий. При этом важно соблюдать порядок выполнения операций и использовать правильные математические обозначения.
Затем можно приступать к расчетам, подставляя в формулу или алгоритм известные величины и параметры. Результаты расчетов следует анализировать, проверять и округлять, если это необходимо.
Важно помнить, что при применении алгоритма или формулы возможны различные подходы и способы решения задач. Более опытные математики могут использовать более сложные формулы и алгоритмы для решения задач.
Применение алгоритма или формулы - это один из ключевых навыков, которые развиваются при изучении математики. Он позволяет применять математические знания на практике и решать различные задачи.
Пример 1: Вычисление площади треугольника
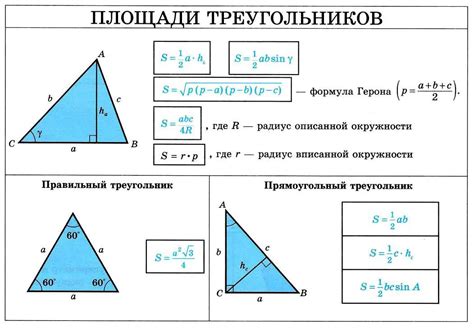
Чтобы вычислить площадь треугольника, необходимо знать длину основания и высоту треугольника. Давайте рассмотрим пример:
У нас есть треугольник ABC, где сторона AB является основанием, а высота треугольника обозначается точкой H и проходит через вершину C и перпендикулярна основанию AB. Помните, что высота всегда перпендикулярна к основанию и проходит через ее конец.
Дано: длина основания AB = 10 см и высота треугольника HС = 7 см.
Вычисление площади треугольника проводится по формуле: S = (1/2) * AB * HC.
Подставляем известные значения в формулу:
S = (1/2) * 10 см * 7 см = 35 см².
Таким образом, площадь треугольника ABC равна 35 квадратным сантиметрам.
Исходные данные и последовательность действий

Перед тем, как приступить к решению задач по математике, необходимо внимательно ознакомиться с исходными данными и составить последовательность действий, которая поможет нам достичь нужного результата. В этом разделе мы рассмотрим, как правильно работать с этапом формулировки исходных данных и составления плана действий.
1. Внимательно прочитайте условие задачи и обратите внимание на ключевые слова и фразы. Они помогут вам понять, что требуется решить. Обычно задачи содержат информацию о количестве исходных данных, известных величинах, условиях и требуемом результате.
2. Создайте таблицу, где в первом столбце указаны исходные данные, а во втором - значения, получаемые в результате решения задачи. Это поможет вам более наглядно организовать информацию и не пропустить какие-либо детали.
| Исходные данные | Значения |
|---|---|
| Количество яблок | - |
| Цена одного яблока | - |
| Скидка | - |
| Сумма | - |
3. Последовательно выполните необходимые действия для решения задачи. Это может включать в себя арифметические операции (сложение, вычитание, умножение, деление), использование формул и т.д. Опишите каждое действие подходящими фразами или формулами, чтобы у вас было четкое представление о том, что нужно сделать.
Например, если задача состоит в подсчете общей стоимости покупки, то последовательность действий может выглядеть следующим образом:
1. Умножьте количество яблок на цену одного яблока.
2. Вычтите скидку из полученной суммы.
3. Результатом будет общая стоимость покупки.
Используя эти советы и придерживаясь последовательности действий, вы сможете эффективно решать задачи по математике и достигать желаемых результатов.
Пример 2: Расчет процента скидки
Рассмотрим пример расчета процента скидки. Предположим, что товар стоит 5000 рублей, а на него действует скидка в размере 20%. Какой будет цена со скидкой?
Для решения этой задачи нужно умножить стоимость товара на процент скидки и разделить на 100:
Стоимость со скидкой = 5000 * 20 / 100 = 1000
Таким образом, цена товара со скидкой составит 1000 рублей.