В математике корень из рационального числа – это такое число, при возведении в квадрат которого получается исходное рациональное число. На первый взгляд может показаться, что нахождение корня из рационального числа является сложной задачей. Однако, существуют эффективные методы расчета, которые позволяют получить точный результат.
Один из основных методов нахождения корня из рационального числа – это метод итераций, который использует последовательность приближений для достижения желаемого результата. В основе этого метода лежит идея последовательного уточнения ответа до тех пор, пока не будет достигнута нужная точность. Этот метод легко применить в программировании и позволяет получить корень с любой степенью точности.
Другим эффективным методом нахождения корня из рационального числа является метод Ньютона, который использует тангенс угла наклона касательной к графику функции. Этот метод основан на итерационной последовательности и обеспечивает быструю сходимость к точному значению корня. Однако для его применения необходимо знание производной функции, что может быть сложным в некоторых случаях.
В обоих методах нахождения корня из рационального числа важно учитывать возможность ошибки вычислений и выбирать подходящий уровень точности. Также следует помнить, что не все рациональные числа имеют точные корни. В некоторых случаях значение корня может быть иррациональным числом или представлять бесконечную десятичную дробь.
Итак, нахождение корня из рационального числа требует применения соответствующих методов и учета особенностей задачи. Следуя подробной инструкции и использованию эффективных методов, можно достичь точного результата и получить ответ с требуемой степенью точности.
Подробная инструкция по поиску корня из рационального числа

Шаг 2: Проверьте, является ли индекс корня (степень) рациональным числом. Степень также должна быть представлена в виде дроби.
Примечание: Если числа не являются рациональными, то вы не сможете найти точное значение корня. В таком случае вам придется использовать численные методы для приближенного вычисления.
Шаг 3: Разложите число на простые множители. Если число является полным квадратом или полным кубом, то вы сможете найти точное значение корня.
Шаг 4: Используйте правила алгебры, чтобы вычислить корень. Если индекс корня является четным числом, то результат может быть положительным или отрицательным. Если индекс корня является нечетным числом, то результат всегда будет положительным.
Шаг 5: Проверьте свое решение путем возведения найденного корня в степень, равную индексу, и убедитесь, что результат равен исходному числу.
Примечание: Если вам требуется приближенное значение корня, вы можете использовать различные методы, такие как метод Ньютона или метод деления отрезка пополам.
Методы упрощения и нахождения корня
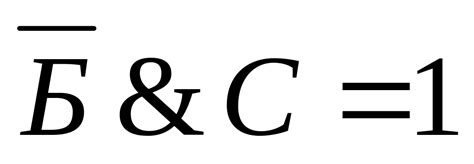
Нахождение корня из рационального числа может быть достаточно сложной задачей, но существуют эффективные методы и алгоритмы, которые позволяют упростить этот процесс. В данном разделе мы рассмотрим некоторые из них.
- Методы поиска приближенного значения:
- Метод деления отрезка пополам: данный метод заключается в последовательном делении отрезка, содержащего искомый корень, пополам до достижения достаточно маленькой разницы между значениями деления. Это приближенное значение и будет являться корнем рационального числа.
- Метод Ньютона: данный метод основан на использовании производной функции и последовательном приближении к корню путем пересчета уравнения с использованием формулы Ньютона.
- Метод разложения на множители: данный метод заключается в разложении исходного рационального числа на простые множители. Затем корни каждого из множителей находятся независимо друг от друга, а их значения комбинируются для получения значения корня исходного числа.
- Метод приведения квадратного корня к целому числу: данный метод применяется при нахождении корня из числа, которое является полным квадратом. В этом случае корень может быть найден путем извлечения из числа его целой части.
Выбор конкретного метода зависит от сложности исходного рационального числа, а также требуемой точности результата. Экспериментирование с различными методами и алгоритмами может помочь в выборе оптимального подхода к нахождению корня.
Эффективные способы вычисления корня

1. Метод Ньютона-Рафсона
Метод Ньютона-Рафсона является одним из классических алгоритмов для вычисления корня. Он основан на итерационном процессе и решает уравнение f(x) = 0, где f(x) - функция, корнем которой является искомое число. Алгоритм состоит из последовательности шагов, которые вычисляются до достижения заданной точности.
2. Метод деления отрезка пополам
Метод деления отрезка пополам основан на принципе двоичного поиска. Этот метод применяется для нахождения корня из уравнения f(x) = 0 на заданном отрезке [a, b]. Используя свойства функции f(x), можно сузить интервал поиска до достижения заданной точности.
3. Итерационный метод Бабилюка-Турчина
Итерационный метод Бабилюка-Турчина представляет собой комбинацию методов Ньютона-Рафсона и деления отрезка пополам. Этот метод обладает высокой скоростью сходимости и может быть использован для эффективного вычисления корня.
4. Методы специальных функций
Существуют специальные функции, которые позволяют вычислить корень из рационального числа без использования итерационных алгоритмов. Такие функции используются в математическом программном обеспечении и обладают высокой точностью вычислений.
| Метод | Описание |
|---|---|
| Метод Ньютона-Рафсона | Итерационный метод для решения уравнения f(x) = 0 |
| Метод деления отрезка пополам | Метод двоичного поиска корня на заданном отрезке |
| Итерационный метод Бабилюка-Турчина | Комбинированный метод Ньютона-Рафсона и деления отрезка пополам |
| Методы специальных функций | Использование специальных функций для точного вычисления корня |
Выбор способа вычисления корня зависит от поставленной задачи, требуемой точности и доступных вычислительных ресурсов. Независимо от выбранного метода, важно проводить проверку полученного результата на соответствие заданной точности и корректность вычислений. Используя эффективные способы вычисления корня, можно повысить точность и скорость работы алгоритмов в различных областях науки и техники.